ДЗ_Логистика_6. Название кафедры) Контрольное задание по дисциплине вариант (тема) N6
 Скачать 154 Kb. Скачать 154 Kb.
|
|
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ» Институт заочного обучения Институт______________________________ (название института) Кафедра____________________________________ (название кафедры) Контрольное задание по дисциплине_____________________________ вариант (тема) N6 Выполнил(а) студент(ка) заочной формы обучения специальности_____________________________ специализации_____________________________ _____курс________группы___________________ № студенческого билета (зачетной книжки)_____________ _____________ _________________ (подпись) (инициалы, фамилия) Проверил преподаватель ______________________ _________________ ____________________ (ученая степень, звание) (подпись) (инициалы, фамилия) Москва 2007 Груз находится в пункте Ц – 300 коробок. Используется автомобиль грузоподъемностью 150 коробок. Необходимо организовать перевозку между пунктами потребления с минимальным пробегом подвижного состава.     2 Ц 2 Ц      1     M M   G G    U U N N  Z    K K W WСхема 1. Размещение пунктов потребления и транспортные связи между ними. Таблица 1 Объёмы продукции завозимые в пункты потребления
Таблица 2 Исходные данные о расстояниях между пунктами потребления сети развоза мелких партий груза по разным вариантам заданий
Расчета развязочных маршрутов. Потребность в мелкопартионных поставках продукции потребителям с баз и складов систематически возрастает, поэтому организация маршрутов на отгрузку потребителям мелких партий груза имеет большое значение. Основные обозначения методики расчета развязочных маршрутов. Гi – населенный пункт (пункт потребления); i = A-Z, 0-9; Ц – распределительный центр (или склад, начальный пункт); q – потребность заказчиков в единицах объема груза (стандартная коробка); Q – грузоподъемность транспортного средства; Сij – стоимость перевозки (расстояние). Формулировка задачи Имеются пункты потребления Гi (i = A-Z, 0-9). Груз необходимо развести из начального пункта (распределительного центра – Ц) во все остальные пункты, т.е. к потребителям. Потребность пунктов потребления в единицах объема груза составляет: qA, qB...qZ; q0...q9 В начальном пункте (распределительном центре – Ц) имеются транспортные средства грузоподъемностью: Q1, Q2...Qd. Для каждой пары пунктов (Гi, Гj) определяют стоимость перевозки Cij ≥ 0. Требуется найти m-количество замкнутых путей l1, l2...lm из единственной общей точки (распределительного центра – Ц) так, чтобы выполнялось условие: 2.Методика составления рациональных маршрутов при расчетах вручную Смотрите в качестве исходных данных таблицу 3 о заявках потребителей продукции и схему 2 о размещении пунктов потребления и расстояниях между ними. Таблица 3 Заявки потребителей продукции на один день
Груз находится в пункте Ц – 300 коробок, используется автомобиль грузоподъемностью 150 коробок. Необходимо организовать перевозку между пунктами с минимальным пробегом подвижного состава.  4,2 4,2  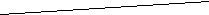  3,5 Ц 3,5 Ц 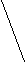 1 2 1 2 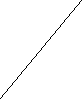 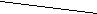 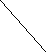 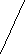 4,8 2,7 4,8 2,74,3 2.1 M 4,2  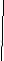 2,8 2,8  G G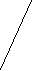   U 5,1 3,0 U 5,1 3,0  3,8 2,8 3,8 2,8 Z 3,3 Z 3,3 5,3 N 5,3 N    4,1 2,2 4,1 2,2W 7,2 K  Схема 2. Размещение пунктов потребления и расстояния между ними РЕШЕНИЕ: (состоит из нескольких этапов) I этап – строим кратчайшую сеть, связывающую все пункты без замкнутых контуров. (см. рис.1. Кратчайшая связывающая сеть (“минимальное дерево”).   47 кор. 47 кор.Ц   10 кор. 2,1 U 10 кор. 2,1 U  2,7 2,7 2 2M 50 кор.   3,5 3,5  20 кор 3,0 20 кор 3,0 1 1  N 35 кор. N 35 кор. 2,8 2,2 2,8     15 кор. 60 кор. 10 кор. 15 кор. 60 кор. 10 кор.Z 4,1 W 7,2 K G   53 кор. 53 кор.Рис.1 Кратчайшая связывающая потребителей сеть («минимальное дерево») Затем, по каждой ветви сети, начиная с пункта наиболее удаленного от распределительного центра, группируем пункты по маршрутам с учетом:
Исходя из заданной грузоподъемности собственного транспортного средства – 120 коробок и количества развозимого груза, все пункты потребления можно сгруппировать в 2 группы (таблица 4) Таблица 4 Распределение пунктов потребления по группам (маршрутам)
Сгруппировав пункты по группам, переходим ко второму этапу расчетов. II Этап. Определяем рациональный порядок (маршрут) объезда пунктов каждой группы пунктов. Для этого строим таблицу-матрицу, в которой по диагонали размещаем пункты, включаемые в маршрут, и начальный пункт (Ц), а в соответствующих клетках - кратчайшие расстояния между ними (см. табл. 5). Таблица 5 Таблица-матрица для маршрута 1.
Начальный маршрут строим для трех пунктов матрицы Ц-W-K-Ц, имеющих наибольшее значение суммы расстояний в итоговой строке. соответственно, 46,8 46,6 49, т.е. Ц - K - W - Ц Для включения последующих пунктов вsбираем из оставшихся пункт, имеющий наибольшую сумму, например, N (сумма 42,8) и решаем между какими пунктами его следует включать, т.е. между (Ц-K) −1 пара; (K-W) −2 пара; (W-Ц) −3 пара Поэтому, для каждой пары пунктов необходимо найти величину приращения маршрута ∆kp по формуле: ∆kp=Cki+Cip-Ckp; где: С – расстояние, км; k – индекс первого пункта из пары; i – индекс включаемого пункта; р – индекс второго пункта из пары. а) При включении пункта N между первой парой пунктов Ц и K определяем размер приращения цk, исходя из условия: i = N; k = Ц; p = K. цk = Cцn + Сnk - Сцk, подставляя значения из таблицы 2 находим: цk= 5,7 + 2,2 - 7,5 = 0,7 б) Таким же образом определим приращение kw, если пункт N включить между пунктами K и W: kw = Сkn + Cnw – Ckw = 2,2 + 9,4 - 7,2 = 14,4 в) Приращение WЦ, если пункт N включить между пунктами W и Ц wц = Сwn + Cnц – Сwц = 9,4 + 5,7 - 11,6 = 4,5 Из полученных значений выбираем минимальное приращение цk = 0,7, тогда маршрут Ц – K – W - Ц преобразуется в маршрут Ц – N – K – W – Ц. Используя этот метод и формулу приращения, определяем между какими пунктами надо расположить пункты 1,2 и Z. Начнем с пункта Z,т.к. размер суммы в итоговой таблице 42,9>41,9>37,6 цn = Cцz + Сzn – Cцn = 10,1 + 8,9 – 5,7 = 13,3; nk = Сnz + Czk – Cnk = 8,9 + 11,1– 2,2 = 17,8; kw= Сkz + Czw – Ckw = 11,1 + 4,1 – 7,2 = 8,0 wц = Сwz + Сzц – Сwц = 4,1 + 10,1 – 11,6 = 2,6 min; Пункт Z должен быть между пунктами W и Z. Тогда маршрут получит вид: Ц – N – K – W –Z - Ц. Определяемся с пунктом 1 цn= Cц1 + C1n – Cцn = 7,7 + 9,4 – 5,7 = 11,4 nk= Cn1 + C1k – Cnk = 9,4 + 11,6 – 2,2 = 18,8 kw= Ck1 + C1w – Ckw = 11,6 + 6,9 – 7,2=11,3 wz= Cw1 + C1z – Cwz = 6,9 + 2,8 – 4,1 = 5,6 zц= Cz1 + C1ц – Czц = 2,8+ 7,7 – 10,1 = 0,4min; Пункт 1 должен быть между пунктами Z и Ц. Тогда маршрут получит вид: Ц – N – K – W –Z – 1 - Ц. Определяемся с пунктом 2 1ц= C12 + C2ц – C1ц = 3,5+ 4,2 – 7,7 = 0min; Поскольку матрица симметричная и 1w=0, то дальнейшие расчеты можно не продолжать, т.к. меньшее значение, чем 0, получено быть не может. Поэтому пункт 2 должен быть между пунктами 1 и Ц. таким образом, окончательный порядок движения по маршруту:Ц – N – K – W –Z – 1 – 2 - Ц.   2 4,2 Ц    3,5 5,7 3,5 5,7     2,8 4,1 7,2 2,2 2,8 4,1 7,2 2,2    1 Z W K N 1 Z W K N L = 29,7 км Рис.2 Порядок движения по маршруту 1. Таким же методом определяется кратчайший путь объезда пунктов по маршруту 2. Определяем рациональный порядок объезда пунктов маршрута 2. Для этого формируется таблица 5, таблица-матрица маршрута 2, в которой по диагонали размещаются пункты, включаемые в маршрут 2 и начальный пункт Ц, а в соответствующих клетках кратчайшие расстояния между ними. Начальный маршрут строим для трех пунктов матрицы: Ц – U – G – Ц, имеющих наибольшие значения в итоговой строке(Ц отправной пункт). Для включения последующего пункта М решаем между какими пунктами его следует включать: Ц – U, U – G или G - Ц Поэтому для каждой пары пунктов необходимо найти величину приращения маршрута. Таблица 6 Таблица-матрица для маршрута 2.
а) Включение пункта М между парой пунктов Ц и U: цu= Сцм + Смu – Сцu = 2,7 + 6,9 – 6,3 = 3,3 ug= Сuм + Смg – Сug = 6,9 + 5,8 – 7,9 = 4,8 gц= Сgм + Смц – Сgц = 5,8 + 2,7 – 4,2 = 4,3 Пункт M следует включить между пунктами Ц и K, То есть маршрут Ц – U – G – Ц превращается в маршрут Ц – М – U – G – Ц. Результаты расчета В итоге получили 2 маршрута, порядок движения по которым представлен в графическом виде на рис 2 (I маршрут Ц – U – W – Z – 1 – 2 - Ц) и на рис. 3 маршрут 2: Ц – М – U – G – Ц.   4,2 4,2 G Ц G Ц  7,9 7,92,7   6,9 6,9  U M U ML = 21,7 км Рис.3 Порядок движения по маршруту 2. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
