Нелинейное программирование
 Скачать 220.65 Kb. Скачать 220.65 Kb.
|
3. Условия Куна-ТаккераВ предыдущем разделе было установлено, что множители Лагранжа можно использовать при построении критериев оптимальности для задач оптимизации с ограничениями в виде равенств. Кун и Таккер обобщили этот подход на случай общей задачи нелинейного программирования с ограничениями, как в виде равенств, так и в виде неравенств. Рассмотрим следующую общую задачу нелинейного программирования: минимизировать 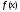 (0) (0)при ограничениях 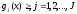 (1) (1)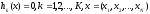 (2) (2)Определение: Ограничение в виде неравенства 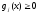 называется активным, или связывающим, в точке называется активным, или связывающим, в точке 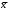 , если , если 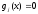 , и неактивным, или несвязывающим, если , и неактивным, или несвязывающим, если 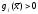 Если существует возможность обнаружить ограничения, которые неактивны в точке оптимума, до непосредственного решения задачи, то эти ограничения можно исключить из модели и тем самым уменьшить ее размеры. Основная трудность заключается при этом в идентификации неактивных ограничений, предшествующей решению задачи. Кун и Таккер построили необходимые и достаточные условия оптимальности для задач нелинейного программирования, исходя из предположения о дифференцируемости функций 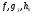 . Эти условия оптимальности, широко известные как условия Куна—Таккера, можно сформулировать в виде задачи нахождения решения некоторой системы нелинейных уравнений и неравенств, или, как иногда говорят, задачи Куна—Таккера. . Эти условия оптимальности, широко известные как условия Куна—Таккера, можно сформулировать в виде задачи нахождения решения некоторой системы нелинейных уравнений и неравенств, или, как иногда говорят, задачи Куна—Таккера.3.1. Условия Куна—Таккера и задача Куна—ТаккераНайти векторы 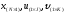 ,удовлетворяющие следующим условиям ,удовлетворяющие следующим условиям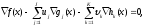 (3) (3)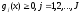 (4) (4)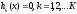 (5) (5)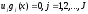 (6) (6)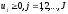 (7) (7)Прежде всего проиллюстрируем условия Куна — Таккера на примере. Пример 3 Минимизировать 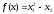 при ограничениях 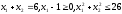 Решение. Записав данную задачу в виде задачи нелинейного программирования (0)-(2), получим 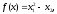 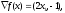 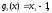 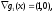 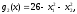 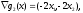 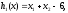 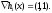 Уравнение (3), входящее в состав условий Куна—Таккера, принимает следующий вид: 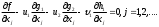 откуда 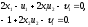 Неравенства (4) и уравнения (5) задачи Куна — Таккера в данном случае записываются в виде 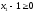 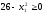 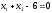 Уравнения (5.16), известные как условие дополняющей нежесткости, принимают вид 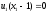 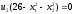 Заметим, что на переменные 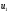 и и 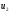 накладывается требование неотрицательности, тогда как ограничение на знак накладывается требование неотрицательности, тогда как ограничение на знак 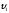 отсутствует. отсутствует.Таким образом, этой задачи условия Куна—Танкера записываются в следующем виде: 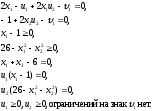 |
