Нелинейное программирование
 Скачать 220.65 Kb. Скачать 220.65 Kb.
|
4.1.1. Метод поиска по симплексу(S2 -метод)Первые попытки решения оптимизационных задач без ограничений на основе прямого поиска связаны с использованием одномерных методов оптимизации. Как правило, при реализации таких методов допустимая область определения показателя качества функционирования системы (целевой функции) заменяется дискретным множеством (решеткой) точек пространства управляемых переменных, а затем используются различные стратегии уменьшения области, которая содержит решение задачи. Часто эта процедура оказывается эквивалентной равномерному поиску в узлах решетки и, следовательно, непригодной для решения задач с числом переменных, превышающим 2. Более полезная идея заключается в выборе базовой точки и оценивании значений целевой функции в точках, окружающих базовую точку. Например, при решении задачи с двумя переменными можно воспользоваться квадратным образцом, изображенным на рис.2  Рис 2. Квадратный образец (частный случай кубического образца) Затем «наилучшая» из пяти исследуемых точек выбирается в качестве следующей базовой точки, вокруг которой строится аналогичный образец. Если ни одна из угловых точек не имеет преимущества перед базовой, размеры образца следует уменьшить, после чего продолжить поиск. Этот тип эволюционной оптимизации был использован Боксом и другими исследователями для анализа функционирования промышленных предприятий, когда эффект варьирования значений переменных, описывающих производственные процессы, измеряется с ошибкой. В задачах большой размерности вычисление значений целевой функции проводится во всех вершинах, а также в центре тяжести гиперкуба (гиперкуб – куб в n-мерном евклидовом пространстве, т.е. множество S={x=( 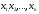 ) )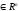 | | 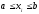 } , где а и b – заданные числа ) , т. е. в точках так называемого кубического образца. Если количество переменных (размерность пространства, в котором ведется поиск) равно n, то поиск по кубическому образцу требует } , где а и b – заданные числа ) , т. е. в точках так называемого кубического образца. Если количество переменных (размерность пространства, в котором ведется поиск) равно n, то поиск по кубическому образцу требует  +1 вычислений значения функций для одного образца. При увеличении размерности задачи необходимое количество вычислений значения целевой функции возрастает чрезвычайно быстро. Таким образом, несмотря на логическую простоту поиска по кубическому образцу, возникает необходимость использования более эффективных методов прямого поиска для решения возникающих на практике задач оптимизации. +1 вычислений значения функций для одного образца. При увеличении размерности задачи необходимое количество вычислений значения целевой функции возрастает чрезвычайно быстро. Таким образом, несмотря на логическую простоту поиска по кубическому образцу, возникает необходимость использования более эффективных методов прямого поиска для решения возникающих на практике задач оптимизации.Одна из вызывающих особый интерес стратегий поиска положена в основу метода поиска по симплексу, предложенного Спендли, Хекстом и Химсвортом. Следует отметить, что указанный метод и другие подобные методы не имеют отношения к симплекс-методу линейного программирования, а сходство названий носит случайный характер. Процедура симплексного поиска Спендли, Хекста и Химсворта базируется на том, что экспериментальным образцом, содержащим наименьшее количество точек, является регулярный симплекс. Регулярный симплекс в n-мерном пространстве представляет собой многогранник, образованный n+1 равностоящими друг от друга точками-вершинами. Например, в случае двух переменных симплексом является равносторонний треугольник; в трехмерном пространстве симплекс представляет собой тетраэдр. В алгоритме симплексного поиска используется важное свойство симплексов, согласно которому новый симплекс можно построить на любой грани начального симплекса путем переноса выбранной вершины на надлежащее расстояние вдоль прямой, проведенной через центр тяжести остальных вершин начального симплекса. Полученная таким образом точка является вершиной нового симплекса, а выбранная при построении вершина начального симплекса исключается. Нетрудно видеть, что при переходе к новому симплексу требуется одно вычисление значения целевой функции. Рис 3 иллюстрирует процесс построения нового симплекса на плоскости. 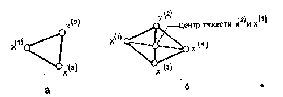 Рис.3.Построение нового симплекса. а – начальный симплекс 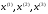 б – новый симплекс 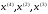 Работа алгоритма симплексного поиска начинается с построения регулярного симплекса в пространстве независимых переменных и оценивания значений целевой функции в каждой из вершин симплекса. При этом определяется вершина, которой соответствует наибольшее значение целевой функции. Затем найденная вершина проецируется через центр тяжести остальных вершин симплекса в новую точку, которая используется в качестве вершины нового симплекса. Если функция убывает достаточно плавно, итерации продолжаются до тех пор, пока либо не будет накрыта точка минимума, либо не начнется циклическое движение по двум или более симплексам. В таких ситуациях можно воспользоваться следующими тремя правилами. Правило 1. «Накрытие» точки минимума Если вершина, которой соответствует наибольшее значение целевой функции, построена на предыдущей итерации, то вместо нее берется вершина, которой соответствует следующее по величине значение целевой функции. Правило 2. Циклическое движение Если некоторая вершина симплекса не исключается на протяжении более чем М итераций, то необходимо уменьшить размеры симплекса с помощью коэффициента редукции и построить новый симплекс, выбрав в качестве базовой точку, которой соответствует минимальное значение целевой функции. Спендли, Хекст и Химс-ворт предложили вычислять М по формуле M=1,65n+0,05 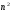 где n — размерность задачи, а М округляется до ближайшего целого числа. Для применения данного правила требуется установить величину коэффициента редукции. Правило 3. Критерий окончания поиска Поиск завершается, когда или размеры симплекса, или разности между значениями функции в вершинах становятся достаточно малыми. Чтобы можно было применять эти правила, необходимо задать величину параметра окончания поиска. Реализация изучаемого алгоритма основана на вычислениях двух типов: (1) построении регулярного симплекса при заданных базовой точке и масштабном множителе и (2) расчете координат отраженной точки. Построение симплекса является достаточно простой процедурой, так как из элементарной геометрии известно, что при заданных начальной (базовой) точке 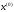 и масштабном множителе и масштабном множителе  координаты остальных n вершин симплекса в n-мерном пространстве вычисляются по формуле координаты остальных n вершин симплекса в n-мерном пространстве вычисляются по формуле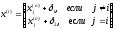 (7) (7)для i и j=1,2,3,…,n Приращения 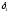 и и 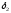 , зависящие только от n и выбранного масштабного множителя , зависящие только от n и выбранного масштабного множителя , определяются по формулам , определяются по формулам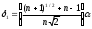 (8) (8)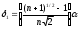 (9) (9) Заметим, что величина масштабного множителя  выбирается исследователем, исходя из характеристик решаемой задачи. При выбирается исследователем, исходя из характеристик решаемой задачи. При  =1 ребра регулярного симплекса имеют единичную длину. Вычисления второго типа, связанные с отражением относительно центра тяжести, также представляют несложную процедуру. Пусть =1 ребра регулярного симплекса имеют единичную длину. Вычисления второго типа, связанные с отражением относительно центра тяжести, также представляют несложную процедуру. Пусть  — точка, подлежащая отражению. Центр тяжести остальных n точек расположен в точке — точка, подлежащая отражению. Центр тяжести остальных n точек расположен в точке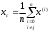 (10) (10)Все точки прямой, проходящей через  и хс, задаются формулой и хс, задаются формулой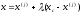 (11) (11)При 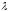 =0 получаем исходную точку =0 получаем исходную точку 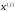 , тогда как значение , тогда как значение 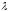 =1 соответствует центру тяжести хс. Для того чтобы построенный симплекс обладал свойством регулярности, отражение должно быть симметричным. Следовательно, новая вершина получается при =1 соответствует центру тяжести хс. Для того чтобы построенный симплекс обладал свойством регулярности, отражение должно быть симметричным. Следовательно, новая вершина получается при 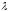 =2. Таким образом, =2. Таким образом,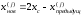 (12) (12)Проиллюстрируем вычислительную схему метода следующим примером. Пример 5. Вычисления в соответствии с методом поиска по симплексу Минимизировать f(x)= 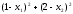 Решение. Для построения исходного симплекса требуется задать начальную точку и масштабный множитель. Пусть x 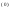 = =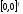 и и  =2. Тогда =2. Тогда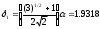 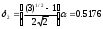 Используя эти два параметра, вычислим координаты двух остальных вершин симплекса: 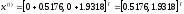 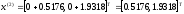 которым соответствуют значения целевой функции, равные 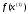 =0,2374 и =0,2374 и 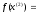 3,0658. Так как 3,0658. Так как 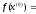 5, необходимо отразить точку 5, необходимо отразить точку 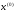 относительно центра тяжести двух остальных вершин симплекса относительно центра тяжести двух остальных вершин симплекса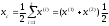 Используя формулу (12), получаем 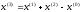 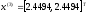 В полученной точке 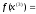 2,3027, т. е. наблюдается уменьшение целевой функции. Новый симплекс образован точками 2,3027, т. е. наблюдается уменьшение целевой функции. Новый симплекс образован точками 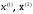 и и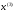 . В соответствии с алгоритмом следует отразить точку х(2), которой соответствует наибольшее значение целевой функции, относительно центра тяжести точек . В соответствии с алгоритмом следует отразить точку х(2), которой соответствует наибольшее значение целевой функции, относительно центра тяжести точек 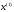 и х(3). Итерации продолжаются до тех пор, пока не потребуется применение правил 1, 2 и 3, которые были сформулированы выше. и х(3). Итерации продолжаются до тех пор, пока не потребуется применение правил 1, 2 и 3, которые были сформулированы выше.Изложенный выше алгоритм 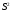 - метода имеет несколько очевидных преимуществ. - метода имеет несколько очевидных преимуществ.1. Расчеты и логическая структура метода отличаются сравнительной простотой, и, следовательно, соответствующая программа для ЭВМ оказывается относительно короткой. 2. Уровень требований к объему памяти ЭВМ невысокий, массив имеет размерность (n+1, n+2). 3. Используется сравнительно небольшое число заранее установленных параметров: масштабный множитель  , коэффициент уменьшения множителя , коэффициент уменьшения множителя  (если применяется правило 2) и параметры окончания поиска. (если применяется правило 2) и параметры окончания поиска.4. Алгоритм оказывается эффективным даже в тех случаях, когда ошибка вычисления значений целевой функции велика, поскольку при его реализации оперируют наибольшими значениями функции в вершинах, а не наименьшими. Перечисленные факторы характеризуют метод поиска по симплексу как весьма полезный при проведении вычислений в реальном времени. Алгоритм обладает также рядом существенных недостатков. 1. Не исключено возникновение трудностей, связанных с масштабированием, поскольку все координаты вершин симплекса зависят от одного и того же масштабного множителя  . Чтобы обойти трудности такого рода, в практических задачах следует промасштабировать все переменные с тем, чтобы их значения были сравнимыми по величине. . Чтобы обойти трудности такого рода, в практических задачах следует промасштабировать все переменные с тем, чтобы их значения были сравнимыми по величине.2. Алгоритм работает слишком медленно, так как полученная на предыдущих итерациях информация не используется для ускорения поиска. 3. Не существует простого способа расширения симплекса, не требующего пересчета значений целевой функции во всех точках образца. Таким образом, если  по какой-либо причине уменьшается (например, если встречается область с узким «оврагом» или «хребтом»), то поиск должен продолжаться с уменьшенной величиной шага. по какой-либо причине уменьшается (например, если встречается область с узким «оврагом» или «хребтом»), то поиск должен продолжаться с уменьшенной величиной шага. |
