Нелинейное программирование
 Скачать 220.65 Kb. Скачать 220.65 Kb.
|
4.1.2. Метод поиска Хука-Дживса.Метод, разработанный Хуком и Дживсом, является одним из первых алгоритмов, в которых при определении нового направления поиска учитывается информация, полученная на предыдущих итерациях. По существу процедура Хука—Дживса представляет собой комбинацию «исследующего» поиска с циклическим изменением переменных и ускоряющегося поиска по образцу с использованием определенных эвристических правил. Исследующий поиск ориентирован на выявление характера локального поведения целевой функции и определение направлений вдоль «оврагов». Полученная в результате исследующего поиска информация затем используется в процессе поиска по образцу при движении по «оврагам». Исследующий поиск. Для проведения исследующего поиска необходимо задать величину шага, которая может быть различной для разных координатных направлений и изменяться в процессе поиска. Исследующий поиск начинается в некоторой исходной точке. Если значение целевой функции в пробной точке не превышает значения функции в исходной точке, то шаг поиска рассматривается как успешный. В противном случае необходимо вернуться в предыдущую точку и сделать шаг в противоположном направлении с последующей проверкой значения целевой функции. После перебора всех N координат исследующий поиск завершается. Полученную в результате точку называют базовой точкой. Поиск по образцу. Поиск по образцу заключается в реализации единственного шага из полученной базовой точки вдоль-прямой, соединяющей эту точку с предыдущей базовой точкой. Новая точка образца определяется в соответствии с формулой 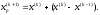 Как только движение по образцу не приводит к уменьшению целевой функция, точка 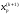 фиксируется в качестве временной базовой точки и вновь проводится исследующий поиск. Если в результате получается точка с меньшим значением целевой функции, чем в точке фиксируется в качестве временной базовой точки и вновь проводится исследующий поиск. Если в результате получается точка с меньшим значением целевой функции, чем в точке 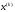 , то она рассматривается как новая базовая точка , то она рассматривается как новая базовая точка 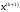 . С другой стороны, если исследующий поиск неудачен, необходимо вернуться в точку . С другой стороны, если исследующий поиск неудачен, необходимо вернуться в точку 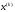 и провести исследующий поиск с целью выявления нового направления минимизации. В конечном счете, возникает ситуация, когда такой поиск не приводит к успеху. В этом случае требуется уменьшить величину шага путем введения некоторого множителя и возобновить исследующий поиск. Поиск завершается, когда величина шага становится достаточно малой. Последовательность точек, получаемую в процессе реализации метода, можно записать в следующем виде: и провести исследующий поиск с целью выявления нового направления минимизации. В конечном счете, возникает ситуация, когда такой поиск не приводит к успеху. В этом случае требуется уменьшить величину шага путем введения некоторого множителя и возобновить исследующий поиск. Поиск завершается, когда величина шага становится достаточно малой. Последовательность точек, получаемую в процессе реализации метода, можно записать в следующем виде: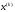 - текущая базовая точка, - текущая базовая точка, 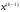 - предыдущая базовая точка, - предыдущая базовая точка,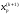 - точка, построенная при движении по образцу, - точка, построенная при движении по образцу,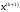 - следующая (новая) базовая точка. - следующая (новая) базовая точка.Приведенная последовательность характеризует логическую структуру поиска по методу Хука — Дживса. Структура метода поиска Хука — Дживса Шаг 1 . Определить: начальную точку 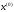 , , приращения 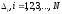 коэффициент уменьшения шага 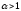 , , параметр окончания поиска 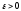 . . Ш а г 2. ровести исследующий поиск. Ш а г 3. Был ли исследующий поиск удачным (найдена ли точка с меньшим значением целевой функции)? Да: перейти к шагу 5. Нет: продолжать. Ш а г 4. Проверка на окончание поиска. Выполняется ли неравенство 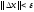 ? ?Да: прекратить поиск; текущая точка аппроксимирует точку оптимума  . .Нет: уменьшить приращения по формуле 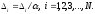 Перейти к шагу 2. Ш а г 5. Провести поиск по образцу: 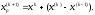 Шаг 6. Провести исследующий поиск, используя 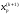 в качестве базовой точки; в качестве базовой точки;пусть 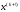 полученная в результате точка. полученная в результате точка.Ш а г 7. Выполняется ли неравенство 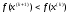 ? ? Да: положить 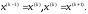 Перейти к шагу 5. Перейти к шагу 5. Нет: перейти к шагу 4. Пример 6 Поиск по методу Хука — Дживса Найти точку минимума функции 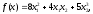 используя начальную точку используя начальную точку 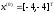 . .Решение. Для того чтобы применить метод прямого поиска .Хука — Дживса, необходимо задать следующие величины: 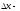 векторная величина приращения = векторная величина приращения = 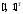 , ,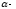 коэффициент уменьшения шага = 2, коэффициент уменьшения шага = 2, 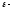 параметр окончания поиска = 10-4. параметр окончания поиска = 10-4.Итерации начинаются с исследующего поиска вокруг точки 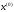 , которой соответствует значение функции , которой соответствует значение функции 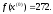 Фиксируя Фиксируя 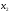 , дадим приращение переменной , дадим приращение переменной 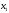 : :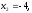 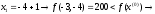 Успех. Успех.Следовательно, необходимо зафиксировать 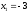 и дать приращение переменной и дать приращение переменной 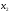 : :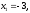 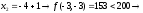 Успех. Успех.Таким образом, в результате исследующего поиска найдена точка 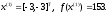 Поскольку исследующий поиск был удачным, переходим к поиску по образцу: 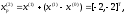 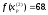 Далее проводится исследующий поиск вокруг точки 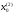 , который оказывается удачным при использовании положительных приращений переменных х1 и х2. В результате получаем точку , который оказывается удачным при использовании положительных приращений переменных х1 и х2. В результате получаем точку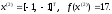 Поскольку 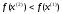 , поиск по образцу следует считать успешным, и , поиск по образцу следует считать успешным, и 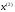 становится новой базовой точкой при следующем проведении поиска по образцу. Итерации продолжаются, пока уменьшение величины шага не укажет на окончание поиска в окрестности точки минимума. Последовательные шаги реализации метода показаны на рисунке. становится новой базовой точкой при следующем проведении поиска по образцу. Итерации продолжаются, пока уменьшение величины шага не укажет на окончание поиска в окрестности точки минимума. Последовательные шаги реализации метода показаны на рисунке.Из примера следует, что метод Хука — Дживса характеризуется несложной стратегией поиска, относительной простотой вычислений и невысоким уровнем требований к объему памяти ЭВМ, который оказывается даже ниже, чем в случае использования метода поиска по симплексу. 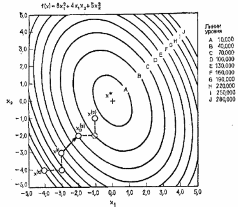 Итерации поиска по методу Хука-Дживса на примере |
