Нелинейное программирование
 Скачать 220.65 Kb. Скачать 220.65 Kb.
|
2.2. Множители ЛагранжаС помощью метода множителей Лагранжа по существу устанавливаются необходимые условия, позволяющие идентифицировать точки оптимума в задачах оптимизации с ограничениями в виде равенств. При этом задача с ограничениями преобразуется в эквивалентную задачу безусловной оптимизации, в которой фигурируют некоторые неизвестные параметры, называемые множителями Лагранжа. Рассмотрим задачу минимизации функции n переменных с учетом одного ограничения в виде равенства: Минимизировать  (3) (3)при ограничениях 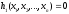 (4) (4)В соответствии с методом множителей Лагранжа эта задача преобразуется в следующую задачу безусловной оптимизации: минимизировать L(x,u)=f(x)-u*h(x) (5) Функция L(х;u) называется функцией Лагранжа, u — неизвестная постоянная, которая носит название множителя Лагранжа. На знак u никаких требований не накладывается. Пусть при заданном значении u=u0 безусловный минимум функции L(x,u) по х достигается в точке 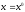 и и 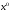 удовлетворяет уравнению удовлетворяет уравнению 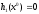 . Тогда, как нетрудно видеть, x0 минимизирует (1) с учетом (4), поскольку для всех значений х, удовлетворяющих (4), . Тогда, как нетрудно видеть, x0 минимизирует (1) с учетом (4), поскольку для всех значений х, удовлетворяющих (4),  и L(x,u)=min f(x). и L(x,u)=min f(x). Разумеется, необходимо подобрать значение u=u° таким образом, чтобы координата точки безусловного минимума х° удовлетворяла равенству (4). Это можно сделать, если, рассматривая u как переменную, найти безусловный минимум функции (5) в виде функции u, а затем выбрать значение u, при котором выполняется равенство (4). Проиллюстрируем это на конкретном примере. Пример 2 Минимизировать 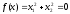 при ограничении 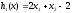 =0 =0Соответствующая задача безусловной оптимизации записывается в следующем виде: минимизировать L(x,u)= 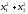 -u -u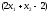 Решение. Приравняв две компоненты градиента L к нулю, получим 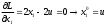 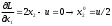 Для того чтобы проверить, соответствует ли стационарная точка х° минимуму, вычислим элементы матрицы Гессе функции L(х;u), рассматриваемой как функция х, 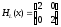 , ,которая оказывается положительно определенной. Это означает, что L(х,,u) — выпуклая функция х. Следовательно, координаты 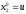 , ,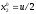 определяют точку глобального минимума. Оптимальное значение u находится путем подстановки значений определяют точку глобального минимума. Оптимальное значение u находится путем подстановки значений 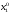 и и 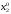 в уравнение в уравнение 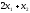 =2, откуда 2u+u/2=2 или =2, откуда 2u+u/2=2 или 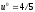 . Таким образом, условный минимум достигается при . Таким образом, условный минимум достигается при 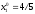 и и  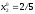 и равен min f(x)=4/5. и равен min f(x)=4/5.При решении задачи из примера 2 мы рассматривали L(х;u) как функцию двух переменных 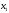 и и 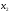 и, кроме того, предполагали, что значение параметра u выбрано так, чтобы выполнялось ограничение. Если же решение системы и, кроме того, предполагали, что значение параметра u выбрано так, чтобы выполнялось ограничение. Если же решение системы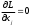 , j=1,2,3,…,n , j=1,2,3,…,nв виде явных функций u получить нельзя, то значения х и u находятся путем решения следующей системы, состоящей из n+1 уравнений с n+1 неизвестными: 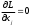 , j=1,2,3,…,n , j=1,2,3,…,n  Для нахождения всех возможных решений данной системы можно использовать численные методы поиска (например, метод Ньютона). Для каждого из решений ( 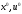 ) следует вычислить элементы матрицы Гессе функции L, рассматриваемой как функция х, и выяснить, является ли эта матрица положительно определенной (локальный минимум) или отрицательно определенной (локальный максимум). ) следует вычислить элементы матрицы Гессе функции L, рассматриваемой как функция х, и выяснить, является ли эта матрица положительно определенной (локальный минимум) или отрицательно определенной (локальный максимум).Метод множителей Лагранжа можно распространить на случай, когда задача имеет несколько ограничений в виде равенств. Рассмотрим общую задачу, в которой требуется Минимизировать f(x) при ограничениях 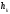 =0, k=1, 2, ..., К. =0, k=1, 2, ..., К.Функция Лагранжа принимает следующий вид: L(x,u)=f(x)- 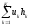 Здесь 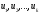 —множители Лагранжа, т.е. неизвестные параметры, значения которых необходимо определить. Приравнивая частные производные L по х к нулю, получаем следующую систему n уравнении с n неизвестными: —множители Лагранжа, т.е. неизвестные параметры, значения которых необходимо определить. Приравнивая частные производные L по х к нулю, получаем следующую систему n уравнении с n неизвестными: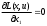 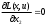 ……….. 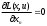 Если найти решение приведенной выше системы в виде функций вектора u оказывается затруднительным, то можно расширить систему путем включения в нее ограничений в виде равенств  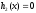 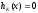 Решение расширенной системы, состоящей из n+К уравнений с n+К неизвестными, определяет стационарную точку функции L. Затем реализуется процедура проверки на минимум или максимум, которая проводится на основе вычисления элементов матрицы Гессе функции L, рассматриваемой как функция х, подобно тому, как это было проделано в случае задачи с одним ограничением. Для некоторых задач расширенная система n+К уравнений с n+K неизвестными может не иметь решений, и метод множителей Лагранжа оказывается неприменимым. Следует, однако, отметить, что такие задачи на практике встречаются достаточно редко. |
