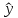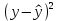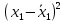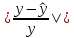РГР_МАД. Необходимо Вычислить выборочное среднее по первым 25 значениям, вычислить выборочное среднее по всему объему выборки. Сравнить
 Скачать 163.37 Kb. Скачать 163.37 Kb.
|
|
Задание 2. По 20 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от ввода в действие новых основных фондов x1 (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих x2 (%) (смотри таблицу 6). Таблица 6
Требуется: А. Изучение основ корреляционного анализа – построить поля корреляции; – получить корреляционную матрицу; – проанализировать корреляционную матрицу и сделать вывод о возможности построения регрессии (указать конкретный вид модели). Б. Изучение основ регрессионного анализа. Построение модели парной линейной регрессии – получить линейное уравнение парной регрессии, выбрав в качестве зависимой переменной – Y, в качестве независимой переменной Xi, наиболее сильно связанную с Y; – определить коэффициент парной линейной корреляции и коэффициент детерминации полученной модели; – проверить значимость построенной модели по статистике Фишера, используя уровень значимости α = 0,05; – если модель значима, дать оценку коэффициентов парной линейной регрессии на основе t-критерия Стьюдента; – проверить адекватность полученной регрессионной модели. В. Изучение основ регрессионного анализа. Построение модели множественной линейной регрессии - получить линейное уравнение множественной регрессии, выбрав в качестве зависимой переменной – Y, в качестве независимых переменных Xi,соответствующие варианту и наиболее сильно связанных с Y; – определить коэффициент множественной корреляции и коэффици-ент детерминации полученной модели; – проверить значимость построенной модели по статистике Фишера, используя уровень значимости α = 0,05; – если модель значима, дать оценку коэффициентов множественной регрессии на основе t-критерия Стьюдента; – пересчитать уравнение множественной регрессии, используя толь-ко значимые факторы; – проверить адекватность полученной регрессионной модели. Решение. А. Изучение основ корреляционного анализа – построим поля корреляции (рис. 2 и 3) 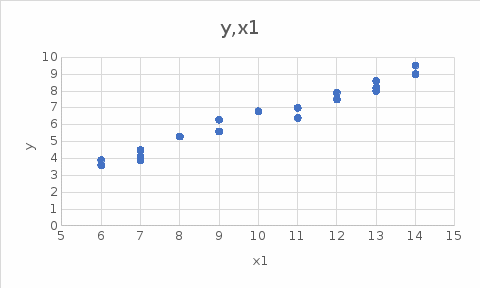 Рис.2 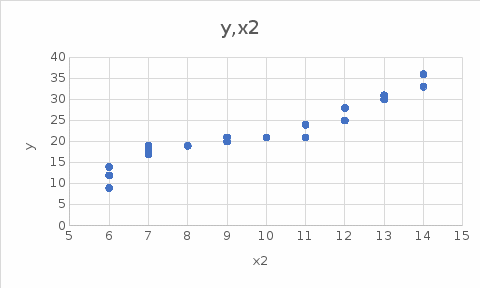 Рис.3 – получим корреляционную матрицу (рис. 4) 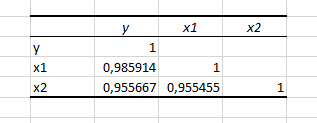 Рис.4 Корреляционная матрицы показывает, что между y и x1, а также y и x2 существует сильная линейная связь. Значит возможно построить линейную регрессионную модель вида: 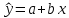 Б. Изучение основ регрессионного анализа. Построение модели парной линейной регрессии – получим линейное уравнение парной регрессии, выбрав в качестве зависимой переменной – Y, в качестве независимой переменной Xi, наиболее сильно связанную с Y; Наиболее сильно связана с y переменная x1. Составим расчетную таблицу 7. Таблица 7
Для нахождения коэффициентов составим систему уравнений: 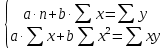 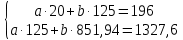 Решив систему, получим: 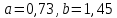 Модель имеет вид: 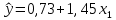 При увеличении ввода в действие основных фондов на 1% (от стоимости фондов на конец года) выработка продукции на одного работника увеличится в среднем на 1,45 тыс.руб. – определим коэффициент парной линейной корреляции и коэффициент детерминации полученной модели Коэффициент парной линейной корреляции: 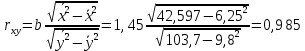 Линейная связь междувыработкой продукции на одного работника y(тыс. руб.) и вводом в действие новых основных фондов 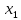 (% от стоимости фондов на конец года) сильная. (% от стоимости фондов на конец года) сильная.Коэффициент детерминации: 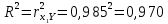 Полученная линейная модель на 97% объясняет изменение 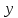 (выработка продукции на одного работника, тыс.руб. изменением (выработка продукции на одного работника, тыс.руб. изменением 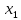 (ввод в действие новых основных фондов в % от стоимости фондов на конец года). Остальные 3% изменений y объясняются неучтенными в модели признаками. (ввод в действие новых основных фондов в % от стоимости фондов на конец года). Остальные 3% изменений y объясняются неучтенными в модели признаками.– проверим значимость построенной модели по статистике Фишера, используя уровень значимости α = 0,05 F- статистика Фишера: 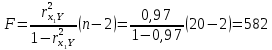 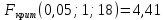 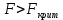 - построенная линейная модель регрессии статистически значима. - построенная линейная модель регрессии статистически значима.– дадим оценку коэффициентам парной линейной регрессии на основе t-критерия Стьюдента Составим расчетную таблицу 8. Таблица 8
Стандартные ошибки параметров регрессии: 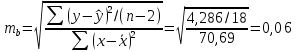 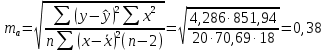 t-статистики: 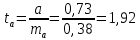 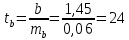 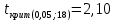 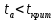 – коэффициент – коэффициент 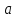 статистически не значим на уровне значимости 0,05; статистически не значим на уровне значимости 0,05;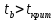 – коэффициент – коэффициент 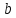 статистически значим на уровне значимости 0,05. статистически значим на уровне значимости 0,05.– проверим адекватность полученной регрессионной модели. Полученное расчетное значение F-критерия Фишера значительно превосходит критическое, коэффициент регрессии 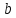 статистически значим. статистически значим. Определим среднюю ошибку аппроксимации: 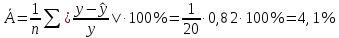 Полученное значение средней ошибки аппроксимации свидетельствует о хорошем подборе модели к исходным данным. Таким образом, построенная модель в целом можно считать адекватной. |