РГР_МАД. Необходимо Вычислить выборочное среднее по первым 25 значениям, вычислить выборочное среднее по всему объему выборки. Сравнить
 Скачать 163.37 Kb. Скачать 163.37 Kb.
|
|
В. Изучение основ регрессионного анализа. Построение модели множественной линейной регрессии - получим линейное уравнение множественной регрессии, выбрав в качестве зависимой переменной – Y, в качестве независимых переменных Xi Построим модель множественной линейной регрессии вида 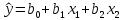 с помощью инструмента Анализ данных - Регрессия в Excel (рис.5) с помощью инструмента Анализ данных - Регрессия в Excel (рис.5)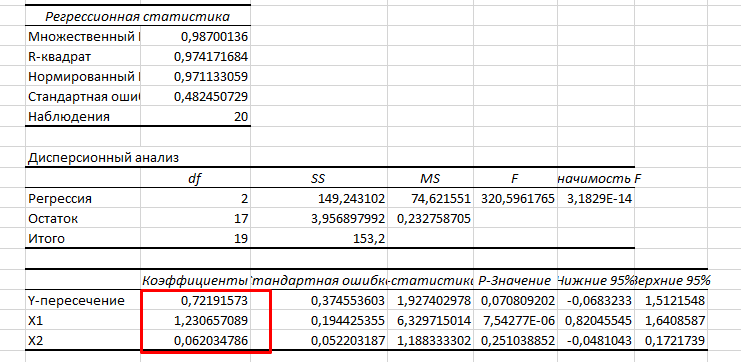 Рис. 5 Модель множественной линейной регрессии имеет вид: 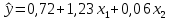 – определим коэффициент множественной корреляции и коэффициент детерминации полученной модели (рис.6). 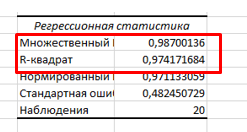 Рис. 6 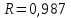 , , 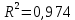 Коэффициент множественной корреляции характеризует совокупное влияние всех независимых переменных на зависимую переменную в модели множественной регрессии. В нашем случае, совокупная взаимосвязь между выработкой продукции на одного работника y (тыс. руб.) и вводом в действие новых основных фондов x1 (% от стоимости фондов на конец года) и удельным весом рабочих высокой квалификации в общей численности рабочих x2 (%) сильная. Коэффициент детерминации показывает какая доля дисперсии зависимой переменной объясняется влиянием независимых переменных. В нашем случае 97,4% дисперсии выработки продукции на одного работника y (тыс. руб.) объясняется влиянием признаков x1 (вводом в действие новых основных фондов в % от стоимости фондов на конец года) и x2 (удельный вес рабочих высокой квалификации в общей численности рабочих в %), а 2,6 % неучтенными в модели признаками. – проверим значимость построенной модели по статистике Фишера, используя уровень значимости α = 0,05 F-статистика (рис.7):  Рис.7 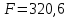 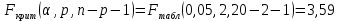 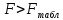 Уравнение регрессии статистически значимо на уровне значимости 0,05 – дадим оценку коэффициентам множественной регрессии на основе t-критерия Стьюдента t – статистики (рис.8)  Рис.8 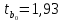 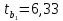 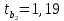 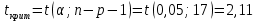 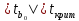 – коэффициент – коэффициент 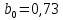 статистически не значим на уровне значимости 0,05 статистически не значим на уровне значимости 0,05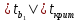 – коэффициент – коэффициент 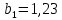 статистически значим на уровне значимости 0,05 статистически значим на уровне значимости 0,05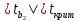 – коэффициент – коэффициент 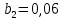 статистически не значим на уровне значимости 0,05 статистически не значим на уровне значимости 0,05– пересчитаем уравнение множественной регрессии, используя только значимый фактор с помощью инструмента Анализ данных-Регрессия в Excel (рис.9) 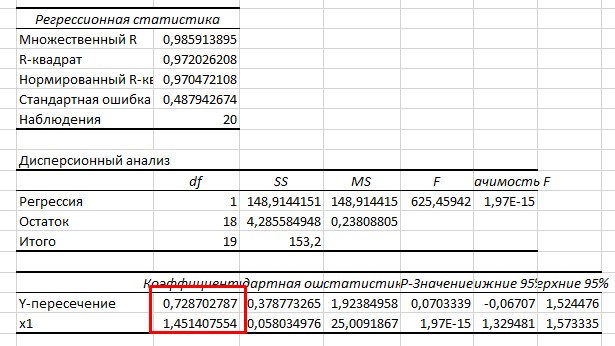 Рис. 9 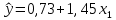 В пункте Б установлено, что построенную модель в целом можно считать адекватной. |
