Метод. Метод рационализации. Неравенства, решаемые методом рационализации httpsshkolkovo netcatalogreshenie neravenstv metodom racionalizacii
 Скачать 2.42 Mb. Скачать 2.42 Mb.
|
|
Неравенства, решаемые методом рационализации https://shkolkovo.net/catalog/reshenie_neravenstv/_metodom_racionalizacii © shkolkovo.net  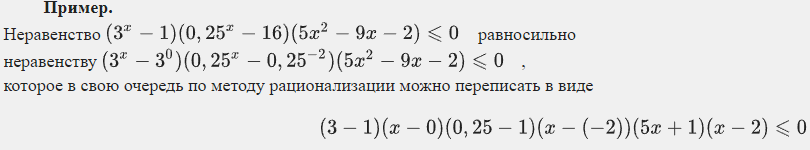     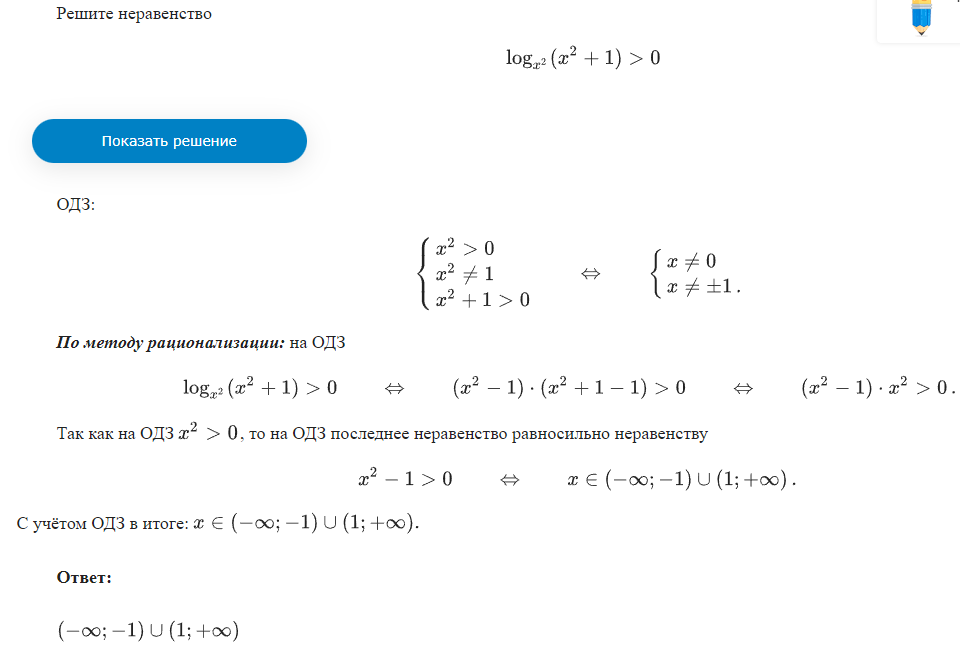   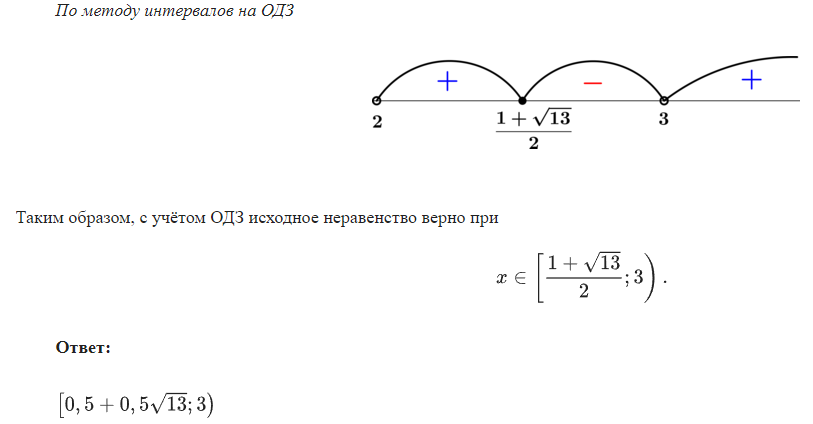    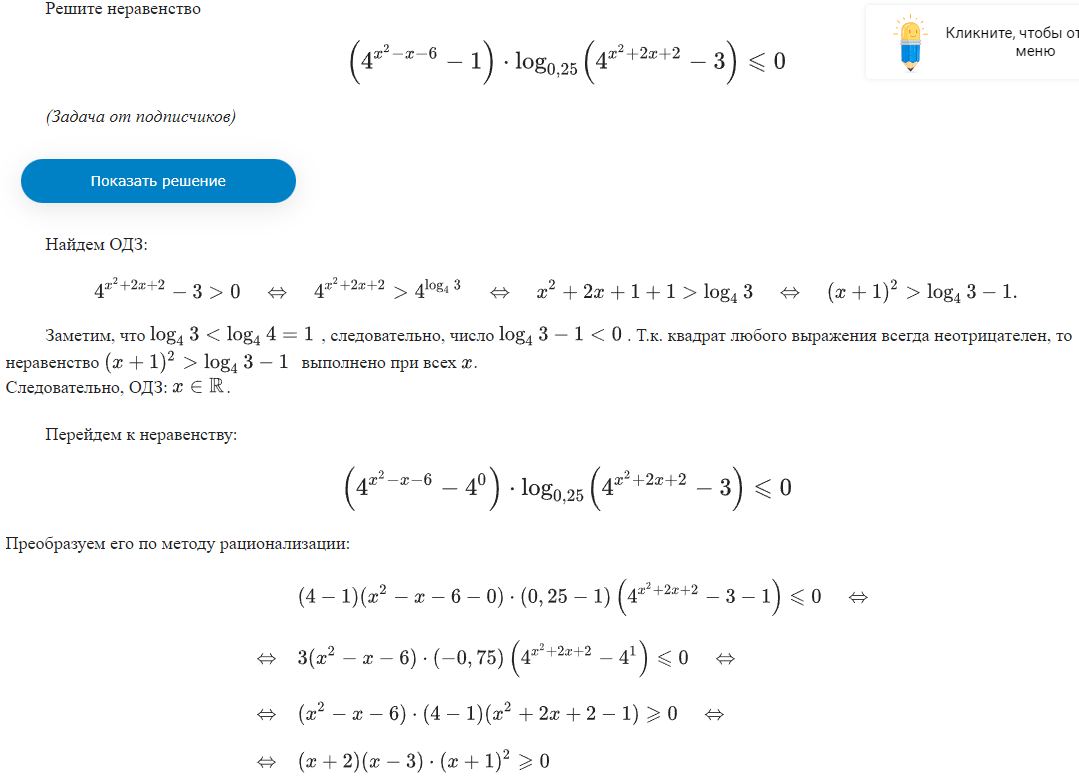  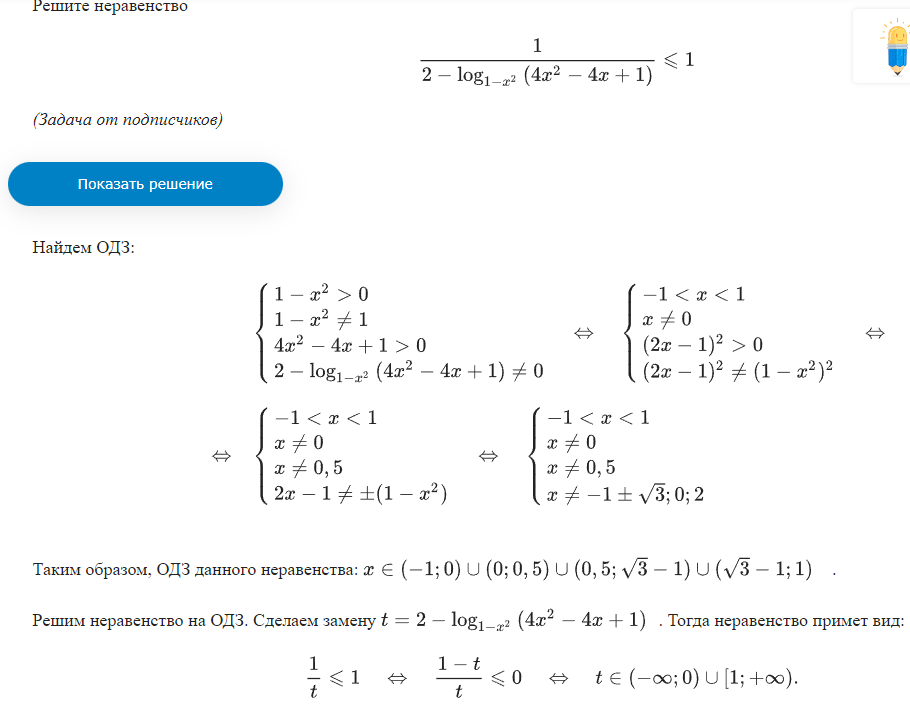  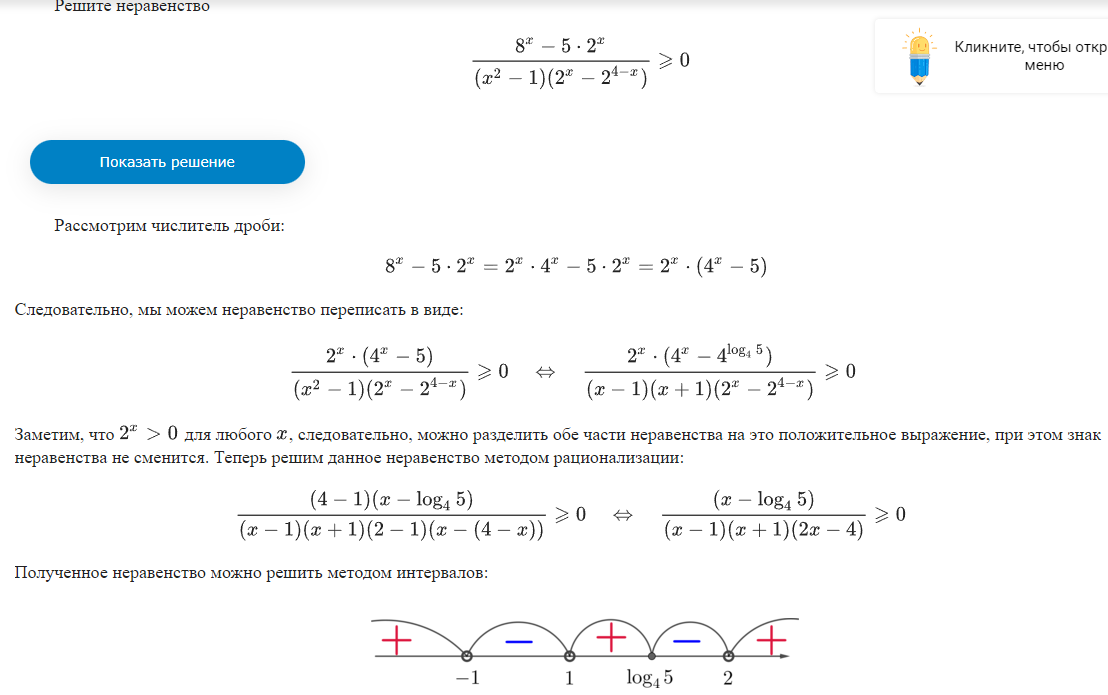 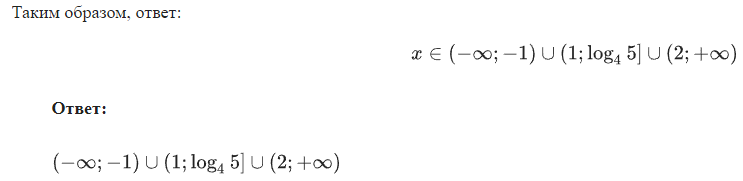     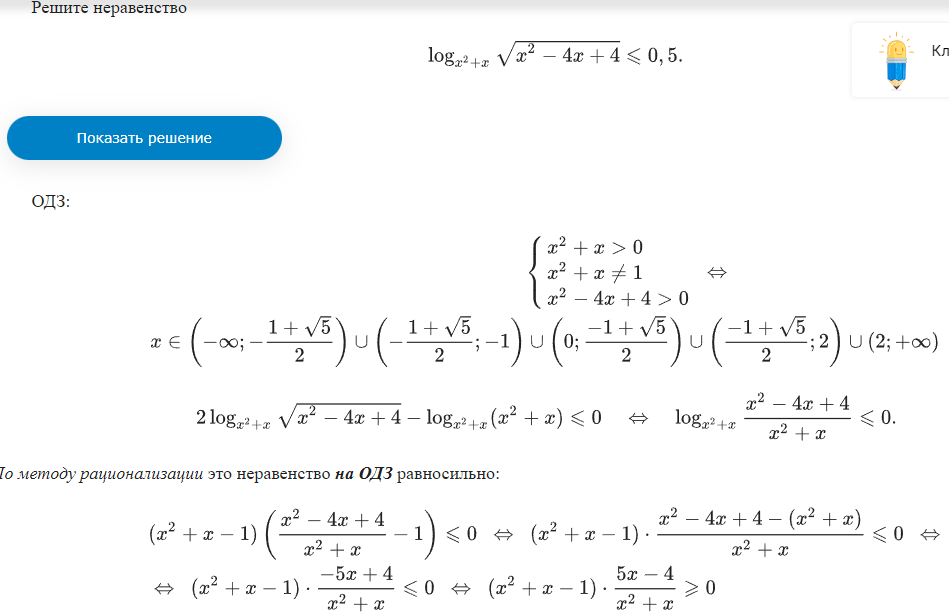   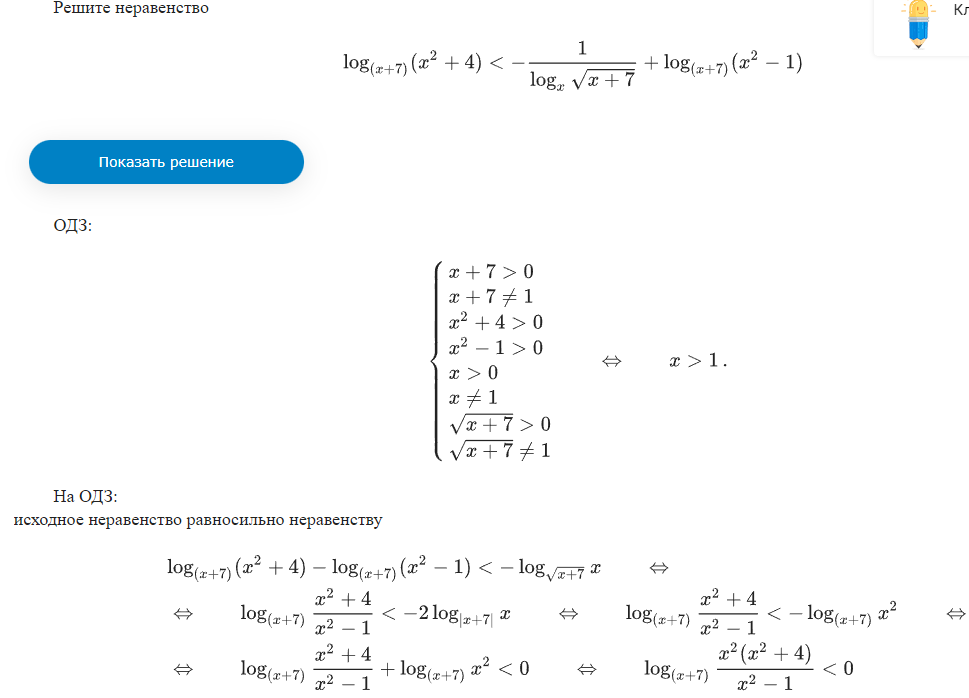  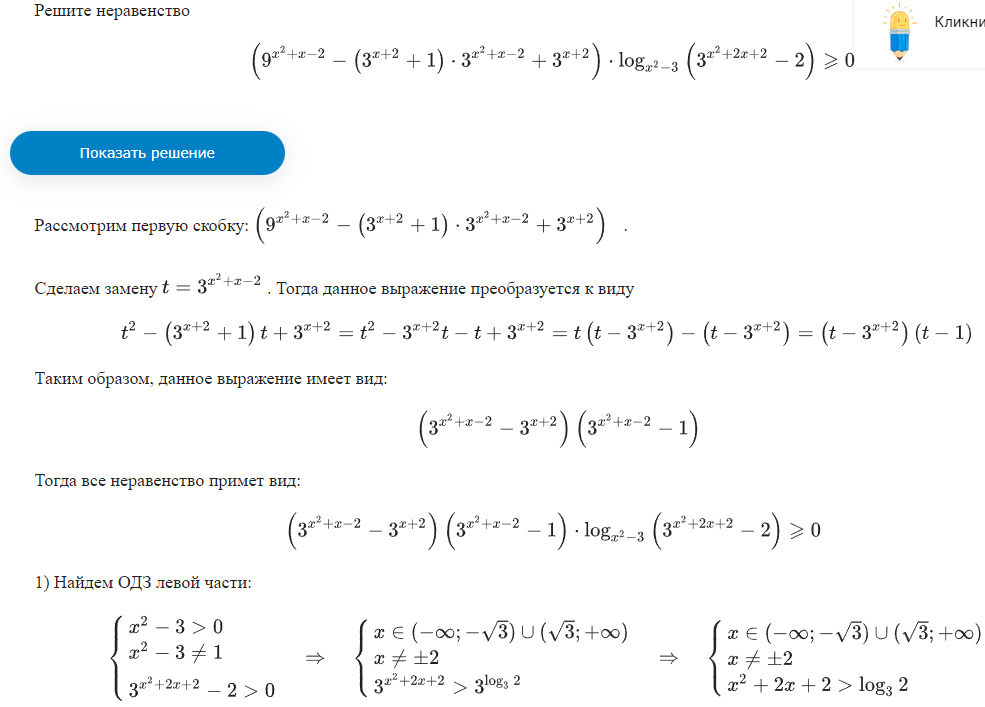  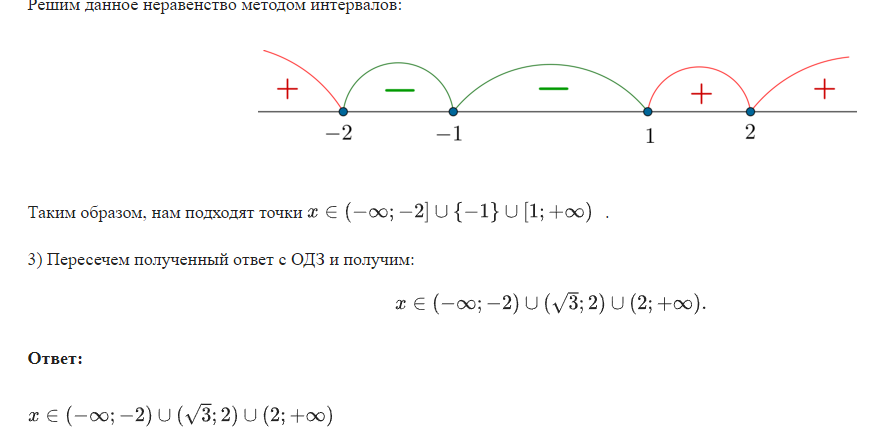  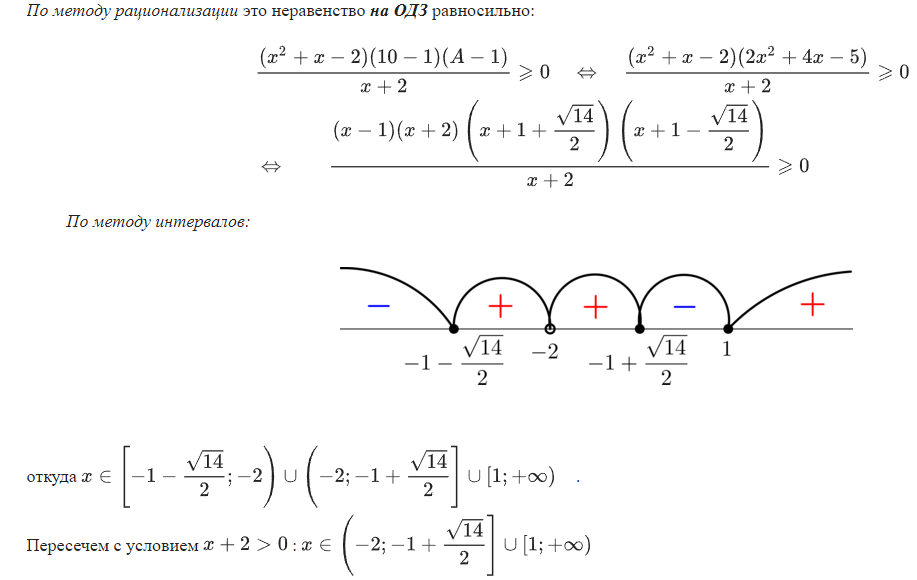 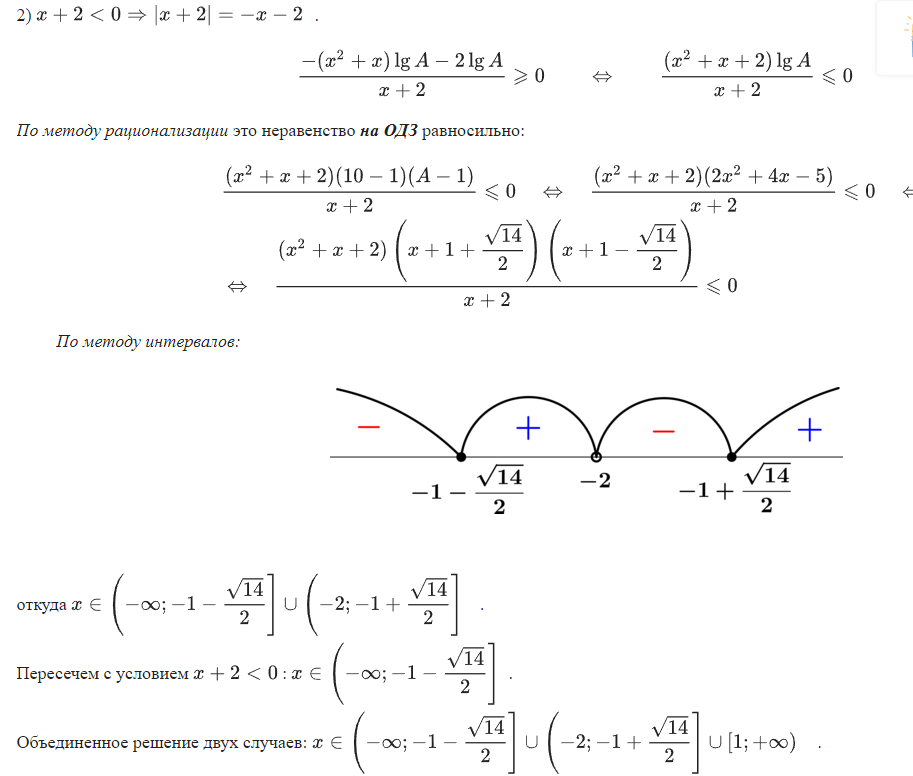 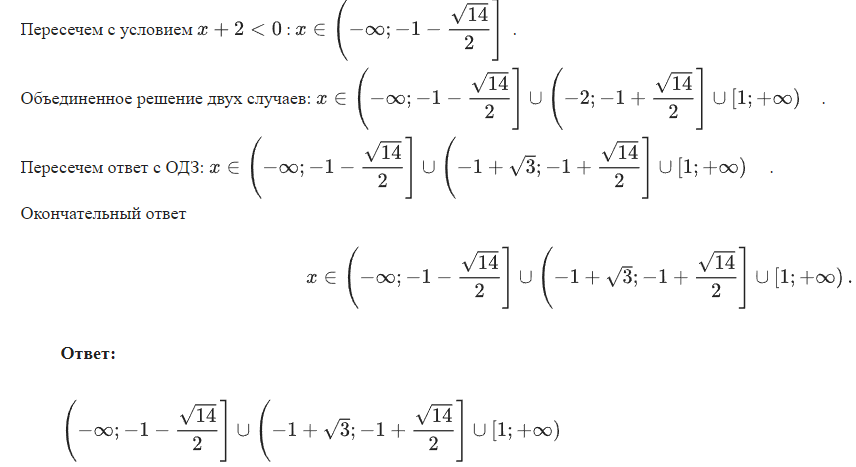         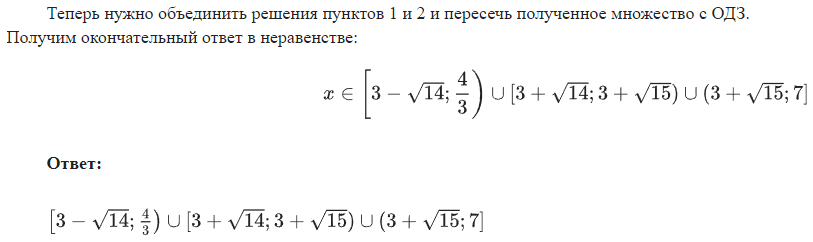 Разные названия одного метода В различных пособиях этот метод называют по-разному: метод рационализации метод замены множителей метод знакотождественных множителей Я не смог обнаружить существенных различий между всеми этими методами, поэтому предлагаю считать всё вышеперечисленное разными названиями одного и того же метода. Далее я буду использовать название "метод рационализации". Основная идея Основная идея метода рационализации в том, чтобы перейти от решения исходного "сложного" неравенства (логарифмического, показательного или смешанного) к решению более простого (как правило, дробно-рационального) неравенства, которое можно решить методом интервалов. Например, 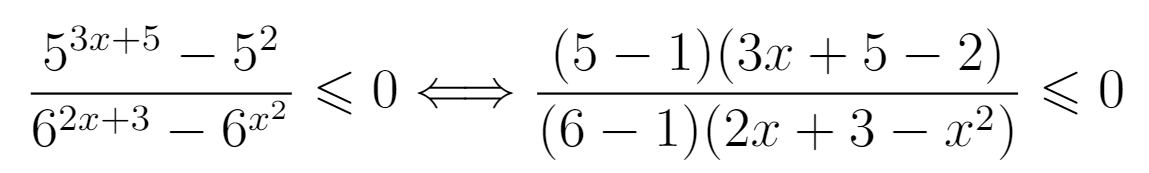 Равносильный переход от показательного неравенства Обратите внимание, что переход является равносильным. Это означает, что множество корней левого неравенства совпадает с множеством корней правого неравенства. То есть мы заменили решение "сложного" неравенства (в котором переменная находится в показателе степени) решением более простого дробно-рационального неравенства. В некоторых случаях необходимо выполнить переход от "сложного" неравенства к системе более простых неравенств. Например, 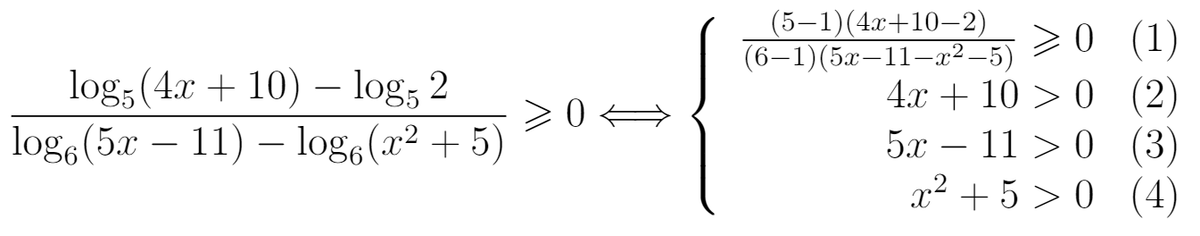 Равносильный переход от логарифмического неравенства Идея данного перехода такая же, как и в предыдущем примере, - перейти от "сложного" неравенства (в котором переменная находится под знаком логарифма) к системе из более простых неравенств, которые можно решить методом интервалов (разумеется, после некоторых преобразований). Замечу, что неравенство (4), записанное в системе, является избыточным: оно верно при любых действительных значениях x. Поэтому неравенство (4) можно исключить из системы (при этом множество решений системы не изменится). Кроме этого, система, составленная из неравенств (2), (3) и (4) не описывает ОДЗ исходного (левого) неравенства. Например, число 4 удовлетворяет неравенствам (2), (3), (4), но не входит в ОДЗ исходного неравенства. Поэтому нельзя в бланке ответов писать рядом с условиями (2), (3) и (4) слово ОДЗ, потому что это не ОДЗ! Неравенства (2), (3), (4) - это условия, которые должны быть записаны в системе, чтобы переход был равносильным. В 2018 и 2019 годах многие участники экзамена получали 0 баллов в задании 15 именно из-за того, что писали слово ОДЗ рядом с условиями, которые не описывали ОДЗ. Слово ОДЗ следует писать только рядом с теми условиями, которые действительно описывают ОДЗ исходного неравенства. Теоремы метода рационализации Метод рационализации базируется на 4 теоремах, каждая из которых утверждает, что такой-то переход является равносильным. Я собрал все эти 4 теоремы на одной картинке: 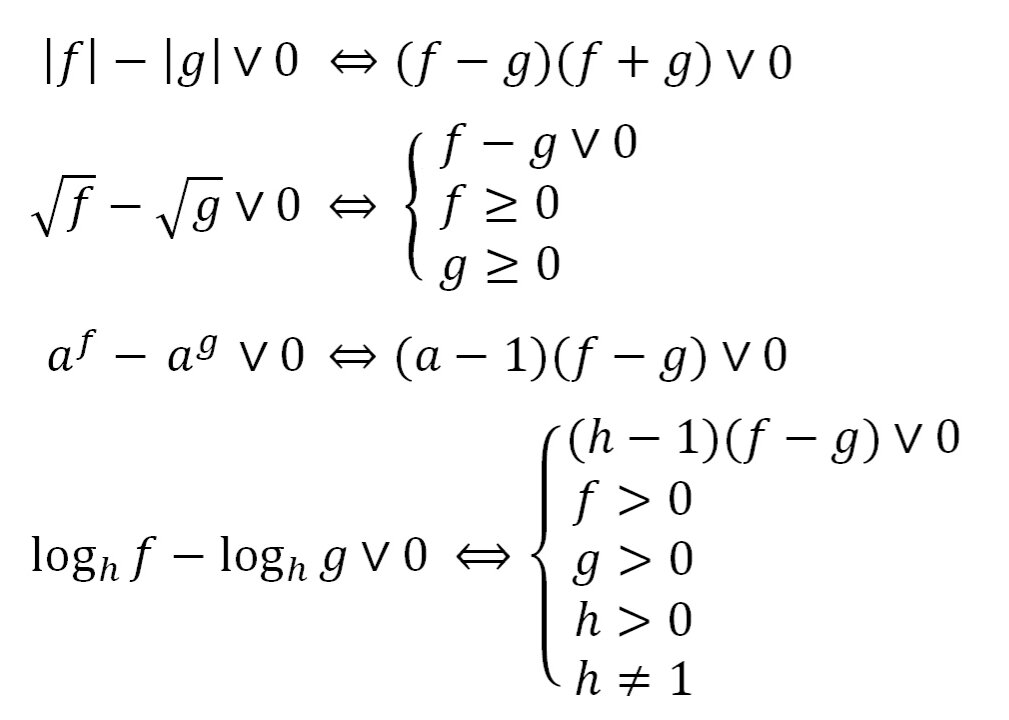 Четыре теоремы о равносильных переходах в методе рационализации Вместо знака "галочка" можно использовать любой из пяти знаков: больше, меньше, больше или равно, меньше или равно, равно. Буквой a обозначено положительное действительное число, не зависящее от х. Буквами f, g, h обозначены выражения, которые могут содержать переменную x (а могут и не содержать). Отмечу, что равносильный переход в иррациональных неравенствах (вторая теорема) вряд ли пригодится на ЕГЭ при решении задания 15. По словам Иван Валериевича Ященко (руководителя Федеральной комиссии разработчиков КИМ ЕГЭ и ОГЭ по математике) в задании 15 профильного ЕГЭ по математике нет иррациональных неравенств. Но я решил не исключать этот переход из списка, потому что иррациональные уравнения могут встретиться на различных олимпиадах ("РосАтом", "ФизТех", "ОММО"), а также в ЕГЭ в задании 18. Основываясь на этих теоремах можно решать широкий круг неравенств. Для этого необходимо сделать так, чтобы в правой части неравенства стоял 0, а в левой части неравенства - произведение или частное скобок. Если в какой-то из скобок стоит разность модулей, арифметических квадратных корней, степеней или логарифмов с одинаковым основанием, то можно совершить равносильный переход, заменив эту скобку более простым выражением и (при необходимости), дописав в систему необходимые условия (пример будет ниже, в следующем разделе). Как оформлять метод рационализации на ЕГЭ? В 2020 году я писал профильный ЕГЭ по математике и набрал 96 баллов из 100. Задание 15 в моей работе было оценено максимальным баллом. Я использовал в решении метод равносильных переходов и рядом с одним из равносильных переходов написал фразу "метод рационализации": 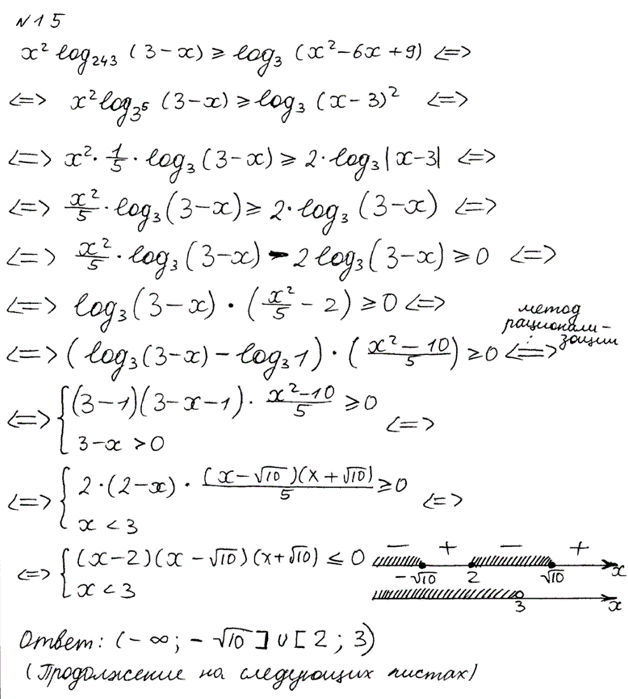 Метод рационализации Метод рационализации — это процедура, позволяющая в определённых случаях упростить неравенство и свести его к рациональному неравенству (которое решается методом интервалов). Позволяет перейти от выражения f к выражению g, сохранив все решения. Метод рационализации для логарифмических неравенств Здесь мы сравниваем значения относительно друг друга и допускаем случай, когда одно значение больше, а другое меньше и наоборот. Один из способов сравнения двух величин – это вычесть из одного другое. Если разность будет больше нуля, значит, первое число было больше. В первой скобке мы вычитаем из основания единицу. Это значит, что мы сравниваем основание с 1. Во второй скобке мы из одного под логарифмического выражения вычитаем другое, т.е. снова сравниваем их. Пример. Решите неравенство Решение. ОДЗ: 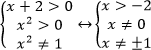 Преобразуем неравенство Воспользуемся методом рационализации: Нам нужно найти такие х, при которых левое выражение меньше правого. В записанном неравенстве, если основание больше единицы, первая скобка будет положительна, и если первое подлогарифмическое выражение будет меньше второго, то их разность будет меньше 0, т.е. вторая скобка будет меньше нуля и это как раз те решения, что нужны нам по условию. Если же основание будет меньше единицы, первая скобка будет отрицательна, что изменит общий знак неравенства. Так же мы действовали, когда писали равносильный переход в виде двух случаев для логарифмического неравенства. 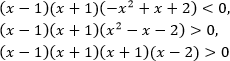 С учетом ОДЗ получаем решение неравенства: Ответ: Из рассмотренного метода рационализации вытекают следствия:  Пример. Решите неравенство: Решение. ОДЗ: 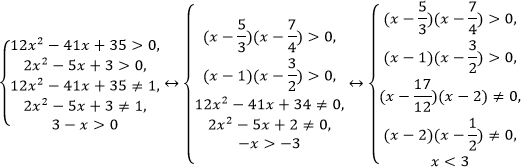 Применим метод рационализации: 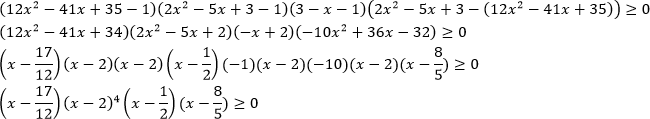 С учетом ОДЗ: Ответ: Метод рационализации для неравенств с модулем  При сравнении двух чисел по модулю нас не интересует знак числа, поэтому можем от знака избавиться при помощи чётной степени. избавит нас от знака. При дальнейшей работе с полученным неравенством выполнять возведение в квадрат не обязательно, лучше применить формулу разности квадратов. Пример. Решите неравенство Решение. Воспользуемся методом рационализации: 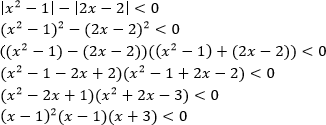 Решением неравенства является интервал (-3;1) Ответ: Пример. Решите неравенство Решение. Воспользуемся равносильным переходом: 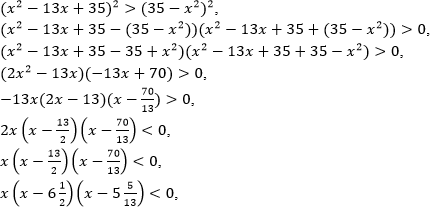 Решением неравенства является промежуток Ответ: Метод рационализации для иррациональных неравенств  Пример. Решите неравенство Решение. ОДЗ (находим ОДЗ для меньшего из выражений, ОДЗ для большего выражения выполнится автоматически): 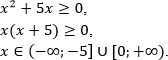 Воспользуемся методом рационализации: 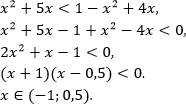 С учетом ОДЗ получаем окончательное решение неравенства: Ответ: Метод рационализации для показательных неравенств  Для показательно-степенных неравенств действуют те же правила, что и для логарифма. При основании, большем 1, знак неравенства мы можем сохранить, при основании меньше единицы, знак неравенства должен измениться при переходе к степеням. Тогда мы можем записать это, как произведение двух скобок, в первой мы будем сравнивать основание с единицей, а во второй – значения показателей степеней. Пример. Решите неравенство ОДЗ: Воспользуемся методом рационализации: 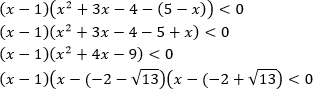 Видим, что решением является промежуток: С учетом ОДЗ: Ответ: Сведем все рассмотренные равносильные преобразования в таблицу  |
