Матрицы. Невырожденная матрица
 Скачать 2.6 Mb.
|
|
Матрицы 1. Сложение. Складывать матрицы можно только одного размера! 2. Умножение. Две матрицы можно перемножить между собой тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы! Невырожденная матрица (иначе неособенная матрица) ― квадратная матрица, определитель которой отличен от нуля. В противном случае матрица называется вырожденной. detA ≠ 0 3. Обратная матрица Обратная матрица существует только для квадратных матриц определитель которых не равен нулю. 4. Ранг Свойства матрицы связанные с рангом Ранг матрицы не изменится, если к ее строкам (столбцам) применить элементарные преобразования. Ранг ступенчатой матрицы равен количеству её ненулевых строк. Данная матрица имеет размер 3×5, т.е. содержит три строки и пять столбцов. Из чисел 3 и 5 минимальным является 3, посему ранг матрицы A не больше 3, т.е. rangA≤3. И это неравенство очевидно, так как миноры четвёртого порядка образовать мы уже не сможем, – для них нужно 4 строки, а у нас всего 3. 5. Элементраные преобразования Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц, то есть, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица. Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду. Элементарными преобразованиями строк называют: перестановку местами любых двух строк матрицы; умножение на ненулевую константу любой строки матрицы; прибавление к любой строке матрицы другой строки, умноженной на ненулевое число. Аналогично определяются элементарные преобразования столбцов. Элементарные преобразования не изменяют ранг матрицы. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. 6. Теорема Капелли Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:
Для того чтобы линейная система являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу её основной матрицы. Доказана Леопо́льдом Кро́некером, Альфре́до Капе́лли. 7. Метод Крамера Вектора. Какая физ величина определяется скалярным произведением? Скорость, сила, объем, масса, РАБОТА. 1. Скалярное произведение векторов Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними. Равные вектора это те вектора у которых длина и направление равны.(х1=х2,у1=у2 и тд). Нулевые вектора, те у которых длина равна 0. Коллинеарные это те, у которых отношение координат равно, т.е. х1/х2=у1/у2=и тд. Е  диничные вектора, у них длинна равна 1.Сверху скалярное произведение векторов. Снизу длина векторов(модули векторов). У ортоганальных векторов, угол между векторами равен 0, следовательно между ними 90 градусов. А  также если скалярное произведение векторов равно 0.ОРТ ВЕКТОРА Если даны координаты. 1. находим длину вектора. 2. делим координаты на длину. Е 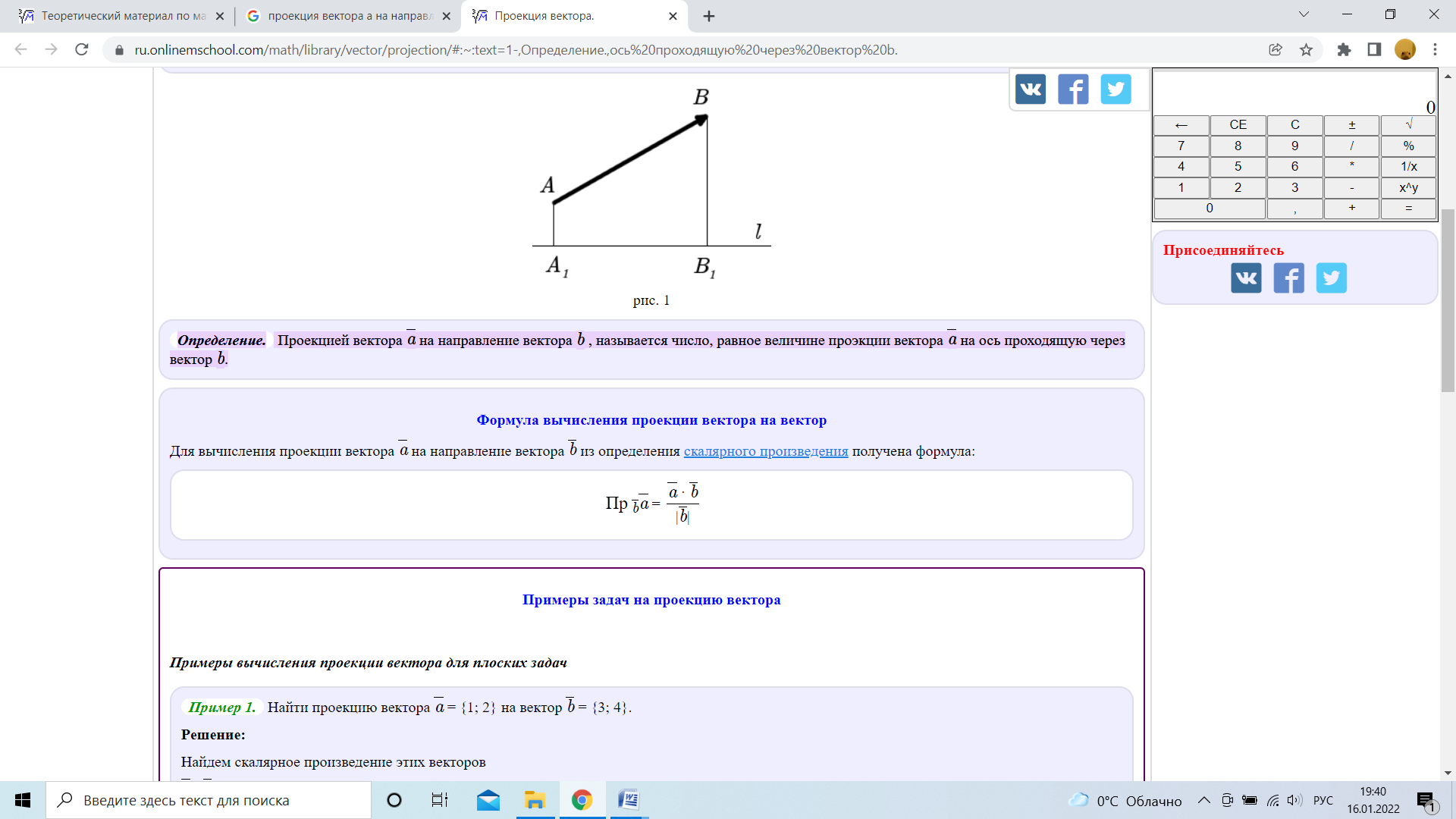 сли длина вектора равна 1, то этот вектор является ортом.  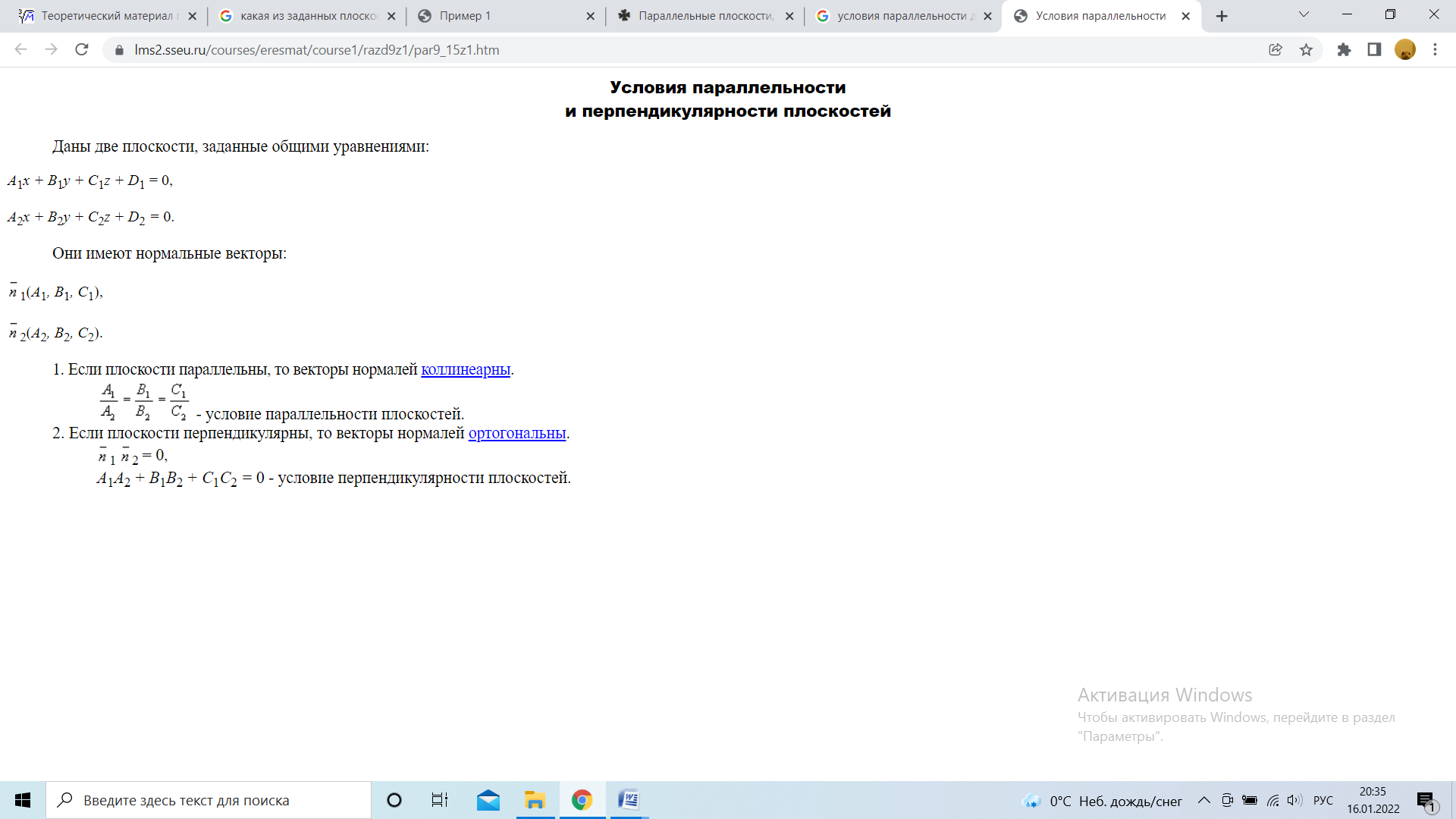  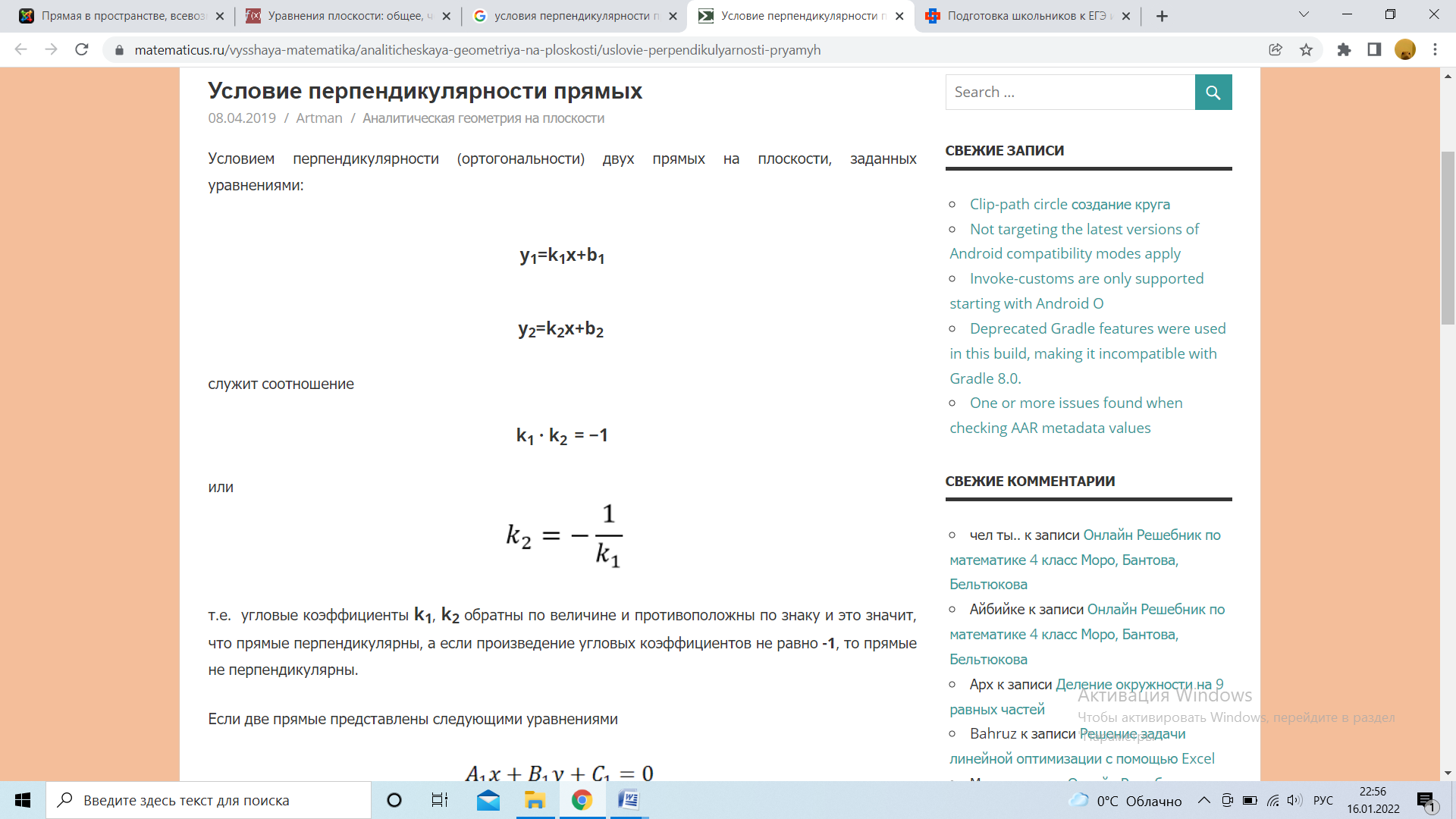   Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (график её симметричен относительно центра координат). Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (график её симметричен относительно оси ординат)  |