реферат по высшей математике. реферат. Реферат по дисциплине Математика. по теме Основные характеристики функций. Линейная функция. Линейная интерполяция и линейная экстраполяция.

Название	Реферат по дисциплине Математика. по теме Основные характеристики функций. Линейная функция. Линейная интерполяция и линейная экстраполяция.
Анкор	реферат по высшей математике
Дата	31.03.2022
Размер	0.85 Mb.
Формат файла
Имя файла	реферат.docx
Тип	Реферат #432470
страница	1 из 4

1 2 3 4

^{Федеральное государственное бюджетное образовательное учреждение высшего образования}

«Ковровская государственная технологическая академия имени В.А. Дегтярева»

Кафедра Экономики и гуманитарных наук (ЭиГН)
РЕФЕРАТ

по дисциплине: «Математика».

по теме: «Основные характеристики функций. Линейная функция. Линейная интерполяция и линейная экстраполяция.»
Руководитель:

Преподаватель Марихов И.Н.

Исполнитель

ст.гр. Вэ(БТ) – 121 Безрукова Е.Ф.
2021

Содержание
1. Основные характеристики функций.

1.1. Основные понятия

1.2. Линейная функция

1.3. Квадратичная функция

1.4. Степенная функция

1.5. Дробно – линейная функция

1.6. Показательная функция

1.7. Логарифмическая функция

2. Линейная интерполяция.

3. Линейная экстраполяция.

Список используемой литературы.

1.Основные характеристики функций.

Основные понятия

ОПРЕДЕЛЕНИЕ. Переменная величина ^yназывается функцией переменной величины x , если каждому численному значению xиз множества Xсоответствует единственное определенное значение yиз множества Y: y fx , x  X , y Y. Переменная величина xназывается независимой переменной или аргументом. Множество Xназывается областью определения функции (ООФ) или областью допустимых значений аргумента (ОДЗ). Множество Yизменения функции называется областью значений функции (ОЗФ).

^{ОПРЕДЕЛЕНИЕ. Графиком}^{функции}y  f x ^{называется множество точек}плоскости xOy , координаты которых связаны соотношением y  f x . Нули функции y  f x ^{– точки}^x^^X^,^при^{которых}^{функция}^{обращается}^в^ноль,^т.е.корни уравнения fx  0 .

^{ОПРЕДЕЛЕНИЕ.}^{Функция}fx ^с^{областью}^{определения}^X^{называется}

четной, если для любого x Xвыполняется равенство fx  fx.

Из определения четной функции следует, что ее график симметричен относительно оси ординат.

Например, функции y x² , y x являются четными, их графики имеют вид: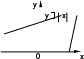

y

y x²

^y0

^–^x0 ⁰^x0 ^x
ОПРЕДЕЛЕНИЕ. Функция f x с областью определения Xназывается ^{нечетной}^,^если^для^любого^x^^X^{выполняется}^{равенство}^f ^x ^^^f^^x ^.График нечетной функции симметричен относительно начала координат.

Например, функции вид:

y x³ и y 2x являются нечетными, их графики имеют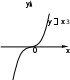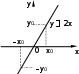

Функция, в которой переменные x и y поменялись своими ролями,

называется обратной по отношению к первоначальной функции. В свою очередь первоначальная функция является обратной к полученной.

Свойство графиков взаимно обратных функций: один получается из другого зеркальным отражением относительно биссектрисы первого и третьего координатных углов, т.е. линии y x.

^{Множество}^{значений}^{обратной}^{функции}y  f ^¹x ^{совпадает}^с^{областью}определения функции y fx , а область определения обратной функции y f^¹x ^{совпадает}^со^{множеством}^{значений}^{функции}^y^^f^^x^^.

1 2 3 4