реферат по высшей математике. реферат. Реферат по дисциплине Математика. по теме Основные характеристики функций. Линейная функция. Линейная интерполяция и линейная экстраполяция.

• Название: Реферат по дисциплине Математика. по теме Основные характеристики функций. Линейная функция. Линейная интерполяция и линейная экстраполяция.
• Анкор: реферат по высшей математике
• Дата: 31.03.2022
• Размер: 0.85 Mb.
• Имя файла: реферат.docx
• Тип: Реферат; #432470
• страница: 3 из 4

1.5.Дробно–линейная функция

ОПРЕДЕЛЕНИЕ. Функция вида

ad bc, называется дробно-линейной.

y ^{ax b}, где

cx  d

a, b, c, d – постоянные, c  0 ,

1. 
   Область определения функции _{x, d/c∪ d/c,.}
   
2. 
   Для построения графика преобразуем функцию, выделив в ее выражении
   

целую часть следующим образом.

Преобразуем тождественно числитель, чтобы выделить в нем слагаемое, содержащее знаменатель

ax b ^acx d ^ad_{ b;}

c c

поделив это выражение почленно на cx d , получим

y ^a

c

ad_{ b}

^c  ^a

^{cx d} c

bcad

_c2 _,

x ^d

c

таким образом, обозначая ^{a n,}

c

^d m,

c

k ^{bc ad}, видим, что

_c2

y ^{ax b} n

cx d

k


x m

, где

n– целая часть исходного выражения.

График дробно-линейной функции получается

сдвигом графика гиперболы ^{y k}

x

на m единиц вдоль

оси Oxи на nединиц вдоль оси Oy. Прямые y nи x m

являются асимптотами гиперболы. ^x

ПРИМЕР. Постройте график функции

_y 2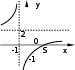x 1 _.

x  1

Запишем эту функцию так: ^{y 2 3 . Графиком функции}

x  1

будет гипербола, центр которой находится в точке  1, 2 , асимптоты - x 1 , y 2 .

1.6.Показательная функция y a^x a  0, a 1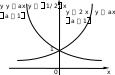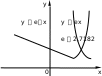






ОПРЕДЕЛЕНИЕ. Функция вида y a^x, где a – некоторое положительное ^{число, не равное единице} a 0, ^{a  1 , называется показательной.}

1. 
   Область определения функции
   
2. 
   Множество значений функции
   

x   ,  .

y 0,   .

3. 
   При x 0 значение функции y 1 .
   
4. 
   При a  1 функция возрастает на всей числовой оси; если x  0 , то y a^x 1 ; если x 0 , то 0  a^x 1 .
   
5. 
   При 0  a 1 функция убывает на всей числовой оси; если x 0 , то 0  a^x 1 ;
   

если x 0 , то a^x 1 .

1.7.Логарифмическая функция y log_a x( a 0 , a 1 )

ОПРЕДЕЛЕНИЕ. Функция, обратная показательной функции, называется

логарифмической: y log_ax.

1. 
   Область определения функции
   
2. 
   Множество значений функции
   

x 0,  .

y  ,  .

3. 
   При
   
4. 
   При
   

x 1

a 1

y log_ax 0 .

^{функция возрастает; если} 0  x 1 , то log_ax 0 , если x 1 , то

log_ax 0 .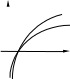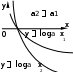

5. 
   При 0  a 1 функция убывает; если
   

y
0  x 1 , то log_ax 0 , если x 1 ,то log_ax  0 .