реферат по высшей математике. реферат. Реферат по дисциплине Математика. по теме Основные характеристики функций. Линейная функция. Линейная интерполяция и линейная экстраполяция.

• Название: Реферат по дисциплине Математика. по теме Основные характеристики функций. Линейная функция. Линейная интерполяция и линейная экстраполяция.
• Анкор: реферат по высшей математике
• Дата: 31.03.2022
• Размер: 0.85 Mb.
• Имя файла: реферат.docx
• Тип: Реферат; #432470
• страница: 4 из 4

2. Линейная интерполяция.

Интерполяция– способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.

Пусть в ходе эксперимента при изменении входной величины х(x₀, x₁, x₂, ... , x_n) получены значения функции y= f(x) в виде табличных значений (y₀,y₁,y₂, …, y_n).

Таблица 4.1. Вид таблицы экспериментальных данных

x0	x1	x2	…	xn-1	xn
y0	y1	y2	…	yn-1	yn

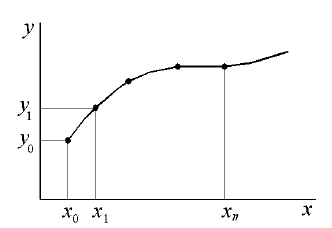Нахождение приближенной функции называется интерполяцией, а точки x₀, x₁, x₂, …, x_n – узлами интерполяции.

Графически задача интерполирования заключается в том, чтобы построить такую интерполирующую функцию, которая бы проходила через все узлы интерполирования.

Интерполяцию функций применяют в случае, когда требуется найти значение функции y(х) при значении аргумента x_i, принадлежащего интервалу [x₀, _…, x_n], но не совпадающего по значению ни с одним значением, приведенным в таблице 1.

Данная задача, а именно интерполяция функций, часто встречается при ограниченности возможностей при проведении эксперимента. В частности из-за дороговизны и трудоемкости проведения эксперимента размер выборки (x₀, x₁, x₂,..., x_n) может быть достаточно мал.

При этом во многих случаях аналитическое выражение функции y(x) не известно и получить его по таблице ее значений (табл. 1) в большинстве случаев невозможно. Поэтому вместо нее строят другую функцию, которая легко вычисляется и имеет ту же таблицу значений (совпадает с ней в точках x₀, x₁, x₂,..., x_n), что и f(x), т. е.

где i= 0, 1, 2, … , n.

P_n(x₀)=f(x₀)=y₀;

… (1)

P_n(x_i)=f(x_i)=y_i;

Нахождение приближенной функции называется интерполяцией, а точки x₀, x₁, x₂, …, x_n– узлами интерполяции.

Интерполирующую функцию ищут в виде полинома nстепени.

Для каждого набора точек имеется только один интерполяционный многочлен, степени не больше n. Однозначно определенный многочлен может быть представлен в различных видах.

Графически задача интерполирования заключается в том, чтобы построить такую интерполирующую функцию, которая бы проходила через все узлы интерполирования (рис. 1).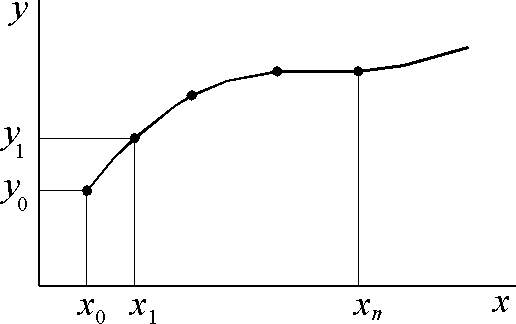

Рис. 1. Вид интерполирующей функции

Линейная интерполяция – простейший и часто используемый вид интерполяции. Она состоит в том, что заданные точки с координатами x_i, y_iпри i=0, 1, 2, ... n соединяются прямолинейными отрезками, а функцию y(x) можно приближенно представить в виде ломаной.

Уравнения каждого отрезка ломаной в общем случае разные. Поскольку имеется n интервалов (x_i-1, x_i), то для каждого из них в качестве уравнения интерполяционного многочлена используется уравнение прямой, проходящей через две точки: для i-го интервала можно написать уравнение прямой, проходящей через точки (x_i-1, y_i-1) и (x_i, y_i),

Отсюда

y - y_{i -1} ^yi^{- y}i-1

₌ x-x_{i-1 .}

^xi^{- x}i-1

y=a_ix+b_i, x_{i-1 ≤} x_≤ x_i; (4)

a_i=

^{yi- yi-1} , b_i=y_i-1 –a_i x_i-1. (5)

^xi^{- x}i-1

Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента x, а затем подставить его в формулу (4) и найти приближенное значение функции в этой точке. Пример линейной интерполяции для экспериментальных данных согласно табл. 2. приведен на рис. 2.

Таблица 2

Таблица экспериментальных данных

Индекс	0	1	2	3	4
x	1	2	3	4	5
y	2,5	4	3,5	5	6

7



y

6

5

4

3

2

1

0


6
0 1 2 3 4 5 ^x

Рис. 2. Графическое решение линейной интерполяции

3. Линейная экстраполяция.

В математике экстраполяция — это разновидность аппроксимации, при которой оценивание значения переменной производится не внутри интервала её изменения (интерполяция), а вне его. При этом экстраполяция в большей степени, чем интерполяция подвержена влиянию неопределённости и риску получить некорректные результаты.

В анализе данных основное применение экстраполяции — прогнозирование. Экстраполяционные методы являются одними из самых распространенных и наиболее разработанных среди всей совокупности методов прогнозирования.

Фактически, экстраполяция — это попытка распространить наблюдаемые в прошлом зависимости в данных, на будущее. Поэтому с точки зрения бизнеса это и есть задача прогнозирования, а экстраполяция — один из механизмов её решения.

Существует несколько методов экстраполяции, выбор наиболее подходящего из которых зависит от априорных сведений о процессе, который сформировал наблюдаемые точки данных — является ли функция гладкой, непрерывной или периодической. Методы экстраполяции, в основном, те же самые, что и интерполяции.

Наиболее простым из методов является линейная экстраполяция. Она даёт хорошие результаты в том случае, если сама исходная функция близка к линейной, а экстраполируемая точка расположена недалеко от последней наблюдаемой точки данных xn.

Пусть экстраполируется точка (xn+1,yn+1). Ближайшими к ней точками наблюдаемых данных будут (xn−1,yn−1) и (xn,yn). Тогда линейная экстраполирующая функция будет иметь вид:

y(xn+1)=xn−1+xn+1−xn−1xn−xn−1(yn−yn−1).

Таким образом, при линейной экстраполяции, новая точка (xn+1,yn+1) строится так, как если бы по ней и точке (xn−1,yn−1) интерполировалась бы точка (xn,yn).



Если для экстраполяции используется больше двух точек, то угловой коэффициент итоговой интерполирующей прямой может быть определён путём усреднения.

С точки зрения прогнозирования линейная модель экстраполяции является довольно грубой и приближённой, особенно если исходная функция существенно нелинейная, отсчёты наблюдаемых точек ряда расположены далеко друг от друга или экстраполируемая точка расположена далеко от последнего наблюдаемого значения данных. В этом случае предпочтительно использовать полиномиальную экстраполяцию.

Однако линейная экстраполяция является достаточно простой в реализации и понимании, что делает её актуальной во многих практических случаях прогнозирования.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1.Высшая математика для экономистов: учебник / Под ред. проф. Н.Ш. Кремера. - 3-е изд. - М. : ЮНИТИ-ДАНА, 2010.

2. Высшая математика для экономистов : практикум / Под ред. проф. Н.Ш. Кремера. - 2-е изд., перераб. и доп. - М. : ЮНИТИ-ДАНА, 2010.

3.Конспект лекций по высшей математике. Полный курс : учебное пособие / Д. Т. Письменный. - 8-е изд. - М. : Айрис-пресс, 2009.

4.Математика: учебник для бакалавров / Н.В. Богомолов, П.И. Самойленко. - 5-изд. - М. : Юрайт, 2012.

5.Высшая математика: учебник / В.А. Ильин, А.В. Куркина. - 3-е изд., перераб. - М. : Проспект, 2011.

6.Сборник задач по курсу математического анализа : учебное пособие / Г.Н. Берман. - 22-е изд., перераб. - СПб. : Профессия, 2008..

7.Сборник задач по математике для втузов: в 4-х частях. Ч.1 : Линейная алгебра и основы математического анализа : учеб. пособие для втузов / Под общ. ред. А.В. Ефимова, Б.П. Демидовича. - 6-е изд., стереотип. - М. : Альянс, 2011.