реферат по высшей математике. реферат. Реферат по дисциплине Математика. по теме Основные характеристики функций. Линейная функция. Линейная интерполяция и линейная экстраполяция.
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
Линейная функцияЛинейной функцией называется функция вида y = kx + b, заданная на множестве всех действительных чисел. Здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная. В частном случае, если k = 0, получим постоянную функцию y = b, график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами (0; b). Если b = 0, то получим функцию y = kx, которая является прямой пропорциональностью. Геометрический смысл коэффициента b – длина отрезка, который отсекает прямая по оси Oy, считая от начала координат. Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки. Свойства линейной функции: 1) Область определения линейной функции есть вся вещественная ось; 2) Если k ≠ 0, то область значений линейной функции есть вся вещественная ось. Если k = 0, то область значений линейной функции состоит из числа b; 3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b. a) b ≠ 0, k = 0, следовательно, y = b – четная; b) b = 0, k ≠ 0, следовательно y = kx – нечетная; c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида; d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция. 4) Свойством периодичности линейная функция не обладает; 5) Точки пересечения с осями координат: Ox: y = kx + b = 0, x = -b/k, следовательно (-b/k; 0) – точка пересечения с осью абсцисс. Oy: y = 0k + b = b, следовательно (0; b) – точка пересечения с осью ординат. Замечание.Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х. Если b ≠ 0 и k = 0, то функция y = b не обращается в ноль ни при каких значениях переменной х. 6) Промежутки знакопостоянства зависят от коэффициента k. a) k > 0; kx + b > 0, kx > -b, x > -b/k. y = kx + b – положительна при x из (-b/k; +∞), y = kx + b – отрицательна при x из (-∞; -b/k). b) k < 0; kx + b < 0, kx < -b, x < -b/k. y = kx + b – положительна при x из (-∞; -b/k), y = kx + b – отрицательна при x из (-b/k; +∞). c) k = 0, b > 0; y = kx + b положительна на всей области определения, k = 0, b < 0; y = kx + b отрицательна на всей области определения. 7) Промежутки монотонности линейной функции зависят от коэффициента k. k > 0, следовательно y = kx + b возрастает на всей области определения, k < 0, следовательно y = kx + b убывает на всей области определения. 8) Графиком линейной функции является прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b. Ниже приведена таблица, которая наглядно это иллюстрирует рисунок 1 . 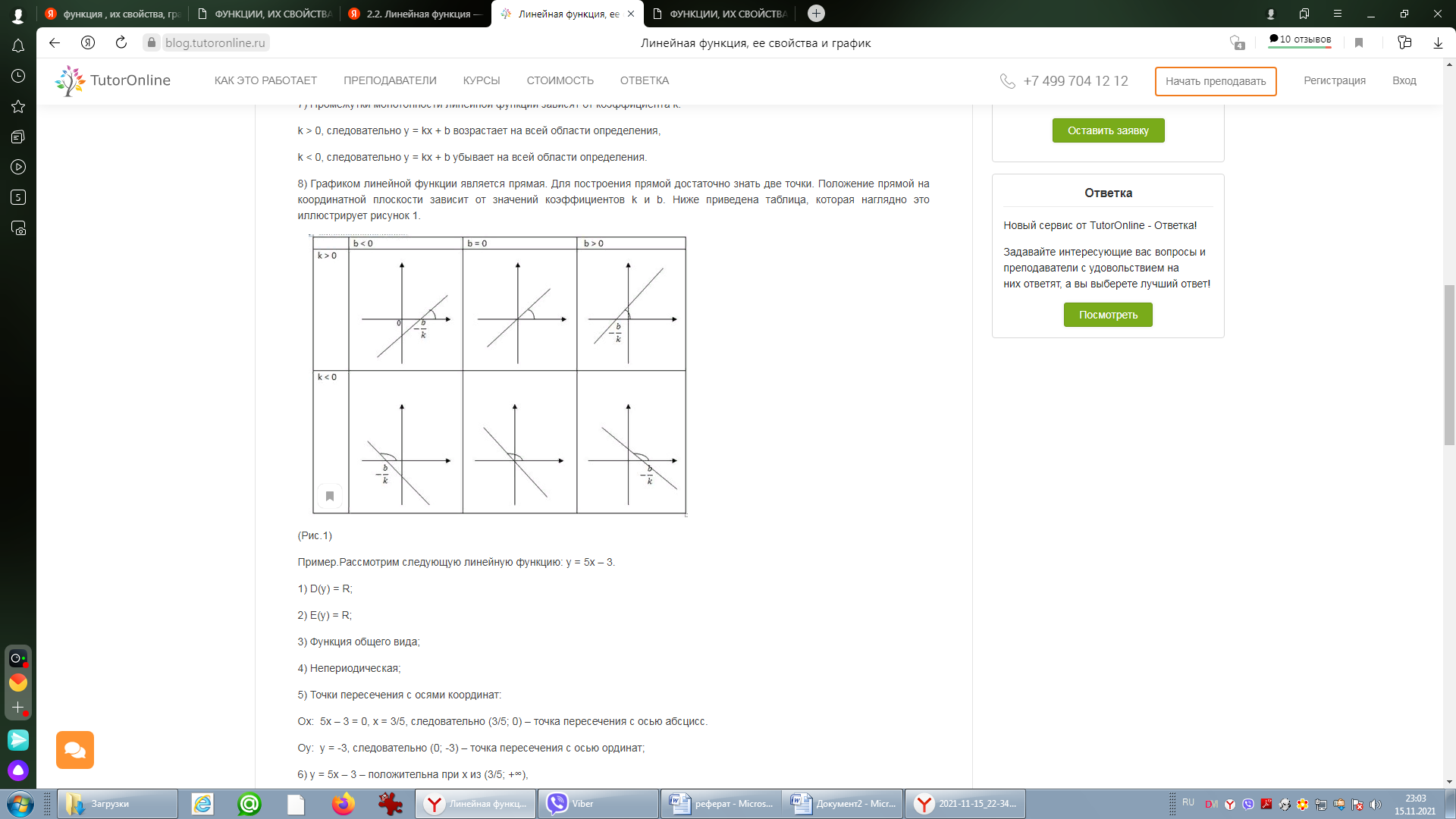 (Рис.1) (Рис.1)Пример. Рассмотрим следующую линейную функцию: y = 5x – 3. 1) D(y) = R; 2) E(y) = R; 3) Функция общего вида; 4) Непериодическая; 5) Точки пересечения с осями координат: Ox: 5x – 3 = 0, x = 3/5, следовательно (3/5; 0) – точка пересечения с осью абсцисс. Oy: y = -3, следовательно (0; -3) – точка пересечения с осью ординат; 6) y = 5x – 3 – положительна при x из (3/5; +∞), y = 5x – 3 – отрицательна при x из (-∞; 3/5); 7) y = 5x – 3 возрастает на всей области определения; 8) 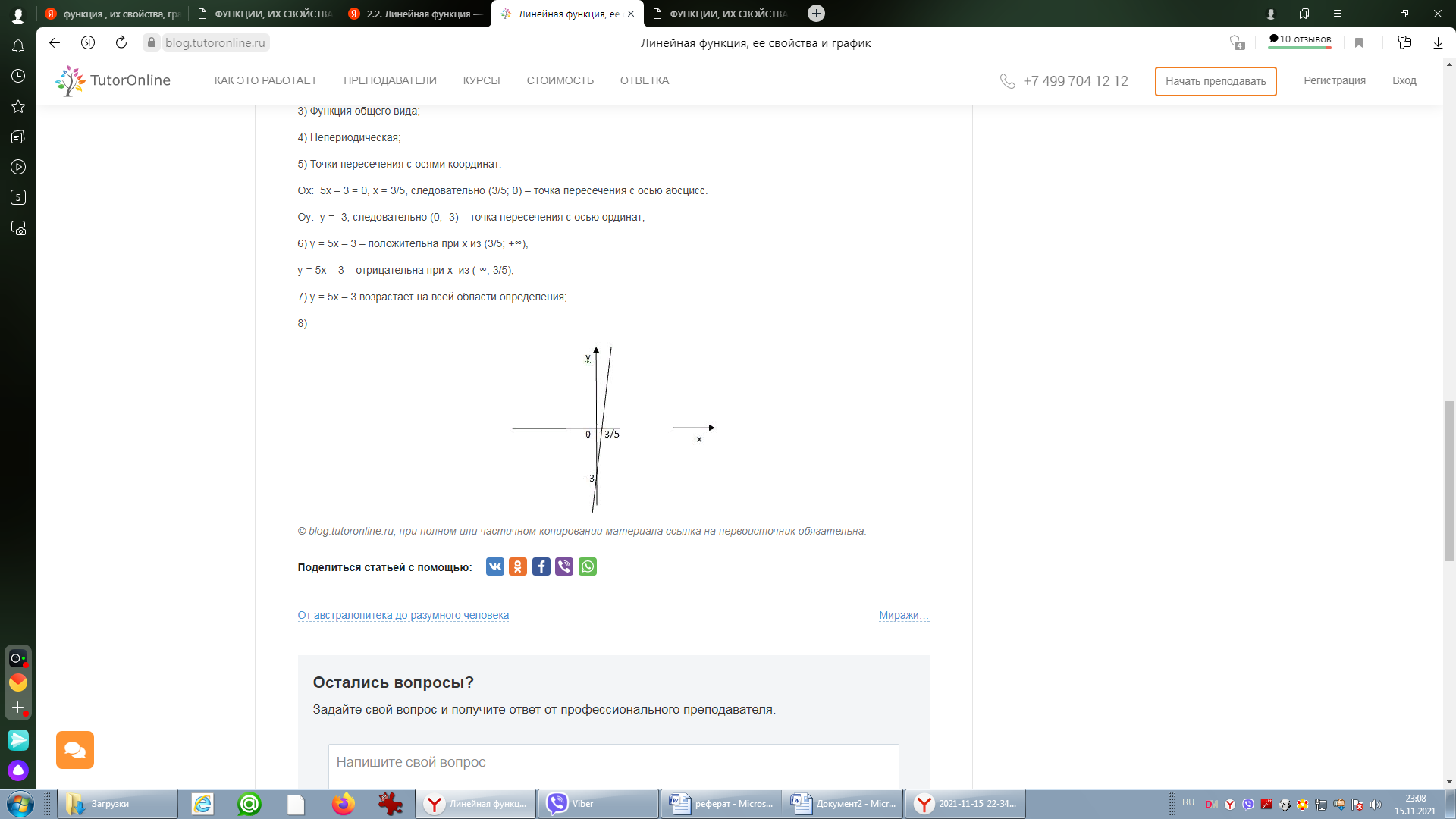 1.3.Квадратичная функция. Это функция вида Графиком  Парабола В общем случае вершина лежит в точке 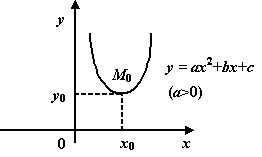 .Парабола с вершиной в точке Область определения квадратичной функции – вся числовая прямая. При b0 функция не является четной и не является нечетной. При b=0 квадратичная функция – четная.   f(x) = x2 y 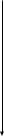   f(x) = (x+1/2)2 y 0 x Рис. 4 Рис. 5 Квадратичная функция непрерывна и дифференцируема во всей области определения. Функция имеет единственную критическую точку x=-b/(2a). Если a>0, то в точке x=-b/(2a) функция имеет минимум. При x<-b/(2a) функция монотонно убывает, при x>-b/(2a) монотонно возрастает. Если а<0, то в точке x=-b/(2a) функция имеет максимум. При x<-b/(2a) функция монотонно возрастает, при x>-b/(2a) монотонно убывает. Точка графика квадратичной функции с абсциссой x=-b/(2a) и ординатой y= -((b2-4ac)/4a) называется вершиной параболы. Область изменения функции: при a>0 – множество значений функции [-((b2-4ac)/4a); +); при a<0 – множество значений функции (-;-((b2-4ac)/4a)]. График квадратичной функции пересекается с осью 0y в точке y=c. В случае, если b2-4ac>0, график квадратичной функции пересекает ось 0x в двух точках (различные действительные корни квадратного уравнения); если b2-4ac=0 (квадратное уравнение имеет один корень кратности 2), график квадратичной функции касается оси 0x в точке x=-b/(2a); если b2-4ac<0, пересечения с осью 0x нет. Из представления квадратичной функции в виде (1) также следует, что график функции симметричен относительно прямой x=-b/(2a) – образа оси ординат при параллельном переносе r=(-b/(2a); 0). График функции f(x)=ax2+bx+c (или f(x)=a(x+b/(2a))2-(b2-4ac)/(4a)) может быть получен из графика функции f(x)=x2 следующими преобразованиями: а) параллельным переносом r=(-b/(2a); 0); б) сжатием (или растяжением) к оси абсцисс в а раз; в) параллельным переносом r=(0; -((b2-4ac)/(4a))). 1.4.Степенные функции y x y xn n N ОПРЕДЕЛЕНИЕ. Функция вида y xn , n N , называется степенной функцией с натуральным показателем. Область определения функции (n– четное) (n– нечетное) 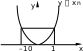 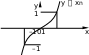 D y0,. Dy , Функция является четной при четном nи нечетной при нечетном n. Если n нечетно, то функция y xn возрастает при x , ; если nчетно, то функция y xnвозрастает при x0, и убывает при x , 0. y xn1 n N xn  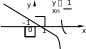 Функция непрерывна на , . Функция непрерывна на , . ( n– четное) ( n– нечетное) ОПРЕДЕЛЕНИЕ. Функция вида y xn называется степенной функцией с целым отрицательным показателем. Область определения функции – x ,0∪ 0, . Функция является четной при четном nи нечетной при нечетном n. Функция убывает при возрастает, если nчетное. x 0 ; при x 0 функция убывает, если nнечетное, и Функция непрерывна на , 0 функции. и на 0, ; x 0 – точка разрыва Обратной пропорциональностью называется функция, заданная формулой y k, где x k 0 . Область определения x ,0∪ 0,. Область значений x ,0∪ 0,. График не проходит через начало координат. y k x нечетная функция (поскольку f x k x k fx. График этой x функции симметричен относительно начала координат. 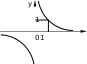 Если k 0 , то функция y k Если k 0 , то функция y kx убывает на промежутке 0, и на промежутке , 0 . Если 19 k 0 , x то функция y k x возрастает на промежутке , 0 и на промежутке 0, . Точек пересечения с осями координат не существует. При При k 0 k 0 y 0 y 0 на 0, , на , 0 , y 0 y 0 на , 0 . на 0, . Функция непериодическая. Если k 0 , то ветви графика расположены в II и IV координатных 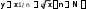 четвертях. Графиком обратной пропорциональности гипербола. четвертях. Графиком обратной пропорциональности гипербола.y k, x k 0 является 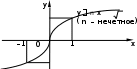   Функция y является обратной к функции y xn. Отразив график функции Функция y является обратной к функции y xn. Отразив график функции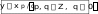    y xnсимметрично относительно прямой y x,получим график функции y . y xnсимметрично относительно прямой y x,получим график функции y . |
