4-лекция. НОК и НОД. Нод и нок чисел
 Скачать 47.11 Kb. Скачать 47.11 Kb.
|
|
4-лекция. Тема: НОД и НОК чисел. План занятия: 1. Общие кратные и НОК чисел. 2. Общие делители и НОД чисел. 3. Основная теорема арифметики. 4. Алгоритмы нахождения НОК и НОД данных чисел. Ключевые слова: общие кратные, общие делители, основная теорема арифметики, алгоритмы НОК и НОД чисел, каноническое разложение. 1. Общие кратные и НОК чисел. Определение. Если число а делится на число b, то а называют кратным числа b. Множество кратных числа b бесконечно. Общий вид чисел, кратных b, есть nb, где n произвольное натуральное число. Наименьшее число этого множества есть само b. Определение. Если число m является кратным чисел а и b, то его называют их общим кратным. Определение. Наименьшее из общих кратных чисел а и b называют наименьшим общим кратным этих чисел и обозначают как НОК(а;b) (кратко К(а; b)). Например, пусть множеством кратных числа 6 является A= {6, 12, 18, 24, 30, 36, 42, 48, 54, ...}, множеством кратных числа 8 является B ={8, 16, 24, 32, 40, 48, 56, ...}. Множество общих кратных этих чисел есть A∩B ={24, 48, 72, ...} и наименьший из них есть число 24 = НОК(6, 8). Свойства наименьшего общего кратного. 1°. Любое ОК (а,в) делится на НОК (а,в). Доказательство. Пусть m⋮a ∧ m  ⋮ b ∧ K(a, b) = k. Для доказательства m⋮ k, предположим обратное, т.е. пусть число m делится на k с остатком: m = kq+ r (r <k). m ⋮ a ∧ k⋮ a ⋮ b ∧ K(a, b) = k. Для доказательства m⋮ k, предположим обратное, т.е. пусть число m делится на k с остатком: m = kq+ r (r <k). m ⋮ a ∧ k⋮ a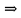 r = (m - kq) ⋮ a (по теореме о делимости разности). Так же (m⋮ b ∧ k⋮ b) ⇒ r = (m - kq) ⋮ b; (r⋮ a∧r⋮ b) ⇒ r=ОK(a,b). Т.к. k = K(a, b) то ОК (а,в) = r > k. Но остаток r не может превосходить делителя, это противоречие показывает, что r= 0. r = (m - kq) ⋮ a (по теореме о делимости разности). Так же (m⋮ b ∧ k⋮ b) ⇒ r = (m - kq) ⋮ b; (r⋮ a∧r⋮ b) ⇒ r=ОK(a,b). Т.к. k = K(a, b) то ОК (а,в) = r > k. Но остаток r не может превосходить делителя, это противоречие показывает, что r= 0.2°. Если НОК (a, b) = k, то для ∀с∈N НОK(ac, bc) = kc. Доказательство. 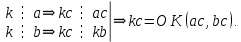 Теперь докажем, что kc является НОК(ac, bc). Допустим, что НОК(ac, bc)= 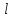 . Пусть . Пусть 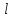 <kc. Из того, что <kc. Из того, что 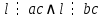 следует что следует что 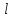 :c<kc:c= k, т.е. :c<kc:c= k, т.е. 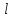 :c<k, Вместе с тем ( :c<k, Вместе с тем (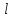 :c)⋮ a∧( :c)⋮ a∧(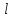 :c)⋮ b, это противоречит предположению НОК(ac, bc)=l. Получается что (l:c)= НОК (a,b). Следовательно, наше предположение неверно. :c)⋮ b, это противоречит предположению НОК(ac, bc)=l. Получается что (l:c)= НОК (a,b). Следовательно, наше предположение неверно.2. Общие делители и НОД чисел. Определение. Если число а делится на число b, то b называют делителем числа a. Множество делителей числа а конечно. Наибольшее число этого множества есть само a, наименьшее – число 1. Определение. Если число m является делителем чисел а и b, то его называют их общим делителем. Определение. Наибольшее из общих делителей чисел а и b называют наибольшим общим делителем этих чисел и обозначают как НОД (а; b) (кратко Д(а; b)). Например, множество делителей числа 24: A = {1, 2, 3, 4, 6, 8, 12, 24}, а множество делителей числа 36: B= {1, 2, 3, 4, 6, 9, 12, 18, 36}, их общие делители A ∩ B = {1, 2, 3, 4, 6, 12}. Наибольшее из общих делителей равен 12, т.е. 12= НОД (24, 36). Свойства наибольшего общего делителя. 1°. Если c = ОД(a,b), то l = 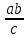 = ОК(a,b), то есть, если c является общим кратным чисел a,b, то l = = ОК(a,b), то есть, если c является общим кратным чисел a,b, то l =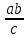 будет их общим кратным. будет их общим кратным.Доказательство. Покажем, что l⋮a∧l⋮b. Из c = ОД(a, b)⇒a⋮c ⇒ a = a1c ∧ b⋮c⇒b = b1c; 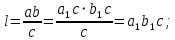 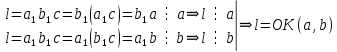 . .2°.Если 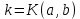 , то, , то, 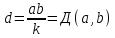 . .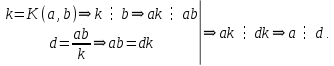 Таким же образом можно показать, что b⋮d, следовательно, d = ОД(a, b). Теперь покажем, что d=НОД(a, b). Предположим, что у чисел a и b есть общий делитель с, больше, чем d. Тогдa, по 1-свойству 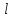 = =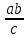 =OK(a, b);c>d⇒ =OK(a, b);c>d⇒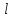 = = = =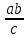 < <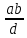 =k⇒ =k⇒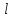 <k. Таким образом, общее кратное чисел а и b стало меньше, чем их НОК. Это противоречие показывает ложность нашего предположения. Следовательно, d=НОД(a,b). <k. Таким образом, общее кратное чисел а и b стало меньше, чем их НОК. Это противоречие показывает ложность нашего предположения. Следовательно, d=НОД(a,b).Следствия: 1) Д(a, b)⋅К(a, b) = 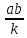 ⋅k = ab. ⋅k = ab.2) Если Д(a, b) = 1, то K(a,b) = ab. 3)НОД (a,b) делится на любой из их общих делителей. 4) (Д(b,c) = l ∧ a⋮b∧a⋮c)⇒(a⋮bc). Доказательство. a⋮b∧a⋮c⇒ a = ОК(b, c)⇒ a⋮НОД(b,c). Д(b, c) =1⇒ K(b, c) = bc . Следовательно, a⋮bc. Из 3- и 4-следствий вытекает признак делимости на составное число. Это составное число должно состоять из произведения не менее двух взаимно простых чисел. Приведем в пример некоторые из них. Признак делимости на 6: Для того чтобы число делилось на 6, достаточно, чтобы оно делилось на 2 и на 3. Признак делимости на 12: Для того чтобы число делилось на 12, достаточно, чтобы оно делилось на 4 и на 3. Признак делимости на 15: Для того чтобы число делилось на 15, достаточно, чтобы оно делилось на 5 и на 3. 3. Основная теорема арифметики. Каждое натуральное число, большее единицы, представимо в виде произведения простых чисел, причём единственным способом с точностью до порядка следования сомножителей. Доказательство. Применим к натуральному числу а теорему 5 из п. 9.3.2, которая утверждает, что у числа а есть простой делитель р1, т. е. а = р1q. Затем ту же теорему применим к числу q, т. е. q = p2r, где р2 - тоже простое число. Получаем a=p1p2r. Продолжая этот процесс далее, через конечное число шагов получим а=р1×р2...рk, где все pi— простые числа. Докажем, что это разложение единственно. Для этого применим метод математической индукции, опираясь на принцип наименьшего натурального числа. Предположим, что существуют натуральные числа, разлагающиеся в произведение простых чисел хотя бы двумя различными способами. Тогда среди таких чисел существует наименьшее, пусть это будет число а, т. е. а = р1×р2...рk = q1q2...qn, где все pвсе р и все q— простые числа, k>1,n>1. Заметим, что k = 1или п = 1 не может, ибо в этом случае число а было бы простым, а единственность разложения простого числа на простые множители очевидна. Тогда q1q2...qn 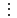 p1 и найдется такое qi = р1,ибо qi -простое число и делится только на себя и на единицу, но p1>1. Используя свойство 6 (7.6.2), можем сократить равенство на число р1. Получим:р2 ... рk = q1q2 ... qi-1qi+1 … qn = p1 и найдется такое qi = р1,ибо qi -простое число и делится только на себя и на единицу, но p1>1. Используя свойство 6 (7.6.2), можем сократить равенство на число р1. Получим:р2 ... рk = q1q2 ... qi-1qi+1 … qn = 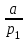 . .Но число 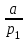 < а, ибо p1>1.Поэтому по предположению индукции для числа < а, ибо p1>1.Поэтому по предположению индукции для числа 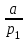 теорема верна и каждое р, начиная с р2, равно некоторому q, а также число множителей в обеих частях равенства совпадает. Получили k - l= n - l, откуда k = n. теорема верна и каждое р, начиная с р2, равно некоторому q, а также число множителей в обеих частях равенства совпадает. Получили k - l= n - l, откуда k = n. Так как еще ранее было показано, что р1 = qi, то оба разложения числа а если и отличаются друг от друга, то только порядком следования множителей, т. е. для числа а теорема верна. Получили противоречие с предположением, следовательно, теорема верна для всех натуральных чисел. Основная теорема арифметики позволяет представлять натуральное число в виде произведения степеней различных простых чисел и использовать единственность этого разложения. Мы часто пользуемся разложением натуральных чисел в произведение простых множителей. Например, запись 110 = 2×5×11 говорит о том, что число 110 разложено на простые множители 2, 5, 11. Разложить на простые множители можно всякое составное число, при чём при любом способе получается одно и то же разложение, если не учитывать порядка множителей. Поэтому представление числа 110 в виде произведения 2×5×11 или произведение 5×2×11 есть по существу одно и то же разложение числа 110 на простые множители. Обычно простые множители, входящие в разложение натурального числа а, пишут в порядке возрастания. При этом среди таких множителей могут встречаться повторяющиеся, тогда произведение повторяющихся множителей записывают с помощью обозначения степени. Разложение числа а= 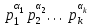 , где р1<р2< … <рk -различные простые числа, называется каноническим разложением или каноническим видом числа а. , где р1<р2< … <рk -различные простые числа, называется каноническим разложением или каноническим видом числа а.Например, 24 = 23× 3; 30 = 2 × 3 × 5; 2100 = 22× 3 × 52× 7. Каждое натуральное число большее 1, имеет единственное каноническое разложение на множители (в каноническом разложении нельзя даже переставлять множители, так как тогда простые числа не будут идти в порядке возрастания). Не теряя общности, можно считать, что в разложение а =  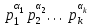 , входят все простые числа от а до рk, если какое-нибудь простое число не входит в это разложение, его пишут с нулевым показателем. , входят все простые числа от а до рk, если какое-нибудь простое число не входит в это разложение, его пишут с нулевым показателем.Например: 726=2×3×112=2×3×50×70×112. Раскладывая числа на простые множители, используют признаки делимости на 2,3,5 и другие. Разложим число 720 на простые множители. Число 720 делится на 2, значит 2 есть один из простых множителей в разложении числа 720. Разделим 720 на 2. Число 2 пишем справа от знака равенства, а частное 360 – под числом720. Число 360делим на 2, получаем 180. Делим 180 на 2, получим 90.Потом делим 90 на 2, получим 45. Делим 45 на 3, получим 15.Делим 15 на 3, получим 5. Число 5 – простое, при делении его на 5 получаем 1. Разложение на множители завершено. Произведение одинаковых множителей заменим степенью. 720=2·2·2·2·3·3·5=24·32·5. 360 180 90 45 15 5 1 720=24·32·5 это и есть каноническое разложение числа 720. 3.4. Алгоритмы нахождения НОК и НОД данных чисел. Нахождение наименьшего общего кратного нескольких чисел способом разложения на простые множители Чтобы найти наименьшее общее кратное данных чисел: 1. Представляем каждое данное число в каноническом виде; 2. Образуем произведение из всех простых множителей, находящихся в разложениях данных чисел, причем каждый берем с наибольшим показателем, с каким он входит во все разложения данных чисел; 3. Находим значение этого произведения — оно и будет наименьшим общим кратным данных чисел. Нахождение наименьшего общего кратного нескольких чисел способом разложения на простые множители Чтобы найти наименьшее общее кратное данных чисел: 1. Представляем каждое данное число в каноническом виде; 2. Образуем произведение из всех простых множителей, находящихся в разложениях данных чисел, причем каждый берем с наибольшим показателем, с каким он входит во все разложения данных чисел; 3. Находим значение этого произведения — оно и будет наименьшим общим кратным данных чисел. 60 = 22·3·5, 252=22·3 2·7, 264 = 23·3 ·11. 2.Образуем произведение общих для всех данных разложений простых множителей, причем каждый из них берем с наименьшим показателем, с каким он входит во все разложения данных чисел: D(60, 252, 264) = 22×3=12. 3.Находим значение этого произведения – 12 - оно и будет наибольшим общим делителем данных чисел. Пример 3. Найдем наибольший общий делитель и наименьшее общее кратное чисел 48 и 245. 1.Представим каждое число в каноническом виде: 48 =2×2×2×2×3 = 24×3, 245 =5×7×7 = 5×72. 24 49 12 7 6 1 3 1 Так как разложения данных чисел не содержат общих простых множителей, то D (48, 245)= 1, а К (48, 245) = 48× 245= 10 760. Алгоритм Евклида: 1. Если число a кратно числу b, то Д(a, b) = b, так как у числа b нет делителя превосходящего его. 2. Если число a не кратно числу b, то a = bq + r и ОД(a, b) = ОД(b, r).То есть число a делится на число b с остатком, и множество общих делителей чисел a и b совпадает с множеством общих делителей чисел b и остатка r при делении числа a на b. Пусть d=ОД(a,b). Тогда (a:d∧b:d)⇒(r=a-bq):d (по теореме о делимости разности), следовательно, d = ОД(b, r). Так же, пусть d= ОД(b,r), т.к. a=bq+r, то число a тоже делится на d по теореме о делимости суммы, следовательно, d=ОД(a, b). Наконец, если a = bq + r и a,b,r ∈ N, то НОД(a,b) = НОД(b, r). Так как множество общих делителей чисел a и b совпадает с множеством общих делителей чисел b и остатка r при делении числа a на b, то совпадают наибольшие элементы этих множеств. Пользуясь этими утверждениями можно нахождение НОД чисел a и b, заменить на нахождение НОД чисел b и r.Если b не кратно r, то, НОД(b,r) = НОД (r, r1), и так далее. Последний отличный от 0 остаток будет являться НОД(a,b). Контрольные вопросы: 1. Дайте определение НОД и НОК чисел 2. Повторите основные свойства НОД и НОК чисел 3. Сформулируйте несколько признаков делимости на составное число. 4. Обоснуйте эти признаки. 5. Расскажите алгоритмы нахождения НОК и НОД данных чисел. 6. Обоснуйте алгоритм Евклида. |
