многочлены. Курсовая яна. Нод и нок многочленов
 Скачать 96.48 Kb. Скачать 96.48 Kb.
|
2.4 Расширенный алгоритм ЕвклидаПусть алгоритм Евклида на каждом шаге, кроме частного 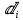 и остатка и остатка 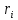 , вычисляет еще два значения , вычисляет еще два значения 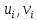 по правилу по правилу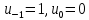 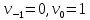 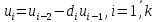 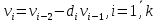 Такой алгоритм будет называться расширенным алгоритмом Евклида. В расширенном алгоритме Евклида для всех 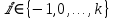 выполняется равенство выполняется равенство 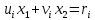 . Значение расширенного алгоритма Евклида состоит в том, что он дает линейное разложение наибольшего общего делителя . Значение расширенного алгоритма Евклида состоит в том, что он дает линейное разложение наибольшего общего делителя 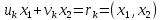 , которое играет важнейшую роль в операциях модульной арифметики. , которое играет важнейшую роль в операциях модульной арифметики.Легко показать, что длина чисел 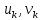 оценивается величиной оценивается величиной 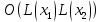 . Значит, сложность расширенного алгоритма Евклида отличается от сложности обычного алгоритма Евклида не более чем на константный множитель, т.е. для расширенного алгоритма Евклида сохраняется оценка сложности . Значит, сложность расширенного алгоритма Евклида отличается от сложности обычного алгоритма Евклида не более чем на константный множитель, т.е. для расширенного алгоритма Евклида сохраняется оценка сложности 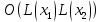 . [6] . [6]2.5 Другие алгоритмы вычисления наибольшего общего делителяРассмотрим сначала один из простейших способов ускорения работы алгоритма Евклида. Пусть в ходе выполнения алгоритма вычисляются величины    , ,   Здесь на  -м шаге алгоритма сначала вычисляется остаток от деления -м шаге алгоритма сначала вычисляется остаток от деления  на на  , 0 , 0 . Затем, если . Затем, если  , то полагаем , то полагаем  , ,  . Если же . Если же  , то полагаем , то полагаем , , В результате получаем равенство  , в котором , в котором . .Нетрудно доказать, что в описанном алгоритме  . Однако у описанного алгоритма по-другому оценивается количество шагов. Действительно, из условия . Однако у описанного алгоритма по-другому оценивается количество шагов. Действительно, из условия  , ,  следует, что следует, что  . Значит, количество шагов алгоритма . Значит, количество шагов алгоритма  не превосходит не превосходит  . Эта оценка не сколько меньше оценки, полученной в теореме 1.3 для алгоритма Евклида. Вместе с тем общая оценка сложности алгоритма . Эта оценка не сколько меньше оценки, полученной в теореме 1.3 для алгоритма Евклида. Вместе с тем общая оценка сложности алгоритма  не изменяется. не изменяется.Имеется целый ряд алгоритмов вычисления наибольшего общего делителя, в которых операция деления с остатком заменена на операцию деления с остатком на степени двойки. Поскольку данная операция для чисел  , представленных в , представленных в  -ичной системе счисления выполняется всего за -ичной системе счисления выполняется всего за  операций, то достигается выигрыш в сложности каждого шага алгоритма. Однако обычно число шагов данных алгоритмов оказывается больше числа шагов алгоритма Евклида. [3] операций, то достигается выигрыш в сложности каждого шага алгоритма. Однако обычно число шагов данных алгоритмов оказывается больше числа шагов алгоритма Евклида. [3]Для чисел  сложности таких алгоритмов вычисления сложности таких алгоритмов вычисления  обычно оценивается величиной обычно оценивается величиной  , однако экспериментальные данные свидетельствуют о том, что данные алгоритмы на 20-25% эффективнее алгоритма Евклида. , однако экспериментальные данные свидетельствуют о том, что данные алгоритмы на 20-25% эффективнее алгоритма Евклида.Пусть даны целые числа  . Опишем сначала сам LSBGCD-алгоритм. Вычисляется последовательность упорядоченных пар . Опишем сначала сам LSBGCD-алгоритм. Вычисляется последовательность упорядоченных пар  неотрицательных чисел, где неотрицательных чисел, где  , и если уже вычислена пара , и если уже вычислена пара  , то: , то:Находится число  свойством свойством 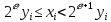 Вычисляется 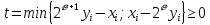 Если при этом 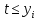 , то полагаем , то полагаем 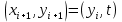 , а если , а если 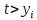 , то полагаем , то полагаем 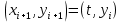 . .Алгоритм заканчивает свою работу, как только очередное значение 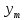 оказывается равным нулю. При этом наибольшим общим делителем чисел оказывается равным нулю. При этом наибольшим общим делителем чисел 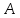 и и 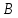 является число является число 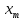 . .Убедимся в корректности приведенного алгоритма. Утверждение 1.2. Пусть даны целые числа 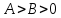 . LSBGCD алгоритм правильно вычисляет наибольший общий делитель чисел . LSBGCD алгоритм правильно вычисляет наибольший общий делитель чисел 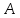 и и 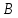 за конечное число шагов. Доказательство. Во-первых, из описания LSBGCD алгоритма нетрудно увидеть, что на за конечное число шагов. Доказательство. Во-первых, из описания LSBGCD алгоритма нетрудно увидеть, что на 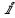 -м шаге алгоритма выполняются неравенства -м шаге алгоритма выполняются неравенства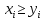 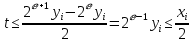 Покажем, что число шагов алгоритма конечно. Из описания LSBGCD-алгоритма видно, что 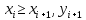 . Кроме того неравенство . Кроме того неравенство 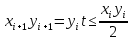 . Значит, найдется . Значит, найдется 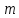 , для которого , для которого 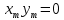 . Отсюда следует, что . Отсюда следует, что  , и LSBGCD-алгоритм выполняется за конечное число шагов. , и LSBGCD-алгоритм выполняется за конечное число шагов.Теперь индукцией по  докажем, что на каждом шаге алгоритма наибольший общий делитель чисел докажем, что на каждом шаге алгоритма наибольший общий делитель чисел  равен наибольшему общему делителю равен наибольшему общему делителю  . Равенство . Равенство  очевидно. Рассмотрим теперь пару очевидно. Рассмотрим теперь пару  . Не ограничивая общности, будем считать, что в ходе выполнения . Не ограничивая общности, будем считать, что в ходе выполнения  -го шага алгоритма не проводилась перестановка чисел в паре, т.е. -го шага алгоритма не проводилась перестановка чисел в паре, т.е.  , а , а  . Тогда . Тогда  и, следовательно, и, следовательно,  . Значит, . Значит,  . С другой стороны, из условий, . С другой стороны, из условий, 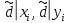 следует, что, следует, что, 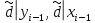 .Значит, .Значит, 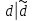 . В итоге получаем, . В итоге получаем, 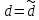 , т.е. , т.е. 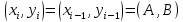 . .Воспользовавшись доказанным равенством для 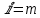 , видим, что , видим, что 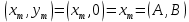 Подсчитаем сложность LSBGCD-алгоритма. Из описания алгоритма видно, что на 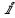 -м шаге выполняются только вычитания чисел, умножения на степень двойки, а также сравниваются между собой числа. Поэтому сложность выполнения -м шаге выполняются только вычитания чисел, умножения на степень двойки, а также сравниваются между собой числа. Поэтому сложность выполнения  -го шага можно оценить как -го шага можно оценить как  . Кроме того, из неравенства . Кроме того, из неравенства  , вытекает, что , вытекает, что . .Значит,  . Данная оценка числа шагов LSBGCD-алгоритма позволяет получить общую оценку его сложности в виде . Данная оценка числа шагов LSBGCD-алгоритма позволяет получить общую оценку его сложности в виде  . [8] . [8] |
