многочлены. Курсовая яна. Нод и нок многочленов
 Скачать 96.48 Kb. Скачать 96.48 Kb.
|
2.3 Алгоритм Евклида нахождения наибольшего общего делителя двух чиселПусть даны целые числа 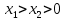 . Для вычисления наибольшего делителя . Для вычисления наибольшего делителя 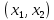 существует хорошо известный алгоритм Евклида. существует хорошо известный алгоритм Евклида.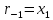 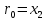 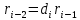 , , 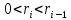 , , 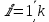 Тогда 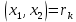 и для его нахождения требуется выполнить и для его нахождения требуется выполнить 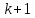 делений с остатком. Оценим сначала количество шагов алгоритма Евклида.[4] делений с остатком. Оценим сначала количество шагов алгоритма Евклида.[4]Определение 3. Последовательностью чисел Фибоначчи называется рекуррентная последовательность вида  Обозначим также через  положительный корень квадратного уравнения положительный корень квадратного уравнения  Лемма 1. При любом  справедливо неравенство справедливо неравенство  . .Доказательство проведем индукцией по  . При . При  неравенство проверяется непосредственно. Далее, используя предположение индукции и определение последовательности Фибоначчи, имеем неравенство проверяется непосредственно. Далее, используя предположение индукции и определение последовательности Фибоначчи, имеем  Теорема 1.3. Число делений с остатком в алгоритме Евклида для нахождения наибольшего общего делителя чисел  не превосходят величины не превосходят величины  Доказательство. Индукцией по  докажем, что докажем, что  . При . При  данное неравенство выполнено, так как данное неравенство выполнено, так как  . Для . Для  в силу предположения индукции имеем в силу предположения индукции имеем . .В силу доказанного  или или  Из последнего неравенства следует оценка числа шагов алгоритма Евклида. Теперь оценим сложность алгоритма Евклида. Пусть  , где , где  - число шагов алгоритма. Очевидно, выполняются условия - число шагов алгоритма. Очевидно, выполняются условия . Тогда, учитывая сложность деления с остатком, можно оценить сложность алгоритма Евклида величиной . Тогда, учитывая сложность деления с остатком, можно оценить сложность алгоритма Евклида величиной  . .Так как  оценивается теоремой 1.3 как оценивается теоремой 1.3 как  , то сложность всего алгоритма можно оценивать величиной , то сложность всего алгоритма можно оценивать величиной  . Если длина чисел . Если длина чисел  не превосходит не превосходит  , то полученная оценка имеет вид , то полученная оценка имеет вид  . .Без доказательства приведем еще одну оценку для количества шагов алгоритма Евклида. [7] Теорема 1.4. Число делений с остатком в алгоритме Евклида для нахождения наибольшего общего делителя  не превосходит величины не превосходит величины  . .Замечание. Оценка теоремы Ламе достижима. Так  , и для нахождения наибольшего общего делителя требуется ровно 5 шагов алгоритма Евклида. , и для нахождения наибольшего общего делителя требуется ровно 5 шагов алгоритма Евклида. Приведем также без доказательства теорему о среднем числе шагов алгоритма Евклида. Теорема 1.5. Если целочисленные случайные величины  равномерно и независимо распределены на множестве равномерно и независимо распределены на множестве  , и , и  - случайная величина, равная числу шагов алгоритма Евклида нахождения - случайная величина, равная числу шагов алгоритма Евклида нахождения  , то , то . .При переходе к десятичным логарифмам имеем  . Значит, полученные выше оценки числа шагов алгоритма Евклида в среднем завышены примерно в два с половиной раза. [4] . Значит, полученные выше оценки числа шагов алгоритма Евклида в среднем завышены примерно в два с половиной раза. [4] |
