многочлены. Курсовая яна. Нод и нок многочленов
 Скачать 96.48 Kb. Скачать 96.48 Kb.
|
2.2 Наименьшее общее кратноеПусть даны многочлены 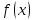 и и 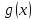 над полем над полем 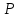 . .Определение 1. Многочлен 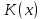 называется общим кратным многочленов называется общим кратным многочленов 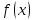 и и 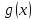 , если , если 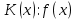 и и 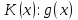 . .Определение 2. Наибольшим общим кратным (НОК) многочленов 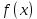 и и 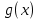 называется такое их общее кратное, на которое делится любое общее кратное этих многочленов. называется такое их общее кратное, на которое делится любое общее кратное этих многочленов.Замечание. Наибольшим общим кратным (НОК) многочленов 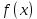 и и 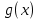 обозначается НОК ( обозначается НОК (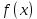 , , 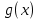 ) или НОК ) или НОК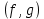 или или 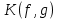 . .Теорема 1. НОК многочленов 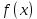 и и 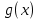 вычисляется по формуле: вычисляется по формуле: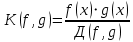 (1.6) (1.6)Таким образом, НОК двух многочленов есть частное от деления произведения этих многочленов на их НОД. Доказательство. Пусть НОД многочленов 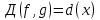 , тогда , тогда 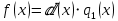 и и 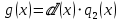 . Поставим в формулу 1.6 вместо . Поставим в формулу 1.6 вместо 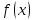 его значение, получим: его значение, получим: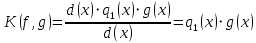 Следовательно, 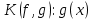 . .В равенстве 1.6 подставим вместо 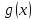 его значение, получим: его значение, получим: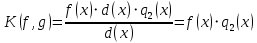 Следовательно, 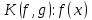 . .Итак, многочлен 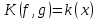 является общим кратным многочленов является общим кратным многочленов 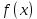 и и 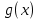 . Пусть . Пусть 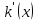 есть наименьшее общее кратное многочленов есть наименьшее общее кратное многочленов 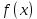 и и 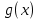 . Требуется доказать, что . Требуется доказать, что 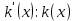 . Так как . Так как 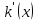 – общее кратное – общее кратное 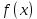 и и 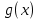 , то , то 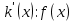 и и 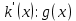 . Пусть . Пусть 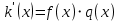 и и 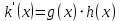 . Будем иметь, что . Будем иметь, что 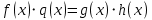 . Делим обе части последнего равенства на . Делим обе части последнего равенства на 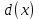 и получаем: и получаем: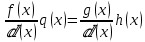 Многочлены 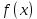 и и 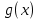 делятся на свой НОД делятся на свой НОД 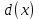 , в частном получим взаимно простые многочлены , в частном получим взаимно простые многочлены 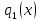 и и 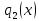 . Многочлен . Многочлен 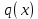 будет делиться на будет делиться на 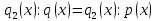 . Подставляя значение . Подставляя значение 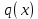 в равенство в равенство 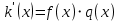 , будем иметь: , будем иметь: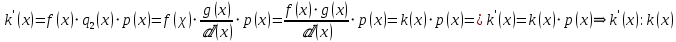 Итак, любое любое общее кратное многочленов 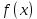 и и 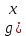 ) делится на ) делится на 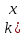 ). Следовательно, ). Следовательно, 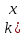 ) есть НОК многочленов ) есть НОК многочленов 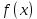 и и 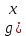 ). Теорема доказана. [1,2,11] ). Теорема доказана. [1,2,11]Пример 1. Найти НОК многочленов. 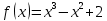 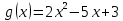 Решение: Найдем НОД 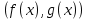 А) 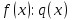 . Получаем, что . Получаем, что 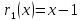 ; ;Б) 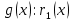 . Получаем, что . Получаем, что 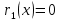 ; ;Итак, НОД 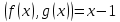 . .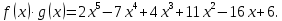 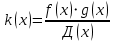 По схеме Горнера 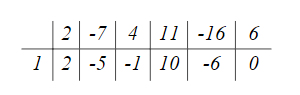 Ответ: 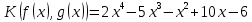 . . |
