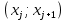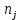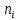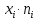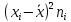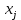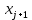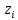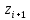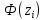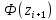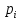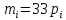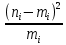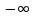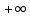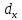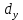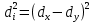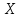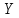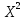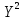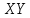Теория вероятностей и мат статистика. Теория вероятностей контрольн. Нормальное распределение 3 Задача Тема Интервальные оценки 3
 Скачать 55.4 Kb. Скачать 55.4 Kb.
|
|
Оглавление Задача 1. Тема: «Нормальное распределение» 3 Задача 2. Тема: «Интервальные оценки» 3 Задача 3. Тема: «Проверка статистических гипотез» 4 Задача 4. Тема: «Критерий согласия Пирсона» 5 Задача 5. Тема: «Ранговая корреляция» 6 Задача 6. Тема: «Линейная корреляция и регрессия» 7 Задача 1. Тема: «Нормальное распределение» Средний срок службы коробки передач до капитального ремонта у автомобиля определенной марки составляет 56 мес. со стандартным отклонением 16 мес. Привлекая покупателей, производитель хочет дать гарантию на этот узел, обещая сделать бесплатно любое число ремонтов коробки передач нового автомобиля в случае ее поломки до определенного срока. Пусть срок службы коробки передач подчиняется нормальному закону. На сколько месяцев в таком случае производитель должен дать гарантию для этой детали, чтобы число бесплатных ремонтов не превышало 2,275% проданных автомобилей? Решение Дано 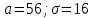 Срок службы должен оказаться в интервале 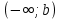 при условии при условии 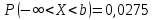 Вероятность попадания величины X в заданный интервал 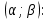 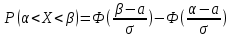 , где Ф – интегральная функция Лапласа , где Ф – интегральная функция ЛапласаИмеем: 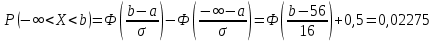 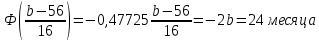 Ответ:число бесплатных ремонтов не превысит 2,275% проданных автомобилей при условии, что производитель даст гарантию на коробку передач на срок 24 месяца. Задача 2. Тема: «Интервальные оценки» С помощью случайной выборки оценивается среднее время ежедневного просмотра телепередач абонентами кабельного телевидения в период с 18 до 22 ч. Каким должен быть объем выборки в этом случае, если в предыдущих выборочных обследованиях стандартное отклонение времени просмотра передач составило 40 мин., а отклонение выборочной средней от генеральной средней по абсолютной величине не должно превышать 5 мин. с вероятностью 0,9? Решение По условию: 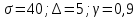 Для определения объема повторной выборки, необходимого для того, чтобы гарантировать определенную точность оценки генеральной средней, задаваемую предельной ошибкой выборки , при заданной надежности , используем формулу: 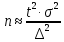 По условию задачи доверительная вероятность равна 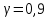 , что соответствует , что соответствует 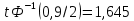 , , Таким образом, объем повторной выборки приблизительно будет равен: 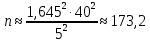 Учитывая, что необходимо не превышать заданную ошибку, округляем результат до большего целого: 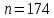 Итак, чтобы с вероятностью 0,9 и точностью 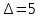 минут оценить среднее время ежедневного просмотра телепередач абонентами кабельного телевидения в период с 18 до 22 час., требуется обследовать не менее 174 абонентов. минут оценить среднее время ежедневного просмотра телепередач абонентами кабельного телевидения в период с 18 до 22 час., требуется обследовать не менее 174 абонентов.Задача 3. Тема: «Проверка статистических гипотез» Компания по производству безалкогольных напитков предполагает выпустить на рынок новую модификацию популярного напитка, в котором сахар заменен сукразитом. Компания хотела бы быть уверенной в том, что не менее 70% ее потребителей предпочтут новую модификацию напитка. Новый напиток был предложен на пробу 2000 человек, и 1422 из них сказали, что он вкуснее старого. Может ли компания отклонить предположение о том, что только 70% всех ее потребителей предпочтут новую модификацию напитка старой? Уровень значимости 0,01. Решение Для решения данной задачи необходимо проверить гипотезу о том, что неизвестная генеральная доля точно равна числовому значению. Сформулируем нулевую и конкурирующую гипотезы согласно условиям задачи. 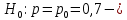 только 70% потребителей предпочтут новую модификацию напитка только 70% потребителей предпочтут новую модификацию напитка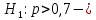 новый напиток предпочтут более 70% потребителей. новый напиток предпочтут более 70% потребителей. Критическая область - правосторонняя Вычислим наблюдаемое значение статистики K по формуле: 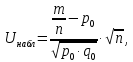 где 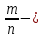 относительная частота появления события; относительная частота появления события;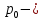 гипотетическая вероятность появления события; гипотетическая вероятность появления события;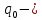 гипотетическая вероятность непоявления события; гипотетическая вероятность непоявления события;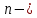 объем выборки. объем выборки.При заданных значениях: 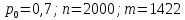 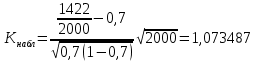 По таблице функции Лапласа найдем критическую точку для правосторонней критической области (при гипотезе 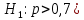 по уровню значимости по уровню значимости 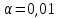 : : 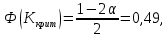 откуда откуда 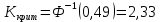 Так как 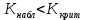 , следовательно, на данном уровне значимости нет оснований отклонять нулевую гипотезу в пользу конкурирующей. По данным проверки с более чем 99%-ной надежностью компания не может отклонить предположение о том, что только 70 процентов всех ее потребителей предпочтут новую модификацию напитка старой. , следовательно, на данном уровне значимости нет оснований отклонять нулевую гипотезу в пользу конкурирующей. По данным проверки с более чем 99%-ной надежностью компания не может отклонить предположение о том, что только 70 процентов всех ее потребителей предпочтут новую модификацию напитка старой.Задача 4. Тема: «Критерий согласия Пирсона» С помощью критерия согласия Пирсона на уровне значимости α = 0,05 выяснить, можно ли считать случайную величину X, заданную в виде сгруппированного статистического ряда, нормально распределенной с параметрами 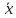 и и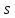 , рассчитанными по выборке. , рассчитанными по выборке.
Решение Для нахождения характеристик выборки от заданного интервального распределения признака X перейдем к дискретному распределению, выбирая в качестве значений признака 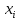 серединычастичных интервалов. Для удобства дальнейших расчетов заполним таблицу: серединычастичных интервалов. Для удобства дальнейших расчетов заполним таблицу:
Выборочная средняя 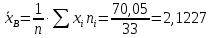 Выборочная исправленная дисперсия:  Выборочное исправленное с.к.о: 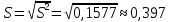 Сформулируем основную и альтернативную гипотезы. 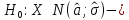 случайная величина X подчиняется нормальному закону с параметрами случайная величина X подчиняется нормальному закону с параметрами  истинные значения параметров не известны, используем их наилучшие оценки, рассчитанные по выборке. истинные значения параметров не известны, используем их наилучшие оценки, рассчитанные по выборке.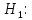 случайная величина X не подчиняется нормальному закону с данными параметрами. случайная величина X не подчиняется нормальному закону с данными параметрами.Используя данные интервального ряда и вычисленные значения 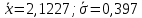 , по формуле , по формуле 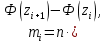 где где 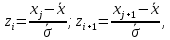 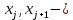 начало и конец начало и конец 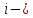 го интервала, го интервала, 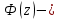 функция Лапласа, найдем слагаемые статистики Пирсона. Начало первого и конец последнего интервалов примем функция Лапласа, найдем слагаемые статистики Пирсона. Начало первого и конец последнего интервалов примем 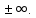
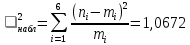 Число степеней свободы: 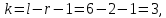 где где 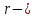 количество параметров, оцененных по выборке количество параметров, оцененных по выборке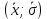 Для уровня значимости 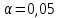 и и 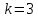 находим критическое значение находим критическое значение 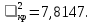 Так Так 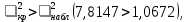 то гипотезу о нормальном распределении Х принимаем. то гипотезу о нормальном распределении Х принимаем.Задача 5. Тема: «Ранговая корреляция». По заданной таблице рангов найти выборочный коэффициент ранговой корреляции Спирмена и проверить значимость полученного результата при α = 0.05. Десять спортсменов-бегунов проранжированы по двум признакам: X — рост спортсмена, Y — скорость бега.
Решение Составим матрицу рангов и найдем сумму квадратов разностей рангов 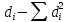
Вычислим значение коэффициента Спирмена по формуле 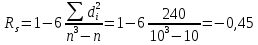 По шкале Чеддока связь между ростом спортсмена и скоростью бега умеренная 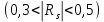 и обратная и обратная 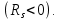 Для проверки значимости найденного значения 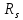 , выдвинем следующие статистические гипотезы: , выдвинем следующие статистические гипотезы: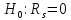 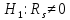 Вычислим наблюдаемое значение статистики: 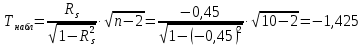 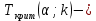 критическая точка двусторонней критической области, которую находим по таблице критических точек распределения Стьюдента по уровню значимости критическая точка двусторонней критической области, которую находим по таблице критических точек распределения Стьюдента по уровню значимости 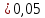 и числу степеней свободы и числу степеней свободы 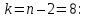 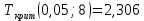 Так как эмпирическое значение коэффициента корреляции Спирмена меньше критического: 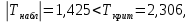 нулевую гипотезу отвергаем: между ростом спортсмена и скоростью бега не существует значимой ранговой корреляционной связи. Коэффициент ранговой корреляции Спирмена статистически незначим. Задача 6. Тема: «Линейная корреляция и регрессия». Исследуется связь между общим весом некоторого растения (Y, %) и весом его семян (X, г) на основе выборочных данных.
Построить диаграмму рассеяния и определить по ней характер зависимости. Рассчитать выборочный коэффициент корреляции Пирсона, проверить его значимость при α = 0.05. Записать уравнение регрессии и дать интерпретацию полученных результатов. Решение Факторный признак Y — общий вес растения; результирующий признак X — вес его семян. Построим диаграмму рассеяния, изобразив в прямоугольной системе координат точки с координатами, соответствующими каждой паре наблюдений 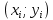 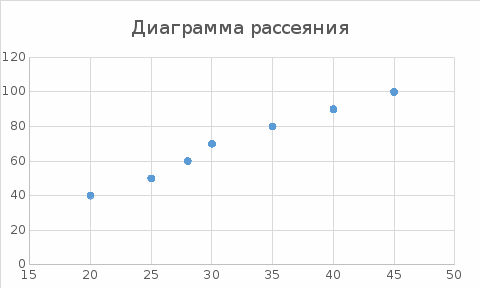 По виду диаграммы можно предположить, что существует линейная корреляционная связь между показателями. Оценим тесноту линейной корреляционной зависимости между признаками и составим выборочные уравнения прямой регрессии. Для удобства проведем все необходимые предварительные расчеты в таблице.
Рассчитаем числовые характеристики выборки, используя итоговую строку расчетной таблицы и учитывая, что объем выборки 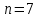 . .Выборочные средние: 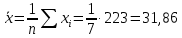 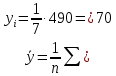 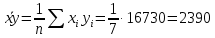 Выборочные дисперсии: 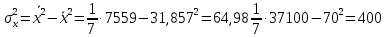 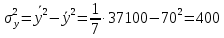 Выборочные среднеквадратические отклонения: 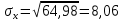 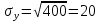 Вычислим выборочный коэффициент корреляции по формуле: 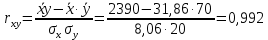 Найдем уравнение линейной регрессии Y на X: 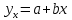 , вычислив параметры уравнения по формулам: , вычислив параметры уравнения по формулам: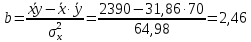 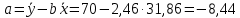 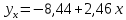 Найдем уравнение линейной регрессии X на Y: 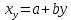 , вычислив параметры уравнения по формулам: , вычислив параметры уравнения по формулам: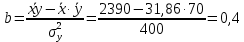 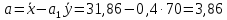 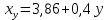 Второй способ. Выборочное уравнение прямой регрессии Y на X и X на Y имеет вид:  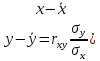 ) ) 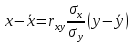 Подставим полученные значения: 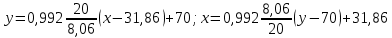 Окончательно получаем, что уравнение прямой регрессии Y на X имеет вид: 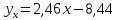 ауравнение прямой регрессии X на Y: 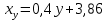 Коэффициент корреляции близок к единице, поэтому прямые регрессии на графике практически совпадают. 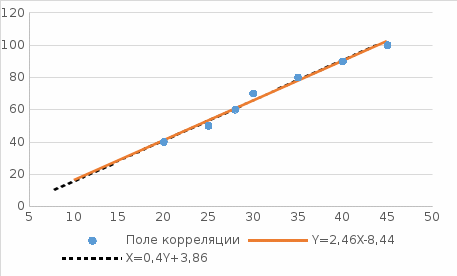 Коэффициент регрессии 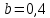 показывает среднее изменение результативного показателя X (вес семян) с повышением или понижением величины фактора Y (общий вес растения). В данном примере с увеличением общего веса растения на 1 %, вес семян повышается в среднем на 0,4 г. Коэффициент показывает среднее изменение результативного показателя X (вес семян) с повышением или понижением величины фактора Y (общий вес растения). В данном примере с увеличением общего веса растения на 1 %, вес семян повышается в среднем на 0,4 г. Коэффициент 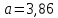 формально показывает прогнозируемый уровень у, но только в том случае, если формально показывает прогнозируемый уровень у, но только в том случае, если 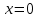 находится близко с выборочными значениями. Можно рассматривать коэффициент находится близко с выборочными значениями. Можно рассматривать коэффициент 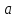 как меру влияния на вес семян других факторов, не включенных в уравнение регрессии. как меру влияния на вес семян других факторов, не включенных в уравнение регрессии.Коэффициент корреляции 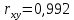 показывает, что зависимость между весом растения и весом семян прямая показывает, что зависимость между весом растения и весом семян прямая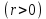 и весьма высокая по шкале Чеддока и весьма высокая по шкале Чеддока 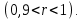 Коэффициент детерминации Коэффициент детерминации 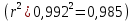 свидетельствует о том, что 98,5% различий в весе семян объясняется общим весом растения, а остальные 1,5% - влиянием других факторов. свидетельствует о том, что 98,5% различий в весе семян объясняется общим весом растения, а остальные 1,5% - влиянием других факторов.Так как регрессивный анализ зависимости между признаками проводится по выборочным данным, необходимо проверить значимость выборочного коэффициента корреляции. Выдвигаем нулевую гипотезу - величина коэффициента корреляции в генеральной совокупности равна нулю: 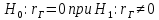 . .Проверку нулевой гипотезы проводим с помощью критерия t – Стьюдента. Наблюдаемое значение критерия t находим по формуле: 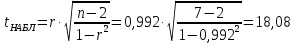 По таблице Стьюдента с уровнем значимости 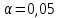 и степенями свободы и степенями свободы 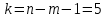 , где , где 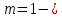 количество объясняющих переменных, находим критическое значение количество объясняющих переменных, находим критическое значение 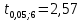 Так как 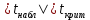 , то полученное значение коэффициента корреляции признается значимым. Нулевая гипотеза отвергается, коэффициент корреляции признается статистически значимым или существенно отличным от нуля в генеральной совокупности. Таким образом, общий вес растения оказывает статистически существенное влияние на вес семян. , то полученное значение коэффициента корреляции признается значимым. Нулевая гипотеза отвергается, коэффициент корреляции признается статистически значимым или существенно отличным от нуля в генеральной совокупности. Таким образом, общий вес растения оказывает статистически существенное влияние на вес семян. |