ДС-131. Лекции 58 и практического занятия 61 по учебной дисциплине Математика (дс131) тверь 2020
 Скачать 114.61 Kb. Скачать 114.61 Kb.
|
|
ВОЕННАЯ АКАДЕМИЯ ВОЗДУШНО-КОСМИЧЕСКОЙ ОБОРОНЫ имени МАРШАЛА СОВЕТСКОГО СОЮЗА Г.К.ЖУКОВА Кафедра основ построения радиоэлектронных средств и систем ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ для курсантов по отработке лекции № 58 и практического занятия № 61 по учебной дисциплине «Математика» (ДС-131) ТВЕРЬ 2020 ЛЕКЦИЯ № 58 ПОСЛЕДОВАТЕЛЬНОСТЬ НЕЗАВИСИМЫХ ИСПЫТАНИЙ, ФОРМУЛЫ ПОЛНОЙ ВЕРОЯТНОСТИ И БАЙЕСА 1. Частная теорема о повторении опытов (схема Бернулли) При практическом применении теории вероятностей часто встречаются задачи, в которых один и тот же опыт повторяется неоднократно. В результате каждого опыта может появиться или нет некоторое событие А, вероятность появления которого в каждом опыте известно. При этом нас интересует вероятность появления события А – конкретное количество раз во всей серии опытов. Примеры. 1. По прикрываемому группировкой ПВО объекту наносят удар 5 самолетов противника, каждый из которых сбивается с вероятностью 0,6. Какова вероятность того, что группировка уничтожит все самолеты; 4 самолета; не более трех самолетов. 2. В составе группировки РТВ 4 РЛС, зоны обнаружения которых перекрываются. Каждая РЛС обнаруживает ведущую цель с вероятностью 0,4. Какова вероятность того, что цель будет обнаружена двумя РЛС. 3. По n целям произведен пуск n БР (по каждой цели одну БР). Вероятность поражения одной цели БР равна Р. Какова вероятность поражения m целей; не менее m целей (m n). 4. Пункт радиоперехвата из-за низкой подготовленности оператора пропускает радиограмму противника с вероятностью 0,3. Какова вероятность пропуска трех радиограмм из 5; не менее двух радиограмм из 6; хотя бы одной радиограммы из 4. 5. Из зенитного орудия произведено пять выстрелов по самолету противника. Вероятность попадания при каждом выстреле 0,3. Какова вероятность попадания в самолет: трех снарядов; не менее четырех снарядов; хотя бы одного снаряда. Примеры подобного типа легко решаются, если опыты независимые, т. е. если вероятность того или иного исхода каждого из опытов не зависит от того, какие исходы имели остальные опыты. Например, несколько выстрелов представляют собой независимые опыты только в том случае, если прицеливание производится заново перед каждым выстрелом; в случае, когда прицеливание производится один раз перед всей стрельбой или непрерывно осуществляется в процессе стрельбы (стрельба очередью, бомбометание серией), выстрелы представляют собой зависимые опыты. В нашем курсе будем рассматривать только независимые опыты. Если независимые опыты производятся в одинаковых условиях, то вероятность события А во всех опытах одна и та же, если же в неодинаковых условиях, то вероятность события А меняется от опыта к опыту. Например, если производится ряд независимых выстрелов в переменных условиях (скажем, при изменяющейся дальности), то вероятность попадания от выстрела к выстрелу может заметно меняться. К первому случаю относится частная теорема о повторении опытов, ко второму – общая теорема о повторении опытов. Частная теорема о повторении опытов отвечает на вопрос : чему равна вероятность Рm,n появления события А ровно m раз в серии из n независимых опытов, если вероятность появления события А в каждом опыте постоянна и равна Р. Проводят n независимых опытов. В каждом опыте может появиться событие А. Р(А) = р. Найти вероятность появления события А ровно m раз в серии из n опытов. Рm,n = ? 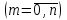 . .Введем событие : Ai – появление события А в i-том опыте; 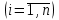 . .Известно Ai – независимые события и Р(Ai) = р. 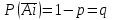 . .Обозначим : В – появление события А ровно m раз в серии из n опытов. Очевидно, 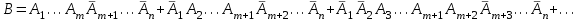 Так как опыты независимы, то вероятность каждого слагаемого по теореме умножения вероятностей равна Так как опыты независимы, то вероятность каждого слагаемого по теореме умножения вероятностей равна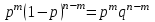 . .Так как все эти варианты несовместны, а их количество равно 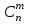 , то по теореме сложения вероятностей , то по теореме сложения вероятностей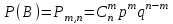 – формула Бернулли (1) – формула Бернулли (1)Формулировка частной теоремы. Если проводится n независимых опытов, в каждом из которых событие А появляется с вероятностью р, то вероятность появления события А ровно m раз, выражается формулой 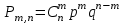 , ,где q = 1 – р. Во многих задачах надо уметь вычислять вероятность появления события А не менее к раз, более к раз, менее к раз, не более к раз в серии из n опытов. В подобных случаях удобно ввести случайную величину Х – число появления события А в серии из n опытов. Тогда , например, вероятность появления события А не менее к раз запишется: 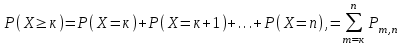 , ,где каждое из слагаемых вычисляется дальше по формуле Бернулли. Пример. По наземной цели производится пуск 6 неуправляемых реактивных снарядов. Вероятность попадания в цель любого снаряда равна 0,4. Какова вероятность того, что в цель попадает а) 2 снаряда; б) менее двух снарядов; в) не менее 4-х снарядов. РЕШЕНИЕ Х – число попавших снарядов а) 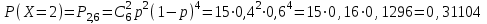 . .б) 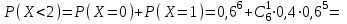 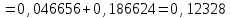 . .в) 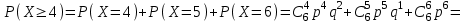 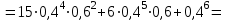 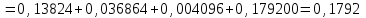 . .2. Расчет вероятности выполнения поставленной задачи, формула наряда боевых средств Широкое применение в оперативно–тактических расчетах находит формула расчета вероятности появления события А хотя бы один раз в серии из n опытов: 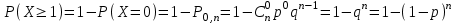 . .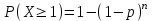 (2) (2)Нетрудно сообразить, что по формуле (2) вычисляется вероятность выполнения поставленной перед n средствами задачи, когда вероятность выполнения задачи каждым средством равна р и задача считается выполненной, если ее выполнит хотя бы одно средство. Пример 3. По прикрываемому группировкой ПВО объекту наносят удар n самолетов противника, каждый из которых может быть сбит с вероятностью Рсб. Прорвавшийся к объекту самолет поражает его с вероятностью Рпор . Объект уничтожается при поражении его хотя бы одним самолетом противника. Найти вероятность уничтожения объекта. р1 – вероятность выполнения задачи любым самолетом, 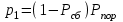 . .Хотя бы один самолет должен выполнить задачу, т.е. 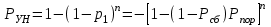 . .Одной из важнейших задач, которую приходится решать при организации боевых действий подразделений, частей и соединений войск, при планировании операции, а также в ходе боевых действий, это задача расчета наряда боевых средств. ЗАДАЧА. Сколько боевых средств n требуется для того, чтобы с вероятностью не менее Рзад поразить одиночную цель, если выстрелы независимые, вероятность поражения цели каждым средством равна р1 , а для поражения цели достаточно поражения ее хотя бы одним средством. Вероятность поражения цели при пуске по ней n средств вычисляется по формуле: 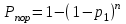 . .По условию задачи должно выполняться : Рпор Рзад . 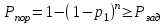 , , 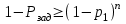 , , 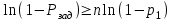 , ,откуда 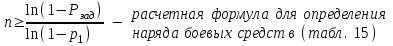 . .Пример 1. Для разрушения подземной стартовой позиции противника выделяется ракетное соединение. Вероятность преодоления ракетной системы ПВО противника равна 0,6. Вероятность поражения стартовой позиции прорвавшейся ракетой равна 0,8. Сколько нужно выделить ракет поражения стартовой позиции с вероятностью не менее 0,9 ? РЕШЕНИЕ По условию задачи полная вероятность поражения позиции одной ракетой : р1 = 0,60,8 = 0,48 ; Рзад = 0,9. Тогда 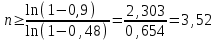 , т.е. n 4. , т.е. n 4.3. Общая теорема о повторении опытов (полиномиальная схема) Общая теорема о повторении опытов отвечает на вопрос : какова вероятность Рm,n того, что событие А появится ровно m раз в серии из n независимых опытов, если вероятность появления события А в i-ом опыте равна 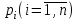 . .Для нахождения вероятности Рm,n используется обычно формальный прием. Составляют производящую функцию 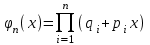 , ,где х – произвольный параметр. Доказано, что раскрыв скобки и приведя подобные члены, получим многочлен n-й степени относительно х вида 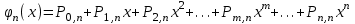 , ,т.е. вероятность Рm,n является коэффициентом при хm (полиномиальная схема). Теорема формулируется так: Вероятность того, что событие А в n независимых опытах появится ровно m раз равна коэффициенту при xm в выражении производящей функции 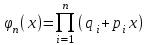 , ,где рi - вероятность появления события А в i-м опыте, qi = 1 – pi, х - произвольный параметр. Пример. Производится три независимых выстрела по одной и той же мишени с различных расстояний. Вероятности попадания при этих выстрелах соответственно равны 0,2; 0,4; 0,6. Найти : а) вероятность 2-х попаданий; б) вероятность поражения мишени, если для этого достаточно не менее одного попадания; в) вероятность не менее двух попаданий. РЕШЕНИЕ. n = 3; р1 = 0,2 ; р2 = 0,4 ; р3 = 0,6. 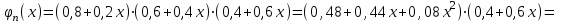 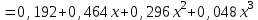 . .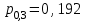 ; ; 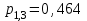 ; ; 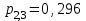 ; ; 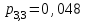 . .4.Формула полной вероятности и формулы Байеса Рассмотрим задачу. Две РЛС ведут наблюдение за целью, которая может применять или не применять помехи. Если цель не применяет помехи, то за один цикл обзора станция обнаруживает ее с вероятностью 0,7, если применяет – с вероятностью 0,2. Вероятность того, что за время цикла будут применены помехи, равна 0,4 и не зависит от того, как и когда применялись помехи в остальных циклах. Определить вероятность обнаружения цели за один цикл обзора РЛС. Задача характерна тем, что интересующее нас событие имеет различную вероятность в зависимости от той ситуации, которая будет иметь место, причем заранее мы не знаем, какая именно ситуация осуществится в результате опыта. Отметим, что до опыта мы можем рассчитать и вероятности различных ситуаций и вероятность интересующего нас события в рамках каждой из этих ситуаций. Решение подобных задач легко поддается формализации введением событий – гипотез. Предварительно введем понятие полной группы событий. События Е1, Е2, …Еn – образуют полную группу попарно–несовместных событий в данном опыте, если в результате опыта обязательно происходит только одно из них. События Е1, Е2, …Еn будем в дальнейшем называть гипотезами. Очевидно, что 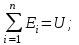 Ei Ej = V при i j Ei Ej = V при i jПостановка задачи Пусть событие А может произойти вместе с одной из гипотез  . .Известны доопытные (априорные) вероятности гипотез P (Ei) и условные вероятности события А при каждой из этих гипотез Р (А / Еi). Тогда полная вероятность события А определяется формулой 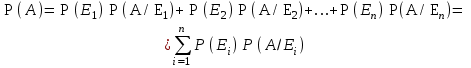 Доказательство: Тот факт, что событие А может произойти вместе с одной из гипотез Еi, можно изобразить следующим образом: 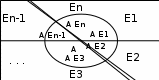 Из рисунка видно, что 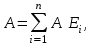 причем, события А Еi – несовместные. причем, события А Еi – несовместные.Тогда 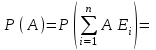 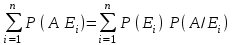 Итак, 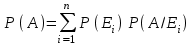 – формула полной вероятности. – формула полной вероятности.Причем, т.к. 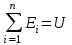 и Еi – несовместны, то и Еi – несовместны, то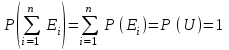 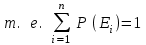 Приведем теперь решение сформулированной ранее задачи. Событие А – обнаружение объекта за один цикл. Введем гипотезы: Е1 – объект применяeт помехи; Е2 – объект не применяет помехи. Очевидно, P (E1) = 0,4; P (E2) = 0,6; Тогда Р (А / Е1) = 1 – (1 – 0,2)2 = 0,36 и Р (А / Е2) = 1 – (1 – 0,7)2 = 0,91 По формуле полной вероятности находим Р (А) = 0,4 0,36 + 0,6 0,91 = 0,69. Рассмотрим теперь формулы Байеса. Постановка задачи. Пусть до опыта было известно, что событие А может произойти вместе с одной из гипотез Е1, Е2, …Еn. Известны доопытные (априорные) вероятности гипотез P (Ei)  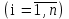 и условные вероятности события А при каждой из этих гипотез Р (А / Еi), и условные вероятности события А при каждой из этих гипотез Р (А / Еi), 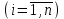 . Произведен опыт и стало известно, что событие А произошло. Это вызывает переоценку вероятностей гипотез и задача состоит в том, чтобы по имеющейся информации об исходе опыта найти новые (послеопытные или апостериорные) вероятности Р (Еi / А) этих гипотез. . Произведен опыт и стало известно, что событие А произошло. Это вызывает переоценку вероятностей гипотез и задача состоит в том, чтобы по имеющейся информации об исходе опыта найти новые (послеопытные или апостериорные) вероятности Р (Еi / А) этих гипотез.Естественно ожидать, что результат опыта может изменить наши сведения о вероятностях гипотез в зависимости от того, произошло или нет событие А в результате опыта. Следовательно, можно после опыта попытаться определить новые вероятности гипотез, отличные от тех, которыми они характеризовались до опыта. Количественная переоценка вероятностей гипотез производится с помощью формул, получивших название формул Байеса (другое название – теорема гипотез). Послеопытные (апостериорные) вероятности гипотез Р (Еi / А) определяются соотношением 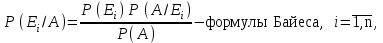 где Р (А) – вычисляется по формуле полной вероятности. Действительно, используя теорему умножения вероятностей для каждой гипотезы Еi, можно записать P (A Ei) = P (A) P (Ei / A) или P (A Ei) = P (Ei) P (A / Ei) откуда: Р (А) Р (Ei / A) = Р (Еi) P (A / Ei). Из последнего равенства, разрешая его относительно P (Ei / A), считая, что Р (А) 0, получаем 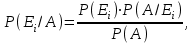 что и требовалось доказать. Итак, формулы Байеса позволяют произвести переоценку вероятностей гипотез на основе информации об исходе опыта. При этом 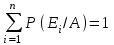 . .Пример. Вероятность наличия цели в зоне обзора РЛС равна 0,4. Вероятность обнаружения отраженного от цели радиолокационного сигнала на фоне помех равна 0,6. Вероятность появления ложного сигнала на индикаторе на счет помех при отсутствии цели равна 0,02. Какова вероятность того, что появление сигнала на экране индикатора вызвано появлением цели, а не случайным действием помехи. Решение А – появление сигнала на экране индикатора. Гипотезы: Е1 – наличие цели в зоне наблюдения радиолокатора; Е2 – отсутствие цели в зоне наблюдения радиолокатора. Требуется найти Р (Е1 / А). Р (Е1) = 0,4 Р (А / Е1) = 0,6 Р (Е2) = 0,6 Р (А / Е2) = 0,02 Р(А)=0,4 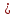 0,6+0,6 0,6+0,6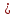 0,02=0,252 0,02=0,252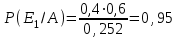 т.е. в 95% случаев можно считать, что появление отметки на экране индикатора говорит о наличии цели. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №62 РЕШЕНИЕ ЗАДАЧ НА ТЕОРЕМЫ О ПОВТОРЕНИИ ОПЫТОВ Вычисление вероятностей событий по схеме Бернулли. Задача 1(№ 64). Пяти РЛС поставлена задача по обслуживанию цели. Вероятность обнаружения цели каждой РЛС равна 0,6. Какова вероятность того, что цель обнаружат: а) три РЛС; б) более трех РЛС; в) не менее двух РЛС; г) не более четырех РЛС; д) хотя бы одна РЛС. Задача 2 (№ 73). Для огневого подавления трех РЛС противник назначил по два самолета на каждую РЛС. Вероятность обнаружения станции парой самолетов равна 0,8. Вероятность поражения обнаруженной РЛС одним самолетом равна 0,6. Определить вероятность того, что а) будут поражены две РСЛ; б) будет поражена хотя бы одна РЛС; в) будет поражено не менее двух РЛС. Задача 3 (№ 82). Сколько истребителей должно атаковать цель, чтобы поразить ее с вероятностью не менее 0,9, если каждый истребитель пускает независимо две ракеты с вероятностью поражения каждой 0,3. Задача 4 (№ 71). Для завязки траектории движения цели ее необходимо обнаружить не менее 2-х раз за три обзора РЛС. Вероятность обнаружения в каждом обзоре различна и равна в первом обзоре – 0,5; во втором – 0,6; в третьем – 0,7. Обнаружения в каждом обзоре независимы. Найти вероятность завязки траектории. Задача 5 Имеется три рубежа ПВО. Вероятность сбить цель на первом рубеже равна 0,3; на втором – 0,4; на третьем 0,2. На объект противник направил три цели. Определить вероятность того, что а) только одна цель пройдет ко второму рубежу; б) на каждом рубеже будет сбито по одной цели; в) объект будет поражен, если любая прорвавшаяся к объекту цель поражает его с вероятностью 0,7. Задача 6 Два стрелка производят по три выстрела каждый по своей мишени. При любом выстреле первый стрелок попадает в мишень с вероятностью 0,6, второй – с вероятностью 0,7. Найти вероятность того, что а) один из стрелков попадет один раз, а другой – два раза.; б) у обоих стрелков будет одинаковое число попаданий; в) у первого стрелка будет больше попаданий, чем у второго. 2. Расчет наряда боевых средств Задача 7 Вероятность поражения цели одной ракетой равна 0,4. Сколько ракет надо пустить по цели, чтобы поразить ее с вероятностью не менее 0,95. Задача 8 Сколько истребителей должно атаковать цель, чтобы поразить ее с вероятностью не менее 0,9, если каждый истребитель пускает независимо две ракеты с вероятностью поражения каждой 0,3. Вычисление вероятностей событий по общей теореме о повторении опытов Задача 9 Для завязки трассы цели ее необходимо обнаружить не менее двух раз за три обзора РЛС . Вероятность обнаружения цели в первом обзоре 0,5; во втором – 0,6: в третьем -0,7. Обнаружения в обзорах независимы. Определить вероятность завязки трассы. Задача 10 По позиции дивизиона противник с разных дальностей запускает три крылатых ракеты. Вероятности попадания их на позиции дивизиона соответственно равны р1 = 0,4; р2 = 0,5; р3 = 0,6. Определить вероятности попадания а) одной крылатой ракеты; б) двух крылатых ракет; в) трех крылатых ракет; г) не менее двух крылатых ракет; д) не более одной крылатой ракеты; е) ни одной крылатой ракеты. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №63 РЕШЕНИЕ ЗАДАЧ НА ФОРМУЛЫ ПОЛНОЙ ВЕРОЯТНОСТИ И БАЙЕСА Вычисление полных вероятностей событийЗадача № 1. Вероятность того, что во время работы ЭВМ возникает сбой в АУ (арифметическое устройство), ОП (оперативная память) и остальных устройствах, относятся как 3: 2: 5. Вероятности обнаружения сбоя за установленное время в АУ, ОП и остальных устройствах соответственно равны 0,8; 0,9; 0,9. Найти вероятность обнаружения возникшего в машине сбоя. Задача № 2. Два самолета летят бомбить объект. До сбрасывания бомб каждый из них может быть сбит ПВО объекта с вероятностью 0,6. Один прорвавшийся самолет поражает объект с вероятностью 0,5, два с вероятностью 0,7. Найти вероятность сохранения объекта. Задача № 3. Истребителю-перехватчику, вооруженному двумя ракетами, поставлена задача уничтожить цель, которая с вероятностью 0,6 может применять помехи. Вероятность сбития цели одной ракетой равна 0,7, если цель не применяет помехи, и равна 0,4, если цель применяет помехи. Определить полную вероятность уничтожения цели перехватчиком. Задача № 4. На индикатор РЛС от приемного устройства поступает либо сигнал от цели с помехой, либо одна помеха. Вероятность наличия цели в зоне наблюдения РЛС равна 0,6. По наблюдаемой на экране индикатора отметке оператор может с вероятностью 0,4 принять решение о наличии цели при ее отсутствии, и с вероятностью 0,2 принять решение об отсутствии цели при ее наличии. Определить вероятность неверного решения оператора. Задача № 5. На объект противник назначил три самолета. Объектовая группировка ЗРВ может сбить любой самолет с вероятностью 0,6. При прорыве двух самолетов объект поражается с вероятностью 0,5, при прорыве трех самолетов - с вероятностью 0,7, при прорыве одного самолета ущерба объекту не наносится. Определить вероятность сохранения объекта. Задача № 6 В батарее 15 отличных, 20 хороших, 10 удовлетворительных и 5 неудовлетворительных стрелков. Вероятности попадания в мишень при одном выстреле для отличного, хорошего, удовлетворительного и неудовлетворительного стрелков равны соответственно 1; 0,9; 0,7 и 0,4. Для стрельбы наугад вызывается один стрелок и он делает два выстрела по мишени. Какова вероятность того, что в мишени будет ровно одно попадание. Вычисление вероятностей событий по формуле БайесаЗадача 7. В задаче 2 найти вероятность того сбит был один самолет при условии, что объект сохранить не удалось. Задача 8. В задаче 4 найти вероятность поступления сигнала от цели с помехой, при условии неверного решения оператора. Задача 9. В задаче 5 найти вероятность того, что прорвалось три самолета, при условии, что объект был сохранен. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №64 РЕШЕНИЕ ЗАДАЧ НА ВЕРОЯТНОСТНЫЕ РАСЧЕТЫ РАЗЛИЧНЫХ ТИПОВ 1.Выбор вероятностной схемы, расчёт вероятностей событий Задача 1. Бомбардировщик, вооруженный двумя ракетами, обстреливается двумя ракетными установками, каждая из которых поражает его с вероятностью 0,6. Если бомбардировщик не поражен, он обстреливает каждую установку одной ракетой и поражает ее с вероятностью 0,7. Найти вероятность того, что: а) обе установки не будут поражены; б) поражена будет только одна установка; с) хотя бы одна установка будет поражена. Задача 2. Самолет по которому ведется стрельба снарядами, состоит из двух уязвимых частей. Для поражения самолета достаточно двух попаданий в первую часть или трех попаданий во вторую. Первая часть занимает 40% всей площади, вторая – 60%. Определить вероятность поражения самолета, если известно, что в самолет попало три снаряда. Задача 3. Определить наряд ракет для поражения цели с вероятностью не менее 0,85, если вероятность обнаружения цели 0,9, а вероятность поражения обнаруженной цели любым снарядом равна 0,4. Задача 4. Бомбардировщик высылается на бомбометание малоразмерного объекта. Для борьбы со средствами ПВО противника, обороняющими объект, он применяет радиопомехи, которые с вероятностью 0,4 забивают радиолокационные средства ПВО. Если радиолокационные средства противника забиты помехами, то бомбардировщик, не подвергаясь обстрелу, проходит к объекту сбрасывает по нему бомбы и поражает с вероятностью 0,8. Если радиолокационные средства не забиты помехами, то бомбардировщик подвергается обстрелу и может быть сбит с вероятностью 0,7. Определить вероятность поражения объекта. Задача 5. Самолет данного типа осуществляет бомбометание в 45% случаев с высоты h1; в 30% случаев с высоты h2; и в 25% случаев с высоты h3. Вероятности поражения цели при сбрасывании любой бомбы с высот h1, h2, h3 соответственно равны 0,2, 0,3, 0,4. Определить ожидаемую вероятность поражения цели при сбрасывании по цели трех бомб с одной высоты, если для поражения цели достаточно одного попадания. Задача 6. Производится бомбометание по четырем складам боеприпасов одной бомбой. Вероятности попадания в склады соответственно равны 0,15; 0,1; 0,2; 0,25. При попадании в один склад взрываются все четыре. Определить вероятность того, что склады не будут уничтожены. Задача 7. Cамолет, снабженный источником радиопомех, направлен на боевое задание через зону ПВО противника. В зоне ПВО с вероятностью 0,2 против него могут поднять два истребителя, с вероятностью 0,3 – один истребитель и с вероятностью 0,5 против него не будут поднимать истребителей. Каждый поднятый истребитель может с вероятностью 0,4 не выполнять атаку из-за наличия помех. Если же атака состоится, то истребитель с вероятностью 0,8 может сбить самолет. По радио получено сообщение, что самолет прошел зону ПВО. Какова вероятность того, что против него не поднимали истребителей. Задача 8. На пункте радиоперехвата два оператора работают независимо друг от друга. Вероятность радиоперехвата радиограммы первым оператором равна 0,8, вторым – 0,7.Противник передал три радиограммы. Какова вероятность того, что второй оператор перехватит больше радиограмм, чем первый? Задача 9. ПВО объекта состоит из двух рубежей уничтожения. Для удара по объекту противник назначил один стратегический бомбардировщик (СБ), который в случае прорыва через первый рубеж ПВО, не входя во второй, осуществляет пуск двух КР по объекту. На первом рубеже СБ средствами ПВО может быть сбит с вероятностью 0,6. По КР действуют ЗРВ, обстреливая каждую КР двумя ракетами, вероятность поражения КР каждой ракетой равна 0,7. Каждая из КР в случае прохода к объекту поражает его с вероятностью 0,8. Оценить эффективность системы ПВО объекта в данных условиях. Задача 10. Два стрелка делают по одному выстрелу по мишени, состоящей из «яблочка», первого и второго кольца. Каждый из стрелков попадает в «яблочко», первое кольцо, второе кольцо с вероятностями соответственно 0,2, 0,3 и 0,4. За попадание в «яблочко» стрелок получает 5 баллов, в первое кольцо – 3 балла, во второе кольцо – 2 балла. Найти вероятность того, что: а) оба стрелка вместе не получат ни одного бала; б) один из стрелков не получит ни одного балла, а другой не менее трех баллов; в) оба стрелка вместе получат не менее 6 баллов. Задача 11. Команда состоит из двух отличных, двух хороших и четырех посредственных стрелков. Вероятность попадания в мишень при одном выстреле для отличного стрелка равна 0,9, для хорошего – 0,7, для посредственного – 0,4. Наугад вызываются два стрелка и каждый из них производит один выстрел по общей мишени. Какова вероятность того, что: а) в мишень попадет только один из них; б) вызваны были один хороший и один посредственный стрелки, если в мишени оказалось два попадания. Задача 12. Прибор состоит из двух узлов. Работа каждого узла необходима для работы прибора в целом. Вероятность безотказной работы в течение времени 𝛕 первого узла равна р1, второго – р2. Прибор испытывался в течение времени 𝛕, в результате чего он вышел из строя. Какова вероятность того, что отказал только первый узел? |
