Главная страница
Навигация по странице:

  • Ответ

  • 3. Тема: «Проверка статистических гипотез» Вариант 3

  • Задача 4. Тема: «Критерий согласия Пирсона».

  • Задача 5. Тема: «Ранговая корреляция».

  • Задача 6. Тема: «Линейная корреляция и регрессия».

    		•

    теория вероятностей и мат. статистика. Нормальное распределение


    Скачать 306.1 Kb.
    НазваниеНормальное распределение
    Дата15.07.2022
    Размер306.1 Kb.
    Формат файлаdocx
    Имя файлатеория вероятностей и мат. статистика.docx
    ТипКонтрольная работа
    #631352

    Контрольная работа №2

    Вариант 3

    Задача 1. Тема: «Нормальное распределение».

    Вариант 3

    Вес тропического грейпфрута, выращенного в Краснодарском крае, нормально распределенная случайная величина с неизвестным математическим ожиданием и дисперсией, равной 0.04. Агрономы знают, что 65% фруктов весят меньше, чем 0.5 кг. Найдите ожидаемый вес случайно выбранного грейпфрута.

    Решение

    Ожидаемый вес случайно выбранного грейпфрута - это есть математическое ожидание, найти которое можно из формулы попадания нормально распределенной случайной величины в интервал .



    По условию задачи

    А также известно, что





    поэтому



    По таблице Лапласа можно найти, что

    Отсюда получаем 0,5-a=0,077, а=0,5-0,077=0,423.

    Ответ: ожидаемый вес случайно выбранного грейпфрута равен 0,423г.

    Задача 2. Тема: «Интервальные оценки».

    Вариант 3

    Для изучения различных демографических характеристик населения выборочно обследовалось 300 семей города. Оказалось, что среди обследованных семей 15% состоят из двух человек. В каких пределах находится в генеральной совокупности доля семей, состоящих из двух человек, если принять доверительную вероятность равной 0.95?

    Решение.

    В данной задаче требуется построить доверительный интервал для генеральной доли. Определим выборочную долю р.

    Из 300 семей 15% состоит из 2-х человек

    семей состоит из 2-х человек.

    Значит, выборочная доля таких семей составляет



    Поскольку объем выборки n=300>30, найдем из таблиц Лапласа с учетом доверительной вероятности :





    Предельная ошибка выборки равна



    Таким образом, доверительный интервал для генеральной доли по выборочным данным равна

    (0,15-0,04;0,15+0,04) или (0,11; 0,19)

    Доля семей, состоящая из 2-х человек, с вероятностью 0,95 находится в пределах от 11% до 19%.

    Задача 3. Тема: «Проверка статистических гипотез»

    Вариант 3

    Поступление страховых полисов в 130 филиалах страховых компаний в регионе А составило е., в регионе В на 100 филиалов пришлось у.е. Дисперсия величины страховых взносов в регионе А равна , в регионе В — (у.е.) . На уровне значимости α = 0.05 определите, существенно ли различается средняя величина поступления страховых взносов в регионах А и В из расчета на один филиал.

    Решение

    По условию нам известны следующие данные

    Для региона А:

    Для региона B:

    Для того чтобы при заданном уровне значимости проверить нулевую гипотезу

    о равенстве математических ожиданий двух нормально распределенных совокупностей, надо выявить наблюдаемое значение критерия



    По табличной функции Лапласа найдем критическую точку из равенства

    Ф(

    Если | - нет оснований отвергнуть нулевую гипотезу.

    Если | - отвергают нулевую гипотезу

    Вычислим

    Для этого сначала определим .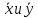





    Тогда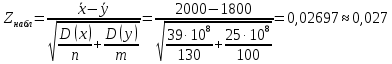

    Из равенства Ф( =

    Используя таблицу Лапласа определим критическую точку :



    0,027<1,96 |

    Значит, нет оснований отвергать гипотезу о равенстве математических ожиданий данных распределений.

    Гипотезу принимаем.

    Значит, различие средних величин поступления страховых взносов в регионах А и В из расчета на 1 филиал не существенны.

    Задача 4. Тема: «Критерий согласия Пирсона».

    С помощью критерия согласия Пирсона на уровне значимости α = 0,05 выяснить, можно ли считать случайную величину X, заданную в виде сгруппированного статистического ряда, нормально распределенной с параметрами x  и s, рассчитанными по выборке.

    Вариант 3
    [2.3;2.5]
    [2.5;2.7]
    [2.7;2.9]
    [2.9;3.1]
    [3.1;3.3]
    [3.3;3.5]



    3
    6
    9
    8
    5
    2

    Для каждого из интервалов определим середину. Имеем

    группы
    середина интервала
    nj
    xj*nj
    x-x ̅
    (x-x ̅)^2)
    ((x-x ̅)^2)*nj

    2.3-2.5
    2,4
    3
    7,2
    -0,47
    0,22
    0,67

    2.5-2.7
    2,6
    6
    15,6
    -0,27
    0,07
    0,45

    2.7-2.9
    2,8
    9
    25,2
    -0,07
    0,01
    0,05

    2.9-3.1
    3
    8
    24
    0,13
    0,02
    0,13

    3.1-3.3
    3,2
    5
    16
    0,33
    0,11
    0,54

    3.3-3.5
    3,4
    2
    6,8
    0,53
    0,28
    0,56

    итого
     
     
    94,8
    0,16
    0,70
    2,39

    =

    Вычислим дисперсию





    Нулевую гипотезу сформулируем как утверждение, что случайная величина Х имеет нормальное распределение с указанными выше параметрами .

    Вычислим теоретические частоты, учитывая n=33,
    , h=0,2



    группы
    Ui
    φ(ui)
    ni

    2.3-2.5
    -1,76
    0,0863
    2,12

    2.5-2.7
    -1,01
    0,242
    5,94

    2.7-2.9
    -0,27
    0,3857
    9,47

    2.9-3.1
    0,47
    0,3565
    8,75

    3.1-3.3
    1,22
    0,1872
    4,59

    3.3-3.5
    1,96
    0,0573
    1,41

    итого
    0,61
    1,315
    32,27

    Сравним эмпирические и теоретические частоты. Составим расчетную таблицу, из которой найдем наблюдаемое значение критерия.








    3
    2.1
    0.9
    0.81
    0.39

    6
    5.9
    0.1
    0.01
    0.002

    9
    9.5
    0.5
    0.25
    0.03

    8
    8.7
    0.7
    0.49
    0.06

    5
    4.6
    0.4
    0.16
    0.03

    2
    1.4
    0.6
    0.36
    0.26



    По таблице критических точек распределения 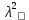по уровню значимости и числу степеней свободы к=6-1-2=3 находим критическую точку правосторонней критической области



    Так как то гипотеза о нормальном распределении генеральной совокупности не отклоняется. Случайная величина Х имеет нормальное распределение с указанными параметрами.

    Задача 5. Тема: «Ранговая корреляция».

    По заданной таблице рангов найти выборочный коэффициент ранговой корреляции Спирмена и проверить значимость полученного результата при α = 0.05.

    Вариант 3. На конкурсе красоты 12 участниц проранжированы по двум признакам: X — артистизм, Y — красота.

    Ранг 1
    11
    4
    10
    1
    8
    9
    2
    12
    6
    7
    5

    Ранг2
    11
    1
    12
    6
    2
    10
    5
    9
    7
    8
    3



    x
    y
    dx
    dy
    (dx-dy)^2

    3
    4
    3
    4
    1

    11
    11
    11
    11
    0

    4
    1
    4
    1
    9

    10
    12
    10
    12
    4

    1
    6
    1
    6
    25

    8
    2
    8
    2
    36

    9
    10
    9
    10
    1

    2
    5
    2
    5
    9

    12
    9
    12
    9
    9

    6
    7
    6
    7
    1

    7
    8
    7
    8
    1

    5
    3
    5
    3
    4

    100



    Связь между признаком X и Y сильная и прямая.

    Значимость коэффициента ранговой корреляции Спирмена

    =2,7

    По таблице Стьюдента



    Поскольку то принимаем гмипотезу о равентсве коэффициента корреляции, т.е. коэффициент ранговой корреляции Спирмена статистически значим

    Задача 6. Тема: «Линейная корреляция и регрессия».

    Для приведенных исходных данных постройте диаграмму рассеяния и определите по ней характер зависимости. Рассчитайте выборочный коэффициент корреляции Пирсона, проверьте его значимость при α = 0.05. Запишите уравнение регрессии и дайте интерпретацию полученных результатов.

    Вариант 3

    Компанию по прокату автомобилей интересует зависимость между пробегом автомобиля (X) и стоимостью ежемесячного технического обслуживания (Y). Для выяснения характера этой зависимости было отобрано 15 автомобилей.

    X
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20

    Y
    3
    16
    15
    20
    19
    21
    26
    24
    30
    32
    30
    35
    34
    40
    39

    РЕШЕНИЕ:

    Построим график исходных данных



    По графику видно, что зависимость прямая, линейная.

    Выборочный коэффициент линейной корреляции Пирсона найдем по формуле:





    Введем нулевую гипотезу H0 :r =0 . Проверим эту гипотезу об отсутствии корреляционной зависимости (о незначимости коэффициента корреляции). Вычислим значение критерия

    Найдем критическую точку по уровню значимости α = 0,05 и числу степеней свободы k =n − 2 =13, получаем tкр. = 2,16. Так как , , следует отвергнуть нулевую гипотезу H0 :r 0 = , то есть корреляционная зависимость есть (существенна), коэффициент корреляции статистически значим.

    Уравнение регрессии Y на X имеет вид . Найдем средние квадратические отклонения.





    Таким образом, наблюдается очень тесная прямая связь между величиной пробега автомобиля и стоимостью ежемесячного технического обслуживания, которая выражается уравнением регрессии . Через каждый год пробега стоимость обслуживания возрастает в среднем на 1,93.

    написать администратору сайта