О. В. Гальцева (Ученая степень, ученое звание, должность) (Ф. И. О.)
 Скачать 448.01 Kb.
|
|
Министерство образования и науки Российской Федерации федеральное государственное автономное образовательное учреждение высшего образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Институт __________ИНК___________________________________________________ Направление подготовки (специальность) __Приборостроение___________________ Кафедра _________ФМПК__________________________________________________ ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к курсовой работе по дисциплине __ Математическое моделирование в приборных системах_____________ на тему _____Математическое моделирование системы автоматического регулирования температуры поливной воды в теплице Выполнил студент гр.__1БМ53________ ____________ __ Е. А. Бугаев _ (Номер группы) (Подпись) (Ф.И.О.) Дата сдачи пояснительной записки преподавателю _____ _____________ 20__г. Руководитель __к.т.н., доцент кафедры ФМПК _ О.В. Гальцева ___ (Ученая степень, ученое звание, должность) (Ф.И.О.) _____________________ ________________________________ (Оценка руководителя) (Подпись) _____ _____________ 20__г. (Дата проверки) Курсовую работу студент __ ______________________выполнил и защитил (Ф.И.О.) с оценкой ______________. Члены комиссии: ________________________ ________________________ ________________________ _____ _____________ 20__г. (дата защиты ) Томск 2015 г. Министерство образования и науки Российской Федерации федеральное государственное автономное образовательное учреждение высшего образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Институт __________ИНК___________________________________________________ Направление подготовки (специальность) __Приборостроение___________________ Кафедра _________ФМПК__________________________________________________ УТВЕРЖДАЮ: Зав. кафедрой А. П. Суржиков (Подпись) (Ф.И.О.) _______ _____________ 20__г. (Дата) ЗАДАНИЕ на выполнение курсовой работы Студенту гр. 1БМ52___ ________________________________ _______________ (ФИО полностью) Тема курсовой работы: Математическое моделирование системы автоматического регулирования температуры поливной воды в теплице Срок сдачи студентом выполненной работы: _ _____2015 г. Исходные данные к курсовой работе: Коэффициенты элементов САР
Содержание пояснительной записки (перечень подлежащих разработке вопросов, в том числе индивидуальное задание): характеристика объекта управления, описание устройства системы автоматического регулирования (САР), описание структурной схемы, принцип работы САР, принципиальная и функциональная схема системы, анализ математической модели САР, анализ выходной характеристики, анализ ЛАЧХ и ЛФЧХ, анализ диаграммы Найквиста, анализ нулей и полюсов системы. Перечень графического материала (с точным указанием обязательных чертежей) Принципиальная схема САР температуры поливной воды в теплице Функциональная схема САР температуры поливной воды в теплице Структурная схема САР температуры поливной воды в теплице Математическая модель САР температуры поливной воды в теплице Выходная характеристика САР температуры поливной воды в теплице ЛАЧХ и ЛФЧХ САР температуры поливной воды в теплице Годограф Найквиста САР температуры поливной воды в теплице Нули и полюса системы САР температуры поливной воды в теплице Дата выдачи задания на выполнение курсовой работы по линейному графику 24 сентября 2015 г. Задание выдал: Руководитель _________________ __________ ___________ ____ _____________ 20__ г. (Степень, звание, должность) (Подпись) (Ф.И.О.) (Дата) Задание принял: Студент гр. ________ ____________ _____________ _____ ___________________ 20___ г. (Подпись) (Ф.И.О.) (Дата) Содержание
Введение В настоящее время проблема автоматического регулирования в различных сферах человеческой деятельности является весьма актуальной. В частности, данные системы используются в области сельского хозяйства. Одним из примеров такого использования является САР температуры поливной воды в теплице. Такие системы предпочтительны как для крупных предприятий, занимающихся выращиванием своей продукции в больших теплицах, так и для обычных сельских жителей, которые имеют в своем распоряжении дачный участок, на котором находятся несколько теплиц. Данная система позволит экономить человеческие ресурсы и время. Целью данной работы является математическое моделирование системы автоматического регулирования температуры поливной воды в теплице и проверка ее на устойчивость. Объектом управления (ОУ) рассматриваемой САР является скоростной водонагреватель. 1 Описание САР температуры поливной воды в теплице 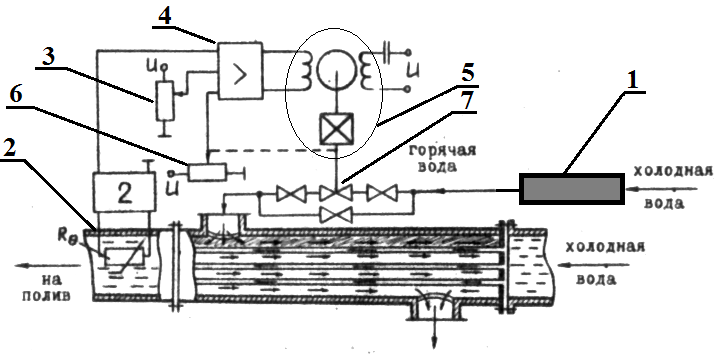 Рис. 1. Функциональная схема САР температуры воздуха в теплице. 1 – Объект управления (скоростной водонагреватель); 2 – Датчик; 3 – Задатчик; 4 – Дифференциальный усилитель; 5 – Исполнительное устройство (электродвигатель и редуктор); 6 – Устройство местной обратной связи; 7 – Регулирующий орган(вентиль). Объектом управления(1) (ОУ) рассматриваемой САР является скоростной водонагреватель. Регулируемой величиной является температура поливной воды. Целью управления является постоянное поддержание температуры поливной воды на заданном уровне. Управляющим воздействием на ОУ является расход горячей воды, протекающей через скоростной водонагреватель. Основное возмущающее воздействие – колебание расхода поливной воды, изменение температуры холодной воды, поступающей из котельной. Датчиком(2) (Д) является термометр сопротивления совместно с измерительным блоком. Входной сигнал для датчика – температура поливной воды, выходной сигнал – величина напряжения Uд. Задатчиком(3) является сопротивление R1. Задающий сигнал – это величина сопротивления R1, которое в определенном масштабе соответствует заданному значению температуры в помещении. Дифференциальный усилитель(4) (ДУ) выполняет функции устройства сравнения (вычитания) входных сигналов и усиления их разности. На вход усилителя поступают напряжения Uд, Uз и напряжение Uос устройства местной обратной связи. Выходной сигнал усилителя - Напряжение Uу, подаваемое на электродвигатель. Исполнительное устройство(5) представляет собой исполнительный механизм, который состоит из электродвигателя и редуктора. Входной сигнал для электродвигателя – напряжение Uу, выходной сигнал – угол поворота φд вала электродвигателя. Входной сигнал для редуктора - φд, выходной сигнал - угол поворота вала φр редуктора. Устройство местной обратной связи(6) (УОС) выполнено в виде потенциометрического датчика перемещения, подвижный контакт которого механически связан с выходным валом редуктора. Входной сигнал УОС – угол поворота φр, выходной сигнал – напряжениеUос. Регулирующим органом(7) (РО) является регулирующий вентиль для жидкостей. Входной сигнал – угол поворота φр, выходной сигнал – расход жидкости через вентиль Qв. 2 Составление и анализ структурной схемы На основании вышеизложенного функциональная схема системы составлена следующим образом: 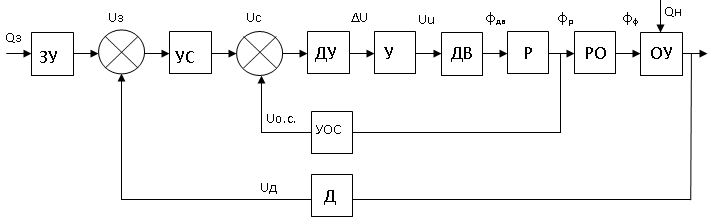 Рис. 2. Структурная схема САР температуры воздуха в теплице Система работает следующим образом: В установившемся режиме при равенстве температуры в водонагревателе заданной выходное напряжение дифференциального усилителя равно 0. При отклонении температуры в водонагревателе от заданной, например, вследствие изменения расхода воды, сопротивление датчика изменяется, и через измерительный блок меняет напряжение на входе в дифференциальный усилитель. Напряжение Uy, являющееся сигналом возникшей ошибки системы, усиливается усилителем и подается на электродвигатель. Двигатель через редуктор открывает заслонку в нужную сторону, тем самым изменяя расход воды, проходящей через водонагреватель. Если температура воды ниже заданной, то угол поворота заслонки увеличивается, если температура выше заданной, то угол поворота заслонки уменьшается. Одновременно выходной вал редуктора перемещает подвижный контакт потенциометрического датчика местной обратной связи, выходное напряжение Uос которого подается на дифференциальный усилитель. Усилитель усиливает разность напряжений Uд, Uз и Uос. За счет местной обратной связи обеспечивается пропорциональная зависимость между напряжением Uд и углом поворота вала редуктора. Поэтому изменение расхода воды пропорционально величине отклонения температуры воды от заданного значения. При непрерывном изменении температуры поливной воды процесс регулирования идет непрерывно. Если температура установится, то при правильно подобранных параметрах регулятора процесс регулирования через некоторое время закончится, и вся система придет в новое установившиеся состояние. В результате рассмотрения устройства и работы системы можно сделать следующие выводы: В системе реализован принцип управления по отклонению (ошибке). Система является стабилизирующей. 3 Составление структурной схемы САР температуры поливной воды в теплице Структурной схемой называется наглядное графическое изображение математической модели (математического описания) системы. На структурной схеме каждое звено изображается прямоугольником, внутри которого записывается математическое описание звена. Связи между звеньями структурной схемы изображаются линиями со стрелками, соответствующие направлению прохождения сигналов. Над линиями ставятся обозначения сигналов. Составим структурную схему САР температуры поливной воды в теплице. 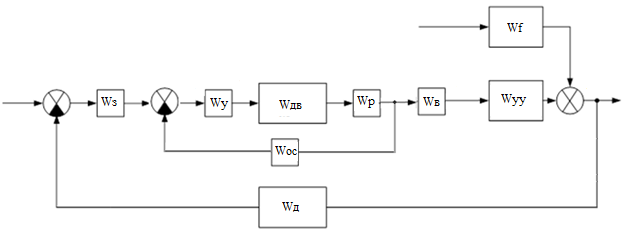 Рис.3. Структурная схема САР температуры поливной воды в теплице из передаточных функций 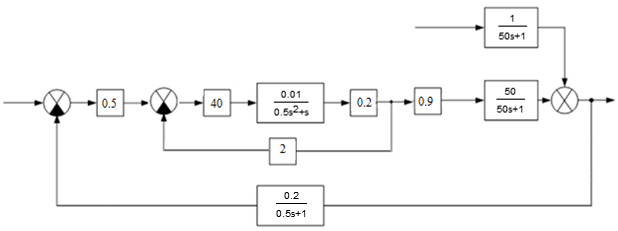 Рис.4 Структурная схема САР температуры поливной воды в теплице в численном виде Передаточные функции всех элементов системы: 1.Уравнение скоростного водонагревателя, как объекта управления: 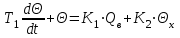 где Θ – температура поливной воды, оС; Q в – расход воды проходящей через, водонагреватель, м3/ч; Θх – температура холодной воды, оС; Изображение Лапласа этого уравнения: 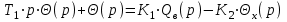 Передаточная функция по управляющему воздействию: 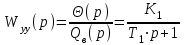 ,Передаточная функция по возмущающему воздействию: 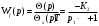 ,Аналогичным образом получим передаточные функции остальных элементов системы: 2. Датчик (термометр сопротивления c измерительным блоком): 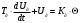 , где Θ – измеряемая температура, оС; Uд– напряжение на выходе измерительного блока, Ом; 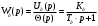 , 3. Задатчик: 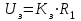 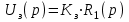 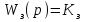 4. Дифференциальный усилитель: 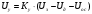 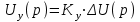 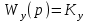 ,6. Двигатель: 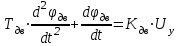 ,  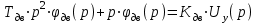,  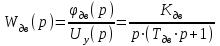,7. Редуктор: 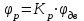 ,  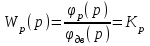, 8. Устройство обратной связи: 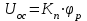 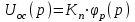 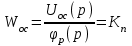 8. Регулирующий орган (вентиль для жидкости): 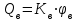 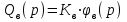 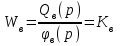 где φв - угол поворота заслонки вентиля, рад Qв – расход горячей воды проходящей через водонагреватель. 4 Построение математической модели системы На основе полученных передаточных функций звеньев составим математическую модель в Simulink. 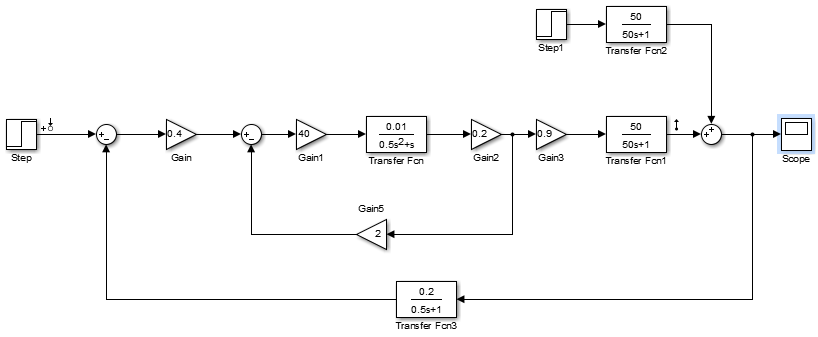 Рис.5 Математическая модель САР температуры поливной воды в теплице 5 Анализ характеристик математической модели системы Устойчивость - это свойство системы возвращаться в исходный или близкий к нему установившийся режим после снятия воздействия, вызвавшего выход из установившегося режима. Устойчивость является очень важной характеристикой качества систем и устройств, применяемых в самых различных областях техники. Условия устойчивости формулируются в виде различных критериев устойчивости, каждый из которых применяют в зависимости от того, какими исходными характеристиками и данными располагают. 5.1 Выходная (временная) характеристика Выходная, или временная характеристика f(t) представляет собой график изменения во времени выходной величины звена. На графике выходной (временной) характеристики показываются такие параметры, как пиковое значение (peak amplitude), время нарастания (rise time) и переходного процесса (setting time) и установившееся состояние (final value). Установившееся значение – это значение сигнала, после завершения переходного процесса. Пиковое значение – это максимальное значение сигнала. Время нарастания – это время, необходимое для достижения 95% конечного значения. Время переходного процесса – это время, спустя которое, сигнал не отклоняется более чем на 5% от установившегося значения. 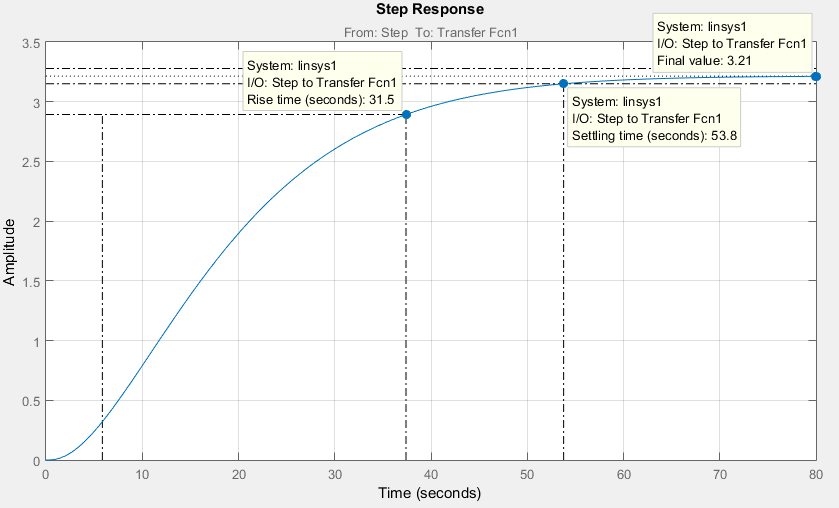 Рисунок 6 – Выходная (временная) характеристика По графику можно определить следующие параметры системы: Peak amplitude (пиковое значение) = 3.21; Rise time (время нарастания) = 31.5 с; Setting time (время переходного процесса) = 53.8 c; Final value (установившееся значение) = 3.21; 5.2 ЛАЧХ и ЛФЧХ ЛАЧХ и ЛФЧХ (диаграмме Боде) — это представление частотного отклика линейной стационарной системы в логарифмическом масштабе. В графике ЛАЧХ представлена зависимость амплитуды (A, дБ) от частоты (f, Гц), а в ЛФЧХ – зависимость фазы выходного сигнала (𝜑, градусы) от частоты (f, Гц). Чтобы определить запас устойчивости по фазе, необходимо опустить перпендикуляр из точки пересечения ЛАЧХ с нулем на ЛФЧХ. На сколько фаза в данной точке отстает от значения -180˚, таков и будет запас устойчивости данной системы по фазе. Чтобы определить запас устойчивости по амплитуде, необходимо опустить перпендикуляр из точки ЛФЧХ с фазой -180˚ на ЛАЧХ. На сколько отличается значение амплитуды в данной точке от значения в точке пересечения графика с нулем, таков запас устойчивости данной системы по амплитуде. 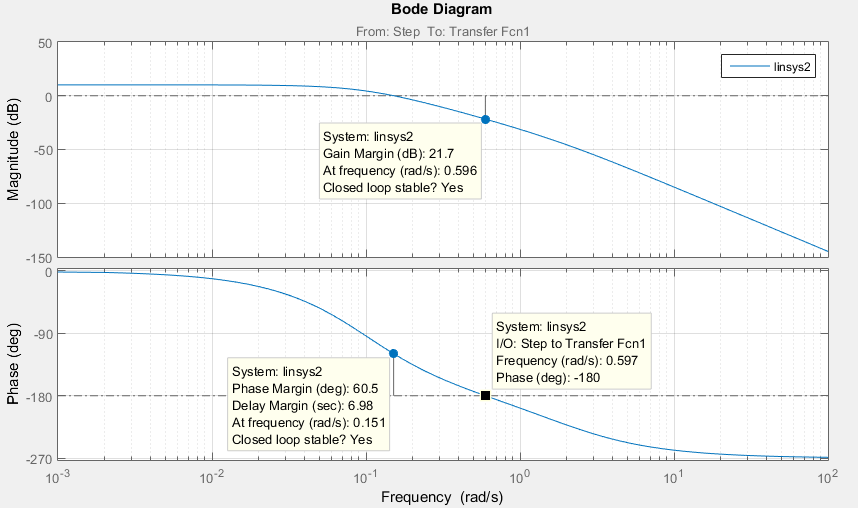 Рисунок 7 – ЛАЧХ и ЛФЧХ Анализируя ЛАЧХ и ЛФЧХ определим запас устойчивости по фазе (Phase Margin) 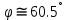 , а также запас устойчивости по амплитуде (Gain Margin) 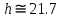 . Также, из графика видно, что частота среза (at frequency) равна 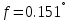 из этого можно сделать вывод о там, что при частотах выше частоты среза амплитуда выходного сигнала системы начинает затухать.5.3 Годограф Найквиста Годограф Найквиста (АФЧХ) — это удобное представление частотного отклика линейной стационарной динамической системы в виде графика в комплексных координатах. На таком графике частота выступает в качестве параметра кривой, фаза и амплитуда системы на заданной частоте представляется углом и длиной радиус-вектора каждой точки характеристики. Годограф Найквиста объединяет на одной плоскости ЛАЧХ и ЛФЧХ. Замкнутая система будет устойчива в том случае, если устойчива разомкнутая система и ее амплитудно-фазовая характеристика не охватывает точку с координатами (-1, j0), называемую критической. Запас устойчивости по Критерию Найквиста: здесь критической является точка (-1; j0), следовательно, вокруг этой точки строится запретная зона, радиус которой будет представлять коэффициент запаса устойчивости. Запасы устойчивости характеризуют удаление годографа АФХ от точки с координатами (-1,j,0). Запас устойчивости по фазе измеряется по дуге окружности единичного радиуса с центром в начале координат между точкой (-1,j,0). И ближайшей к ней точкой годографа АФХ. Частота пересечения годографа АФХ и единичной окружности называется частотой среза. Запас по фазе обеспечивает сохранение устойчивости, при возрастании запаздывания в системе. Запас устойчивости по амплитуде изменяется по действительной полуоси между точкой (-1,j,0) и точкой пересечения с годографом АФХ. Запас по амплитуде обеспечивает сохранение устойчивости при возрастании коэффициента усиления системы. 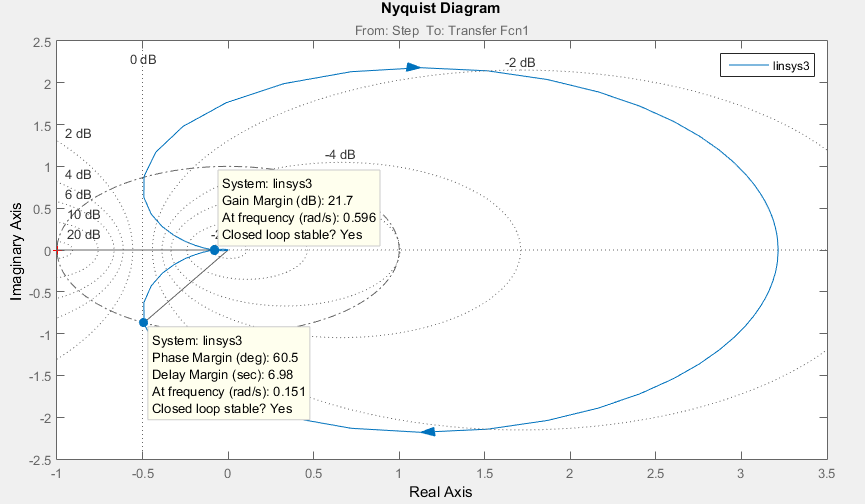 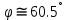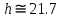Рисунок 8 – Годограф Найквиста При анализе графика видно, что запас устойчивости по фазе (Phase Margin) равен , запас устойчивости по амплитуде (Gain Margin) , что было определено ранее другими способами. На диаграмме отчетливо видно, что годограф не охватывает критическую точку (-1; j0), следовательно, можно сделать вывод – система устойчива.С помощью Matlab определили запас устойчивости по фазе и амплитуде, откуда видно, что они совпадают со значениями на графиках ЛАЧХ, ЛФЧХ, годографа Найквиста. 5.4 Нули и полюса Передаточные функции содержат особые точки на комплексной плоскости – нули и полюса. Полюса – это те значения S, при которых передаточная функция превращается в бесконечность. Для определения полюсов необходимо собственный оператор (знаменатель передаточной функции) приравнять к нулю и произвести решение алгебраического уравнения относительно S. Нули – это те значения S, при которых передаточная функция равна нулю. Для нахождения нулей числитель передаточной функции приравнивается к нулю, и полученное алгебраическое уравнение решается относительно S. Для того, чтобы САР была устойчивой, необходимо и достаточно, чтобы все полюсы передаточной функции замкнутой системы находились в левой полуплоскости комплексного переменного. Наличие хотя бы одного полюса в правой полуплоскости – система неустойчива. Если хотя бы один полюс находится на мнимой оси, то система находится на границе устойчивости. Граница устойчивости обозначается штриховкой в сторону области устойчивости. 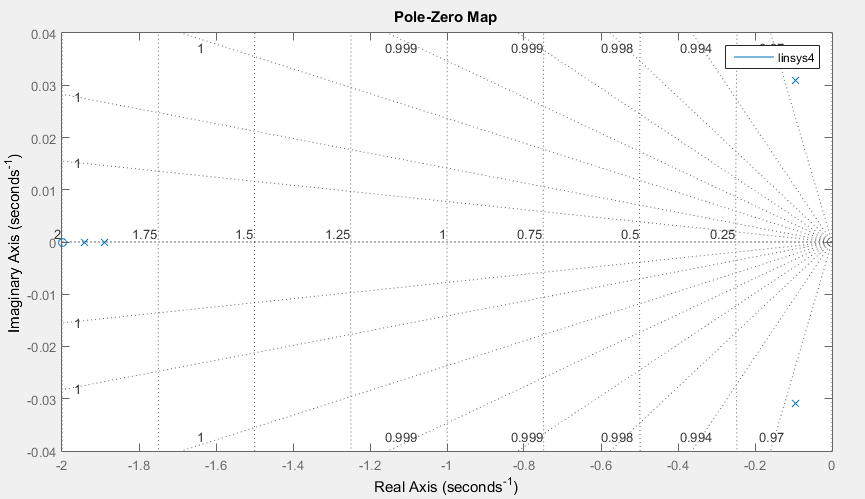 Рисунок 9 – Нули и полюса передаточной функции системы Из этого графика можно сделать вывод о том, что система устойчива, так как полюсы функции лежат в левой полуплоскости. Заключение В результате выполнения курсовой работы была исследована система автоматического регулирования температуры поливной воды в телице. Были составлены структурная схема и математическая модель САР в пакете Simulink. Также были получены передаточные функции для каждого элемента системы. Был проведен анализ устойчивости системы в среде Matlab с использованием выходной характеристика системы, ЛАЧХ, ЛФЧХ, годографа Найквиста, графика нулей и полюсов. По полученным графикам был сделан вывод о том, что система является устойчивой, а также определены запасы устойчивости системы по амплитуде – 21,7 Дб, и по фазе – 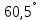 |