итоговое мат. итоговое. Область определения функции Точек разрыва нет
 Скачать 103.36 Kb. Скачать 103.36 Kb.
|
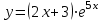 . .Область определения функции: 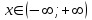 . . Точек разрыва нет. Так как 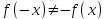 и и 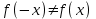 , то функция является ни четной и нечетной, график данной функции имеет общий характер. , то функция является ни четной и нечетной, график данной функции имеет общий характер.Функция непериодическая. Найдем точки экстремума и интервалы монотонности Для этого найдем первую производную от заданной функции и приравняем ее к нулю. 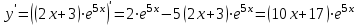 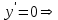 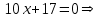 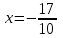 . .Снесем данные в таблицу:
При 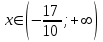 - возрастает. При - возрастает. При 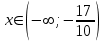 - убывает. - убывает. 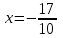 - точка минимума. - точка минимума.Найдем точки перегиба и интервалы выпуклости и вогнутости. Для этого найдем вторую производную от заданной функции и приравняем ее к нулю 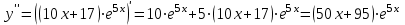 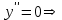 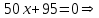 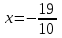 . . Снесем данные в таблицу:
При 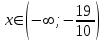 график функции выпуклый, при график функции выпуклый, при 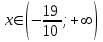 - график функции вогнутый. - график функции вогнутый.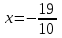 - точка перегиба. - точка перегиба.Найдем наклонные асимптоты Исследуем при 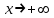 . .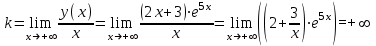 При 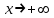 горизонтальных и наклонных асимптот нет. горизонтальных и наклонных асимптот нет.Исследуем при 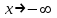 . .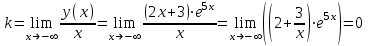 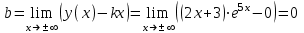 Следовательно, при 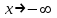 , , 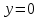 - горизонтальная асимптота, наклонных асимптот нет. - горизонтальная асимптота, наклонных асимптот нет.Найдем точки пересечения с координатными осями: 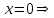 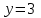 . .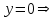 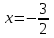 . .График 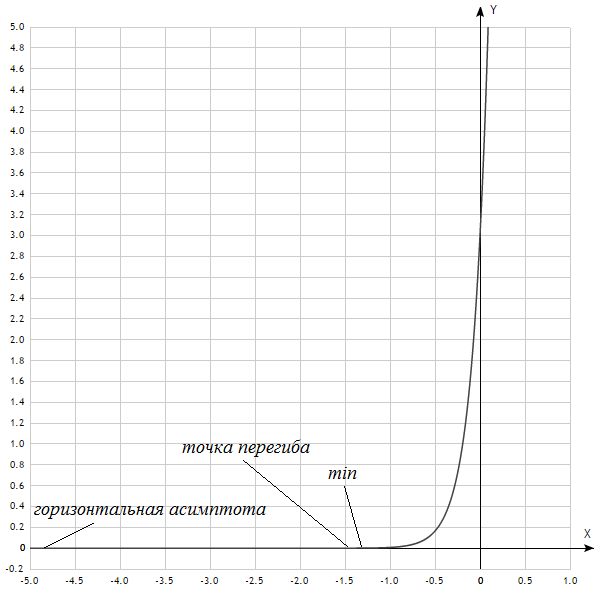 Используя свойства определенного интеграла, искомая площадь будет равна: 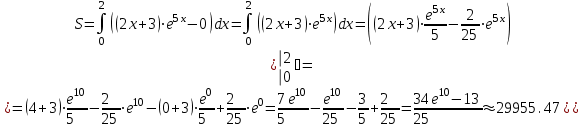 (условных квадратных единиц). (условных квадратных единиц).Полученные результаты в таблице:
|

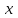
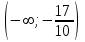
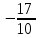
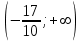
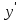
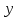
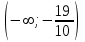
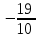
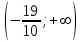
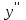
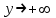
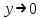
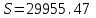 условных квадратных единиц.
условных квадратных единиц.