Мори лабораторная. Мори лаба 2, МРЭТн 21-2. Обработка результатов измерений методом наименьших квадратов

• Название: Обработка результатов измерений методом наименьших квадратов
• Анкор: Мори лабораторная
• Дата: 03.03.2022
• Размер: 0.68 Mb.
• Имя файла: Мори лаба 2, МРЭТн 21-2.docx
• Тип: Лабораторная работа; #381765

Некоммерческое Акционерное Общество

«АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ» им. Г.Даукеева

Кафедра Телекоммуникационных сетей и систем

Лабораторная работа №2

на тему: «Обработка результатов измерений методом наименьших квадратов»

Дисциплина: Математическая обработка результатов измерений в телекоммуникационных системах

Специальность: 5В071900 – Радиотехника, электроника и телекоммуникации

Выполнил:

Группа: МРЭТн 21-2

Вариант: 2

Приняла: к.ф-м.н доцент Хизирова М.А.

___________________ «_____»__________2021 г.

Алматы 2021

Лабораторная работа №2. Обработка результатов измерений методом наименьших квадратов.

Исходные данные:

Таблица 1 – Данные для 1 задания

Xi	1	2	3	4	5	6
Yi	5,2	6,3	7,1	8,5	9,2	10,0

Таблица 2 – Данные для 2 задания

Xi	-3	-1	0	1	3
Yi	-4	-0,8	1,6	2,3	1,5

Проектное задание

1. Найти линейную аппроксимацию данных по методу наименьших квадратов.

2. Приблизить данную функцию многочленом 2-ой степени.
Выполнение задания:

Рассмотрим теперь возможности пакета MatLab для реализации метода наименьших квадратов.

Коэффициенты аппроксимирующего полинома



Сумм=((y-f(x))^2

степени N, наилучшим образом приближающего таблицу функций Y(X) в смысле наименьшего квадратичного отклонения в узлах, находятся с помощью функции

P = polyfit (X, Y, N).

Для вычисления значений полинома можно использовать функцию:

Y = polyval (P, X),

где вектор Xпоказывает интервал табличных значений и может даже выходить за его пределы. Тем самым интерполяционный полином будет использован также для экстраполяции данных.

Рассмотрим пример, реализующий данный пример:

X=[0.050.100.170.250.300.36];

Y=[0.05000.10030.17170.25530.30930.3764];

xlabel('X');

ylabel ('Y');

hold onplot(X,Y,'ko')

t=-0.05:0.01:0.45;

c5=polyfit(X,Y,5);

y5 = polyval(c5, t);

plot(t,y5,'k-')

title('Plynomapproximation')

legend('Data','Approx.',0)


Рисунок 1 – Данные функции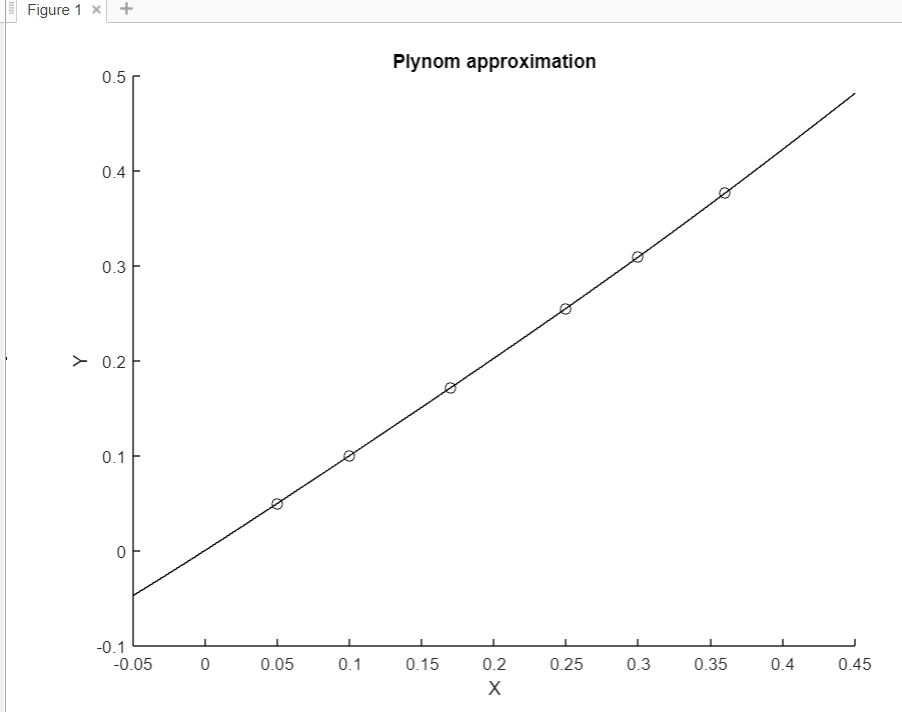



Рисунок 2 – График функции polyfit

Вставив значения Х, У по заданному варианту, получаем следующую функцию:



Рисунок 3 – Данные для функции по заданию №1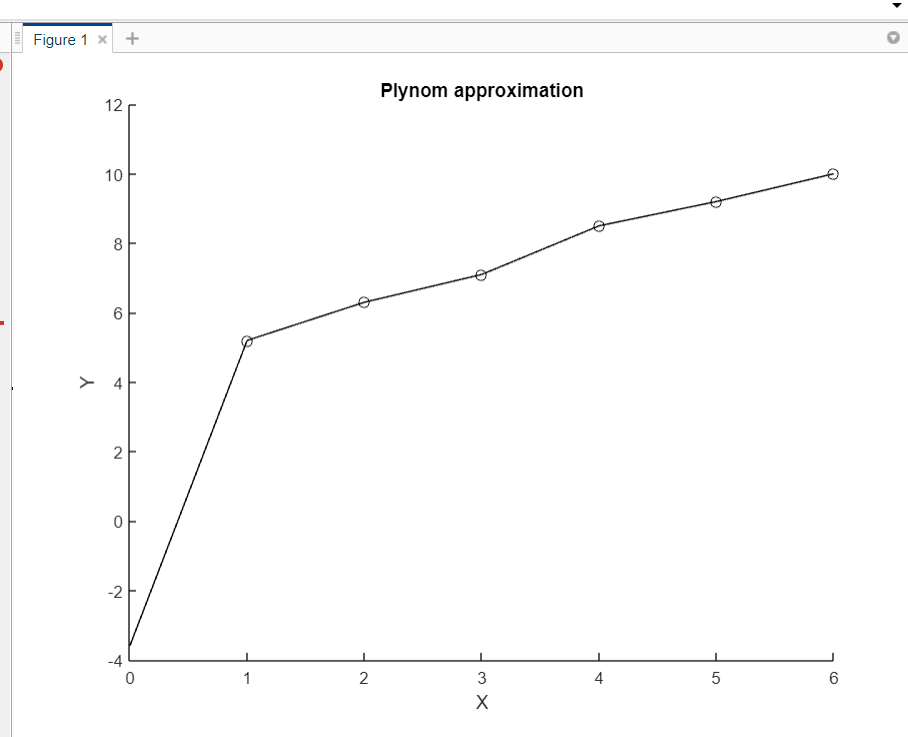



Рисунок 4 – График функции polyfit для №1 задания

В рисунке 2 отражающий результат работ программы, показывает, что в данном примере качество интерполяции, а также экстраполяции в выбранном диапазоне, весьма хорошее.

Однако при других исходных данных качество может оказаться значительно хуже, как показано в рисунке 4. Существенным аспектом при полиномиальной аппроксимации является выбор степени полинома.

Задание №2:

X = [-2, -1, 0, 1, 2];

Y = [0 0 1 0 0];

xlabel ('X');

ylabel ('Y'); hold on

plot (X,Y,'ko')

t = -3:0.1:3;

c2 = polyfit (X,Y,2);

y2 = polyval (c2,t);

plot (t,y2,'k:')

c4 = polyfit (X,Y,4);

y4 = polyval (c4,t);

plot(t,y4,'k-')

legend('Data','poly 2 degree', 'poly 4 degree',0)



Рисунок 5 – Данные для функции по значениям №2 задания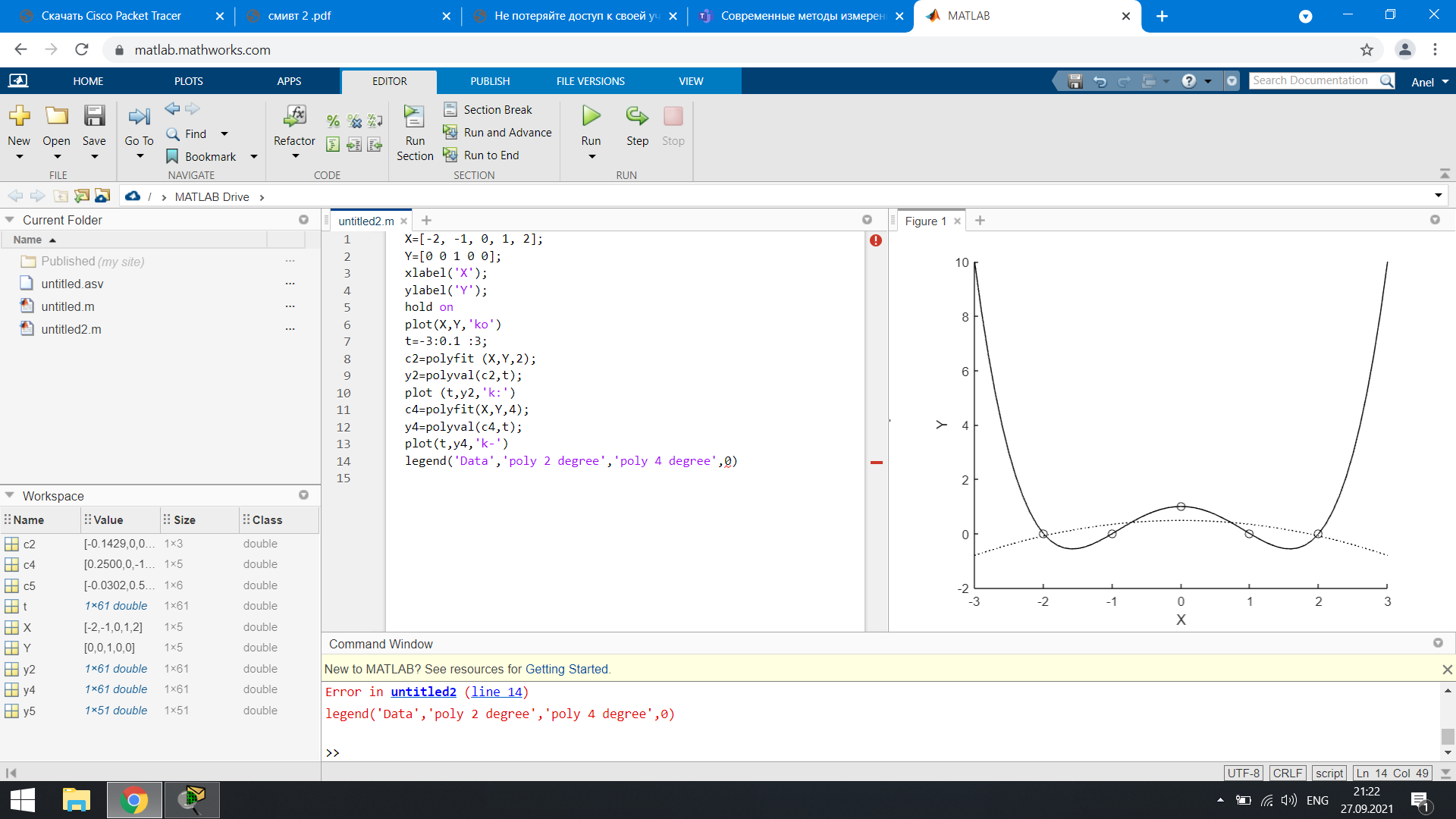



Рисунок 6 – Интерполяция полиномами разной степени
Если интерполяционный полином 4-й степени проходит через табличные узлы аппроксимируемой функции, то полином 2-й степени через эти узлы уже не проходит, но среди всех полиномов 2-й степени он дает наименьше среднеквадратичное отклонение в узлах табличной функции (рисунок 6).

Заключение

Целью данной лабораторной работы было обработка результатов измерений методом наименьших квадратов в программной среде MATLAB.

Метод наименьших квадратов – математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных.

Данная лабораторная работа состоит из 2 заданий. В задании №1 было необходимо найти линейную аппроксимацию данных по методом наименьших квадратов используя функцию polуfit. Данная функция вычисляет коэффициенты полинома р(х) степени n. Это называется аппроксимированным коэффициентом. При выполнении задания №1 были приведены 2 функции с разными интерполяциями и с экстрополяциями. В первом случае (рисунок 2) имеется график с хорошей интерполяцией и экстрополяцией, а во втором случае качество весьма хуже. Существенным аспектом при полиномиальной аппроксимации является выбор степени полинома.

По 2 заданию был получен результат интерполяции полиномами различной степени выраженности. Интерполяция – это точное нахождение любой величины по известным заданным значениям определенной величины или другими связанными с ней величинами.