Контрольная. ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ МНОГОКРАТНЫХ РАВНОТОЧНЫХ ИЗМЕРЕНИЙ.. Обработка результатов прямых многократных равноточных

• Название: Обработка результатов прямых многократных равноточных
• Анкор: Контрольная
• Дата: 04.10.2022
• Размер: 2.23 Mb.
• Имя файла: ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ МНОГОКРАТНЫХ РАВНОТОЧНЫХ ИЗМЕРЕНИЙ..docx
• Тип: Документы; #712952

ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ МНОГОКРАТНЫХ РАВНОТОЧНЫХ ИЗМЕРЕНИЙ

1.Обработать прямые многократные равноточные измерения (в соответствии с п.3). Исходные данные приведены по вариантам в таблице 1. При этом считать, что в результатах наблюдений исключены все известные систематические погрешности.

Таблица 1 - Исходные данные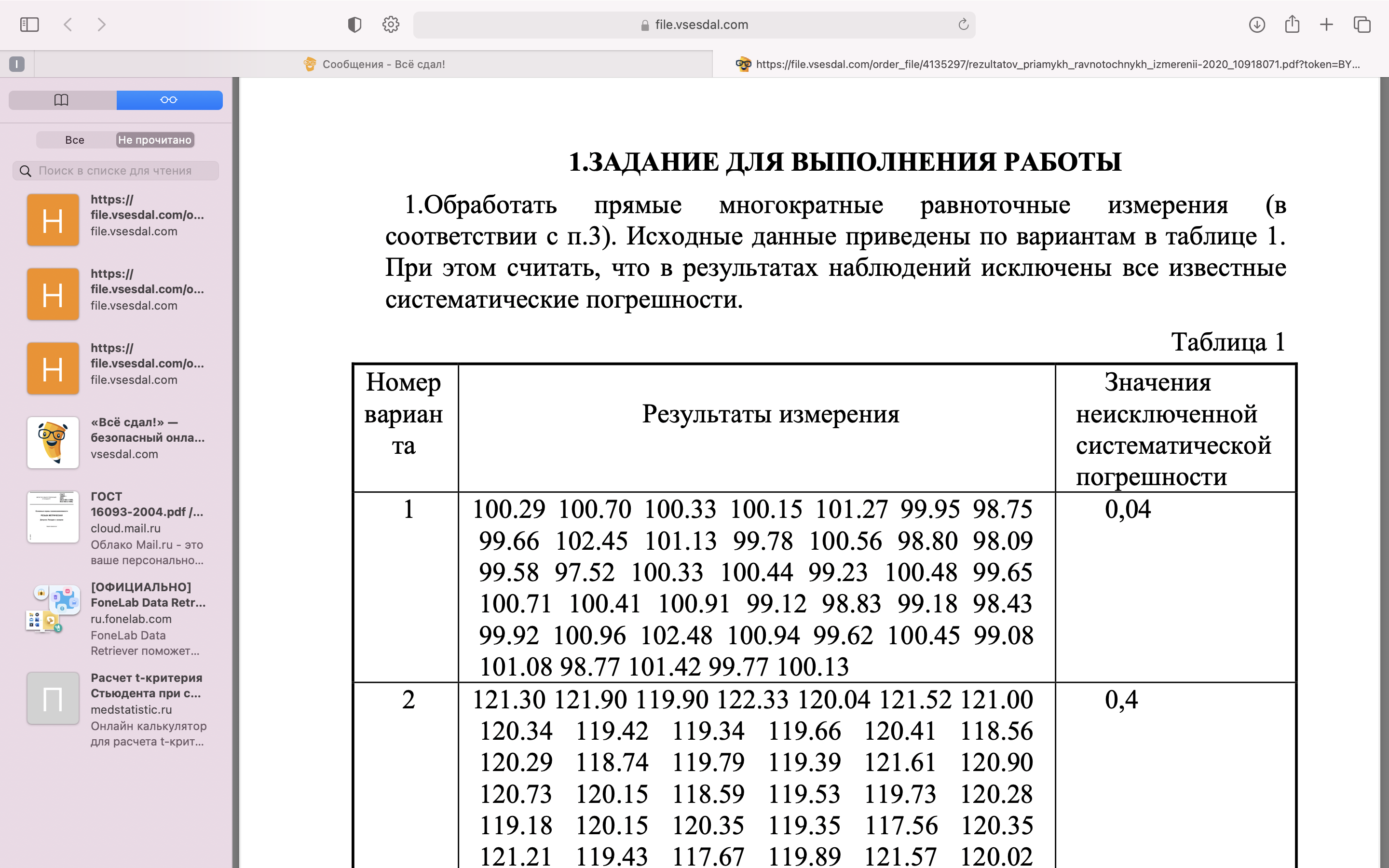



Порядок выполнения работы:

1. 
   Исключение систематических погрешностей
   

Математическое ожидание результатов наблюдения: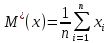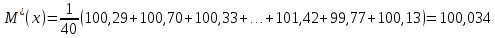





где x_i – результат _i –ого измерения;

n – число результатов наблюдений.

2. 
   Среднее квадратическое отклонение результатов наблюдения: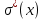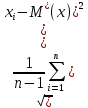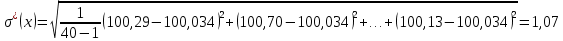
   

=

3. 
   Проверка на наличие грубых погрешностей:
   

Расположим результаты измерения в порядке возрастания:

Таблица 2 – Ранжированный ряд

97,52	100,13
98,09	100,15
98,43	100,29
98,75	100,33
98,77	100,33
98,8	100,41
99,08	100,44
99,12	100,45
99,18	100,48
99,23	100,56
99,58	100,7
99,62	100,71
99,65	100,91
99,66	100,94
99,77	100,96
99,78	101,13
99,92	101,27
99,95	101,42
100,08	102,45

t_гр =3,557, вычисляем x_гр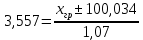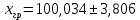



t_гр.н = 96,228 t_гр.в = 103,840

Следовательно, в ряду наблюдений грубых ошибок не обнаружено.

5. Среднеквадратичное отклонение результата измерений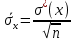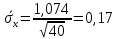





6.Проверка гипотезы о принадлежности результатов наблюдений к нормальному распределению

Так как n=40, то проверка гипотезы производится по составному критерию.

Критерий 1.

Вычисляется отношение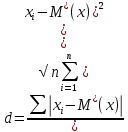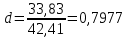





Условие d_1g1/2 d d_g1/2 (0,74550,79770,8559) выполняется, следовательно, гипотеза о нормальном распределении по критерию 1 принимается при уровне значимости g₁=5%.

Критерий 2.

Число степеней свободы r1037, выбранного уровня значимости g₂ =5%, значимости составного критерия g  g₁  g₂ =10%.

Z_/2 r0,9876,86 для Результирующий уровень

Следовательно, принимается гипотеза о нормальности распределения по составному критерию.

7. Границы доверительного интервала случайной погрешности результата измерений

 t_x.

Для вероятности P=0,95 коэффициент t берется равным 2,09, тогда интервал определяется как

 1,970,17 0,335,

Mxx_ист Mx.

99,698  x_ист  100,368

8. Границы неисключенной систематической погрешности m10,04.

9. Границы доверительного интервала суммарной погрешности

Отношение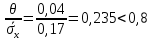

  0,335.

10. Окончательный результат измерения

x 100,033 0,335, после округления x 100,03 0,34 при P=0,95.