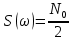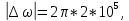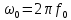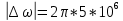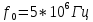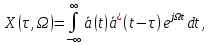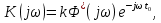Обработка случайных сигналов
 Скачать 374.75 Kb. Скачать 374.75 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра ЭУТ Курсовая РАБОТА по дисциплине «Методы анализа и обработки сигнала» Тема: Обработка случайных сигналов
Санкт-Петербург 2023 ЗАДАНИЕ на курсовую работу
Требуется определить: 1. Максимально допустимое значение параметра 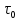 , если ультразвуковой дефектоскоп должен раздельно принимать сигналы от дефектов, отстоящих по глубине на 3 мм по стали. За меру разрешающей способности принимается значение аргумента , если ультразвуковой дефектоскоп должен раздельно принимать сигналы от дефектов, отстоящих по глубине на 3 мм по стали. За меру разрешающей способности принимается значение аргумента 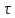 нормированной функции неопределенности при нормированной функции неопределенности при 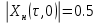 2. Структуру согласованного фильтра и параметры (ширина полосы пропускания и изменение отношения сигнал/помеха на выходе по сравнению со входом) квазиоптимального фильтра, состоящего из 1 колебательного контура. 3. Зависимость 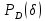 , где , где 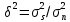 на входе приемного тракта, если обнаружитель выполнен по схеме согласованный фильтр – линейный детектор – пороговое устройство. Результаты сравнить с работой простейшего обнаружителя Неймана -Пирсона. При этом с доверительной вероятностью на входе приемного тракта, если обнаружитель выполнен по схеме согласованный фильтр – линейный детектор – пороговое устройство. Результаты сравнить с работой простейшего обнаружителя Неймана -Пирсона. При этом с доверительной вероятностью 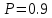 должно быть не более должно быть не более 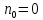 ложного срабатывания регистратора дефектов в ложного срабатывания регистратора дефектов в 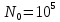 независимых точках контроля. независимых точках контроля.Содержание пояснительной записки: «Содержание», «Введение», «Заключение», «Список использованных источников»)
Аннотация Ультразвуковой дефектоскоп применяется в различных областях, где необходимо обнаруживать дефекты в материалах и конструкциях. Например, он используется в металлургии для контроля качества сварных соединений, в авиации для обнаружения трещин и других дефектов в летательных аппаратах, в медицине для диагностики заболеваний и т.д. В данной курсовой работе было произведено: нахождение параметра, определяющего длительность радиоимпульса с заданной формой огибающей по заданной разрешающей способности, определение параметров квазиоптимального фильтра, максимизирующего отношение сигнал/помеха для заданного сигнала, получена зависимость вероятности правильного обнаружения от отношения сигнал/помеха на выходе по сравнению с входом. SUMMARY Ultrasonic flaw detector is used in various fields where it is necessary to detect defects in materials and structures. For example, it is used in metallurgy to control the quality of welded joints, in aviation to detect cracks and other defects in aircraft, in medicine to diagnose diseases, etc. In this course work, the following was performed: finding a parameter that determines the duration of a radio pulse with a given envelope shape according to a given resolution, determining the parameters of a quasi-optimal filter that maximizes the signal/interference ratio for a given signal, the dependence of the probability of correct detection on the signal/interference ratio at the output compared to the input was obtained. содержание
введение Для выполнения курсовой работы по дисциплине "Методы анализа и обработки сигналов" необходимо применить навыки, полученные при изучении данной дисциплины и предшествующих дисциплин («Основы теории сигналов»). В процессе выполнения курсовой работы и зависимости от полученного задания студенты должны научиться оценивать статистические характеристики случайных процессов по выборочным значениям, приобрести практические навыки расчета характеристик обнаружения сигналов или определения точности измерения параметров, изучить методы построения и расчета параметров оптимальных и квазиоптимальных фильтров, максимизирующих отношение сигнал/помеха, и приобрести навыки определения параметров сигнала на выходе фильтра, освоить способы определения разрешающей способности сигналов и систем, их использующих. 1. ОПРЕДЕЛЕНИЕ ПАРАМЕТРА 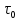 . . Полезный сигнал, поступающий на вход приемного тракта дефектоскопа 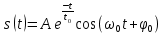 Функция неопределенности задается следующим выражением (1), воспользуемся ей для определения 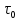 : :
где 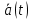 – комплексная огибающая сигнала. – комплексная огибающая сигнала.По условию случайная фаза сигнала равномерно распределена в интервале 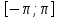 . В связи с этим для вычисления функции неопределенности подставим в формулу выражение для сигнала, в котором за . В связи с этим для вычисления функции неопределенности подставим в формулу выражение для сигнала, в котором за 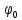 примем среднее значение фазы равное нулю. примем среднее значение фазы равное нулю. 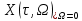 = =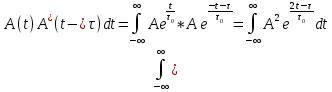 За меру разрешающей способности принимается значение 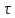 аргумента нормированной функции неопределенности аргумента нормированной функции неопределенности 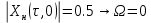 . .Преобразуем подынтегральное выражение 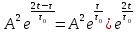 Тогда учитывая, что 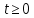 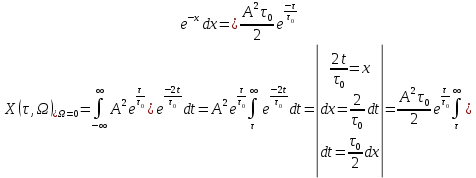 Следовательно, выражение для функции неопределенности примет вид 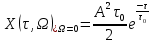 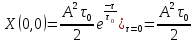 Нормированная функция неопределенности: 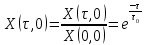 Найдём численное значение параметра 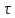 : :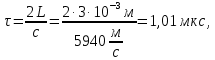 где с – скорость распространения звука в рассматриваемой среде (стали)- 5940м/с, L- расстояния между объектами Подставим это значение в выражение для нормированной функции неопределенности и найдем параметр 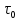 : :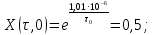 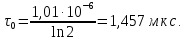 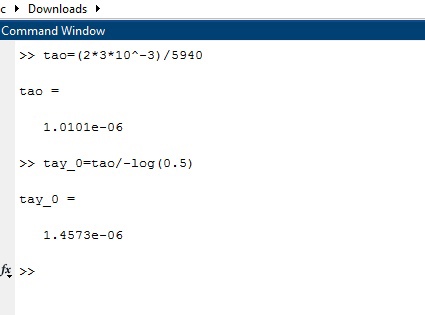 Рисунок 1- Определение длительности сигнала 2. определение структуры согласованного и параметров квазиоптимального фильтра, состоящего из 1 колебательного контура 2.1. Построение согласованного фильтра Комплексная частотная характеристика оптимального фильтра в случае помехи с постоянной спектральной плотностью в диапазоне частот, покрывающем весь спектр сигнала, задается следующей формулой (14):
где 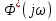 - комплексно-сопряженное значение амплитудного спектра сигнала, k- постоянная. - комплексно-сопряженное значение амплитудного спектра сигнала, k- постоянная.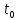 – момент времени, соответствующий окончанию интервала, содержащего основную долю энергии сигнала. – момент времени, соответствующий окончанию интервала, содержащего основную долю энергии сигнала.Проверим второе условие физической реализуемости: 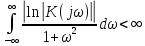 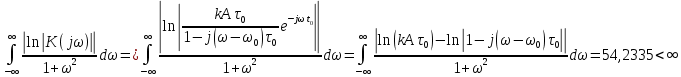 Исходя из того, что интеграл равен числу (Приложение А) первое условие физической реализуемости выполняется. Рассчитаем комплексно-амплитудный спектр сигнала: 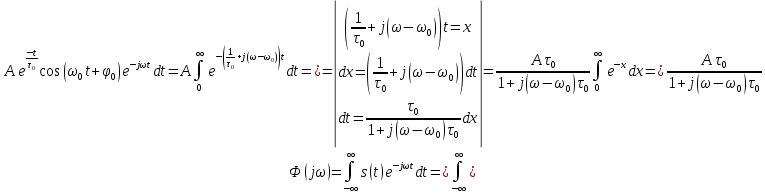 Таким образом, спектр сигнала 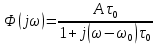 Частотная характеристика согласованного фильтра будет определяться следующим выражением 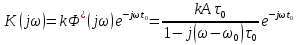 Здесь 𝑡0 выбирается в момент времени, соответствующий окончанию интервала, содержащего основную долю энергии сигнала (0.9𝐸𝑠): 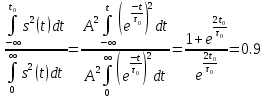 Таким образом, 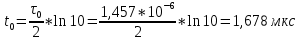 Проверим второе условие реализуемости данного фильтра с помощью импульсной характеристики согласованного фильтра 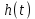 , если фильтр реализуем, то , если фильтр реализуем, то 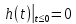 : :ИПФ согласованного фильтра определяется следующим выражением: 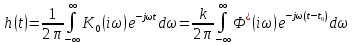 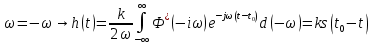 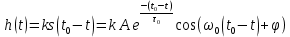 Результат расчета представлен на рисунке 2- условие не соблюдается 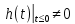 , значит, построение согласованного фильтра невозможно. , значит, построение согласованного фильтра невозможно.  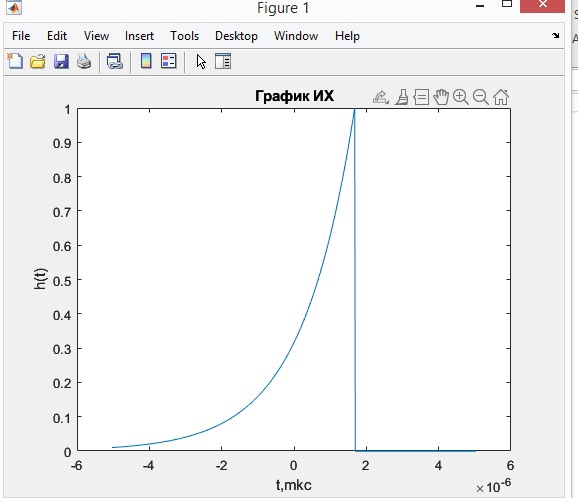 Рисунок 2- Проверка фильтра на физическую реализуемость 2.2 Построение квазиоптимального фильтра Рассчитаем заданный квазиоптимальный фильтр. Его отношение сигнал/помеха на выходе лишь немного меньше значения, рассчитываемого для согласованного фильтра. Тогда ухудшение отношения сигнал/помеха на выходе квазиоптимального фильтра по сравнению с этим отношением на выходе оптимального фильтра равно: 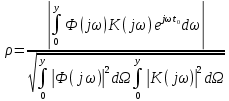 По условию квазиоптимальный фильтр состоит из 1 колебательного контура. Тогда его частотная характеристика равна: 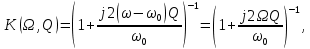 Где 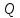 – добротность фильтра, – добротность фильтра, 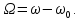 Верхний предел интегрирования 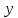 найдем следующим образом (Приложение А). То есть верхний предел интегрирования найдем следующим образом (Приложение А). То есть верхний предел интегрирования 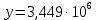 Преобразуем выражение для 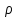 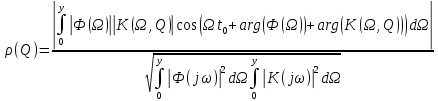 Подставим 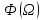 и и 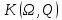 в выражение для в выражение для 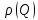 и вычислим и вычислим 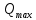 , при котором достигается максимальное отношение сигнал/помеха. На рисунке 2 показана зависимость ухудшения отношения сигнал/помеха на выходе квазиоптимального фильтра от добротности конутра. Вычисления представлены ниже (Приложение А). , при котором достигается максимальное отношение сигнал/помеха. На рисунке 2 показана зависимость ухудшения отношения сигнал/помеха на выходе квазиоптимального фильтра от добротности конутра. Вычисления представлены ниже (Приложение А).Используя вычислительный пакет Matlab получаю максимальное отношение сигнал/помеха 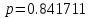 , оптимальная добротность , оптимальная добротность 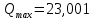 , проигрыш составляет 15,828%. , проигрыш составляет 15,828%.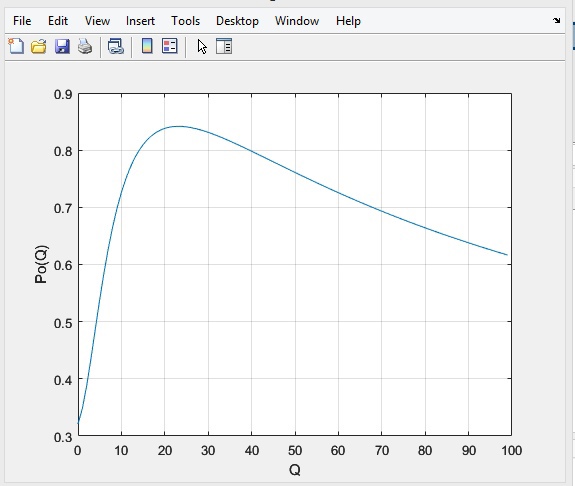 Рисунок 3- Ухудшение отношения сигнал/помеха на выходе Полуширина частотной характеристики одиночного контура: 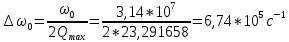 Ширина частотной характеристики одиночного контура: 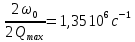 Отношение сигнал/помеха на выходе квазиоптимального фильтра выражается через отношение сигнал/помеха на входе: 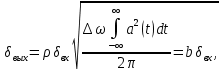 где 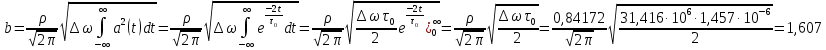 Ниже представлены вычисления (Приложение А). В итоге b=1,607 3. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ОБНАРУЖИТЕЛЯ СИГНАЛА Обнаружитель Неймана-Пирсона соответствует обнаружению очень короткого сигнала. При обнаружении сигналов конечной длительности, если не требуется очень высокое быстродействие, целесообразно строить обнаружитель так, чтобы использовать полную энергию сигнала. Под простейшим обнаружителем Неймана Пирсона принимается схема линейный детектор – пороговое устройство. В нашей работе используется оптимальный обнаружитель, который помимо порогового устройства включает в себя оптимальный фильтр, который ослабляет помехи. Обнаружитель состоит из следующих блоков: согласованный фильтр (1), линейный детектор (2), пороговое устройство (3). 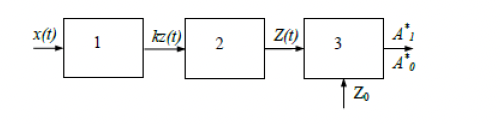 Рисунок 4 – Структура оптимального обнаружителя Формула вероятности правильного обнаружения простейшего обнаружителя Неймана Пирсона: 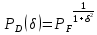 В оптимальном обнаружителе используется фильтр: 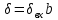 Вероятность правильного обнаружения сигнала оптимального обнаружителя равна: 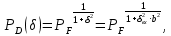 где 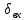 - отношение сигнал/помеха на входе фильтра. - отношение сигнал/помеха на входе фильтра.Вероятность перебраковки 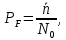 где в числителе стоит среднее количество ложных регистраций определяется из трансцендентного уравнения: 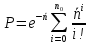 Так как 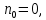 то то 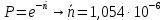 Рассчитаем вероятность ложной тревоги, зная по исходным данным N0 = 106: 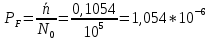 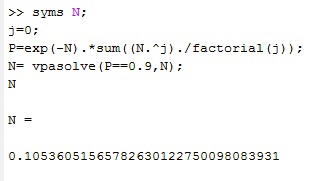 Рисунок 5- Нахождение среднего количества ложных регистраций На рисунке 6 изображены характеристики обнаружения для оптимального обнаружителя и для обнаружителя Неймана-Пирсона. 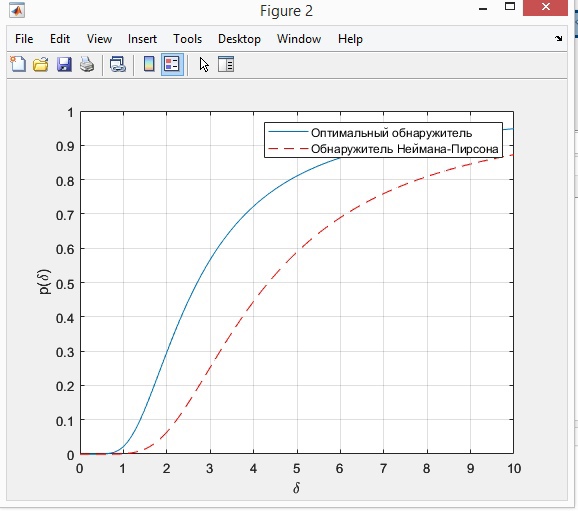 Рисунок 6- Зависимость вероятности правильного обнаружения от отношения сигнал/помеха на входе приемного тракта ЗАКЛЮЧЕНИЕ Максимально допустимое значение параметра 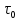 , если ультразвуковой , если ультразвуковойдефектоскоп должен раздельно принимать сигналы от дефектов, отстоящих по глубине на 3 мм по стали, составляет 1,457 мкс. Исходя из того, что 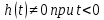 , можно сделать вывод, что построение согласованного фильтра невозможно. Нами был построен квазиоптимальный фильтр, состоящий из 1 колебательного контура, близкий по отношению сигнал/помеха к согласованному. Ширина полосы пропускания фильтра составляет 0,216 МГц. Оптимальное значение добротности составляет 23,001, а значение коэффициента b= 1,607. , можно сделать вывод, что построение согласованного фильтра невозможно. Нами был построен квазиоптимальный фильтр, состоящий из 1 колебательного контура, близкий по отношению сигнал/помеха к согласованному. Ширина полосы пропускания фильтра составляет 0,216 МГц. Оптимальное значение добротности составляет 23,001, а значение коэффициента b= 1,607.Определили зависимость 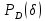 на выходе приёмного тракта, при этом на выходе приёмного тракта, при этомсреднее количество ложных регистраций 0,1054, вероятность перебраковки 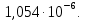 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ А. Б. Сергиенко. Цифровая обработка сигналов: Учеб. Пособие/ЛЭТИ., 2011 – М.: Высшая Школа, 1979/1991. Н. А. Быстрова, Д. Д. Добротин, Е. Л. Шейнман, Анализ и обработка сигналов: Учеб. Пособие/ЛЭТИ.Л., 2018. Д. Д. Добротин, Н.А. Зайцева, С. И. Коновалов. Обработка случайных сигналов:Учеб. пособие/ЛЭТИ. Л., 2016 Добротин Д. Д., Пигулевский Е. Д. Случайные сигналы и помехи в системах интроскопии: Учеб.пособие / ЛЭТИ. Л., 1990. Приложение А l = 3*10^-3; c = 5940; tao = (2.*l)/c; % Определение длительности сигнала tao_0 = tao/-log(0.5); 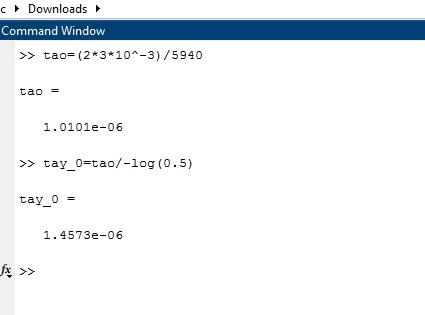 % Построение графика импульсной характеристики Sp = @(t) (exp(-t./tao_0) .* heaviside(t)) » t_0=1.678e-06; » tao_0=1.4573e-06; » t = -3 * t_0 : t_0 / 100 : 3 * t_0; » plot(t, Sp(t_0-t)) » title('График ИХ') » xlabel('t,mkc') » ylabel('h(t)') f0 = 5e6; w0 = 2*pi*f0; deltaw = 2*pi*5e6; n = 1; %число несвязанных колебательных контуров P = 0.9; %Доверительная вероятность n0 = 0; %Число ложных срабатываний N0 = 1e5;%число импульсов l = 3e-3;%разрешающая способность tau0 =1.4573e-06; t0 = (tau0/2)*log(10); syms w J = tau0/(1-1i*(w-w0)*tau0)*exp(-1i*w*t0); Phr = double(vpaintegral(abs(log(abs(J)))/(1+w^2),w,[-inf inf])) %Проверка условия физической реализуемости фильтра tau0 =1.4573e-06; t0 = (tau0/2)*log(10); syms y omega F = tau0/(1+1i*omega*tau0); X = int(abs(F)^2,omega,[0 y])/int(abs(F)^2,omega,[0 deltaw/2]); y = solve(X-0.9,y); fprintf('Верхний предел y = %f рад/c\n', y); syms Q Po Fi K = 1/sqrt(1+(2*omega*Q/w0)^2)^n; Fi = -n*atan(2*omega*Q/w0); Po = abs(vpaintegral(abs(F)*K*cos(omega*t0+angle(F)+Fi),omega,[0 y]))/sqrt(vpaintegral(abs(F)^2, omega, [0 y])*vpaintegral(K^2, omega, [0 y])); q = 0.001:1:100; r =(subs(Po, {Q}, {q})); plot(q, r); grid on; xlabel('Q'); ylabel('Po(Q)'); hold off; [m_ro, idx] = max(r); Qmax = q(idx); fprintf('Qmax = %f \nПроигрыш = %f %% \n', Qmax, (1-m_ro)*100); fprintf('p=%f\n', p); b = 1.607; Pf = 0.1054/N0; delta = 0:0.1:10; P = Pf.^(1./(1+b^2*delta.^2)); Ph = Pf.^(1./(1+delta.^2)); figure plot(delta, P); grid on; xlabel('\delta'); ylabel('p(\delta)'); hold on; plot(delta, Ph, 'r--') legend('Оптимальный обнаружитель', 'Обнаружитель Неймана-Пирсона'); 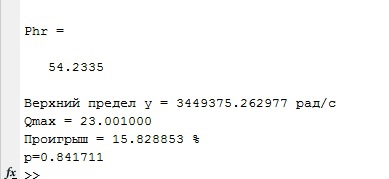 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

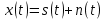
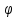 – случайная начальная фаза, распределенная по закону P(
– случайная начальная фаза, распределенная по закону P(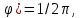
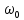 – круговая частота.
– круговая частота.