Разработка веб служб. Разработка Web-служб_230112_ (3). Образования российской федерации
 Скачать 220.69 Kb. Скачать 220.69 Kb.
|
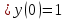 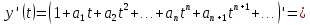 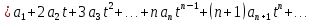 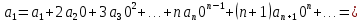 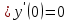 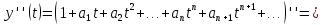 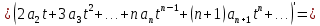 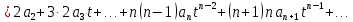 Подставляя в уравнение 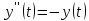 вместо вместо 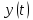 и и 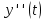 соответствующие степенные ряды, получаем: соответствующие степенные ряды, получаем: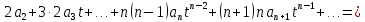 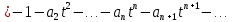 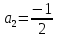 Аналогично вычисляются остальные коэффициенты степенного ряда: 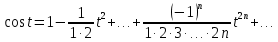 Это равенство означает, что для любого значения аргумента 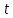 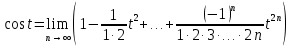 На практике степенной ряд заменяют многочленом: 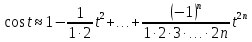 Можно показать, что в этом случае погрешность вычислений не превосходит 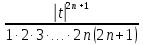 Точно так же разлагается в степенной ряд синус: 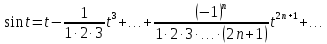 Разложение функции в степенной ряд позволяет вычислять её значения с любой заданной точностью. Гармонические колебания Гармоническим колебанием называется изменение значений физической величины 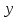 с течением времени с течением времени 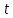 , которое описывается функциональной зависимостью , которое описывается функциональной зависимостью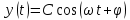 Период косинуса равен 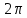 , следовательно, период гармонического колебания равен , следовательно, период гармонического колебания равен 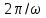 . Действительно, если . Действительно, если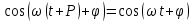 то 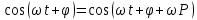 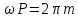 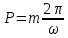 Параметр 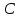 называется амплитудой гармонического колебания (следует отличать амплитуду гармонического колебания называется амплитудой гармонического колебания (следует отличать амплитуду гармонического колебания 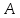 от значения его амплитуды в момент времени от значения его амплитуды в момент времени 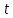 , которое равно , которое равно 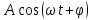 ), параметр ), параметр 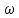 называется круговой, угловой или циклической частотой, в системе СИ единицей измерения круговой частоты служит радиан в секунду (рад/с) или секунда в минус первой степени (с-1), размерность угловой частоты – T-1. Параметр называется круговой, угловой или циклической частотой, в системе СИ единицей измерения круговой частоты служит радиан в секунду (рад/с) или секунда в минус первой степени (с-1), размерность угловой частоты – T-1. Параметр 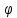 называется начальной фазой гармонического колебания. называется начальной фазой гармонического колебания.Функциональная зависимость 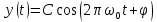 описывает периодическое колебание с частотой 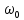 . .Применяя формулу косинуса суммы, получим: 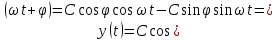 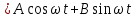 где 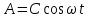 и и 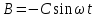 . .Обратно, пусть 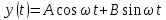 Положим 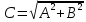 тогда 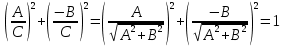 следовательно, существует такое вещественное число 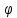 , что, , что, 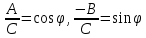 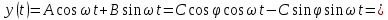 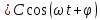 Следовательно, функция 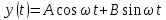 описывает гармоническое колебание, амплитуда которого равна 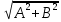 , круговая частота равна , круговая частота равна 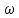 , а начальная фаза , а начальная фаза 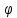 удовлетворяет условиям удовлетворяет условиям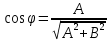 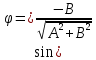 Примечание. Параметр – физическая величина, которая не изменяется в течение некоторого времени. Тригонометрические многочлены Сумма 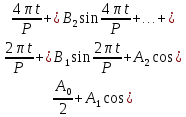 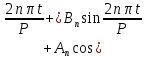 где 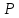 – произвольное положительное число, называется тригонометрическим многочленом. Тригонометрический многочлен является периодической функцией: если прибавить к значению аргумента – произвольное положительное число, называется тригонометрическим многочленом. Тригонометрический многочлен является периодической функцией: если прибавить к значению аргумента 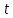 число число 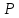 , значение тригонометрического многочлена не изменится. Обычно тригонометрический многочлен пишут со знаком сигма, который заменяет суммирование: , значение тригонометрического многочлена не изменится. Обычно тригонометрический многочлен пишут со знаком сигма, который заменяет суммирование: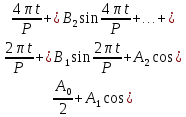 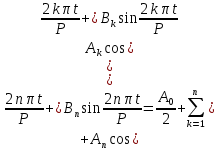 Справедливо следующее утверждение: если функция 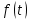 определенна на всей числовой прямой и для любого значения аргумента определенна на всей числовой прямой и для любого значения аргумента 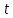 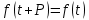 то значение интеграла квадрата разности 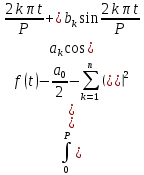 будет минимальным тогда и только тогда, когда 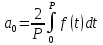 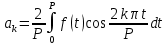 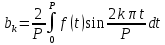 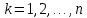 . В этом случае коэффициенты . В этом случае коэффициенты 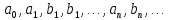 называются коэффициентами Фурье функции называются коэффициентами Фурье функции 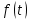 . .В математике квадратный корень из интеграла квадрата разности функций 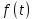 и и 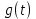 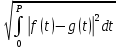 служит оценкой «расстояния» между функциями 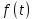 и и 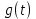 на интервале на интервале 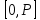 . В этом смысле тригонометрический многочлен является наилучшим приближением функции . В этом смысле тригонометрический многочлен является наилучшим приближением функции 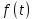 в том и только в том случае, когда его коэффициенты равны соответствующим коэффициентам Фурье этой функции. в том и только в том случае, когда его коэффициенты равны соответствующим коэффициентам Фурье этой функции.Если в точке 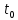 периодическая функция периодическая функция 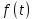 непрерывна, то её ряд Фурье сходится в этой точке к значению функции: непрерывна, то её ряд Фурье сходится в этой точке к значению функции: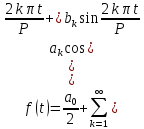 или 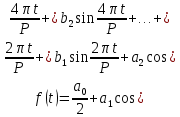 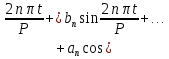 Это означает, что 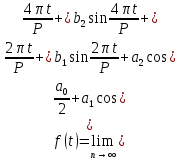 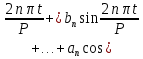 Пример 1. Комнатная электрическая розетка является электромеханическим устройством для электрического соединения и разъединения электрических цепей. В ней два контактных гнезда. Одно из них соединяется с заземлением, его электрический потенциал равен нулю. Другое контактное гнездо обычно называется фазой. Его электрический потенциал изменяется с течением времени. Функциональная зависимость электрического потенциала этого контактного гнезда от времени 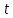 описывается формулой описывается формулой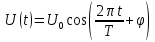 величина 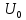 называется амплитудой колебаний электрического потенциала, называется амплитудой колебаний электрического потенциала, 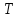 – их периодом. – их периодом. 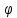 – фазой колебаний. Величина, обратная периоду колебаний называется их частотой: – фазой колебаний. Величина, обратная периоду колебаний называется их частотой: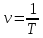 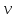 – греческая буква ню. В России используется переменный электрический ток стандартной частоты 50 Гц, в США стандартная частота переменного электрического тока составляет 60 Гц. – греческая буква ню. В России используется переменный электрический ток стандартной частоты 50 Гц, в США стандартная частота переменного электрического тока составляет 60 Гц.Бегущая волна Рассмотрим принципиальную возможность передачи сигнала без искажений. Для простоты предположим, что средой передачи сигнала служит ось 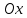 , причём передатчик находится в точке с координатой 0. Обозначим буквой , причём передатчик находится в точке с координатой 0. Обозначим буквой 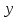 физическую величину, значения которой характеризуют состояние среды. Значения величины физическую величину, значения которой характеризуют состояние среды. Значения величины 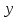 в данной точке являются функциями координаты точки в данной точке являются функциями координаты точки 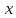 и момента времени и момента времени 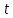 : :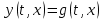 В момент времени 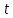 передатчик переводит значение величины передатчик переводит значение величины 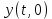 в состояние в состояние 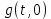 . Сигнал распространяется вдоль оси . Сигнал распространяется вдоль оси 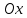 с некоторой скоростью с некоторой скоростью 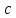 , следовательно, в момент времени , следовательно, в момент времени 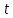 в точке в точке 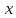 значение величины значение величины 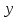 будет таким же, каким оно было в точке 0 в момент времени будет таким же, каким оно было в точке 0 в момент времени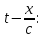 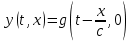 Обычно функцию, стоящую в правой части равенства преобразуют так, чтобы её аргумент стал безразмерным: 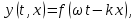 размерность коэффициента 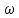 совпадает с размерностью частоты T-1, коэффициент совпадает с размерностью частоты T-1, коэффициент 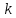 называется волновым числом, его размерность обратна размерности длины L-1. называется волновым числом, его размерность обратна размерности длины L-1.Если значения величины 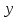 удовлетворяют уравнению, которое мы получили, то говорят, что вдоль оси удовлетворяют уравнению, которое мы получили, то говорят, что вдоль оси 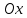 распространяется бегущая волна. Приведённые выше выкладки доказывают, что бегущая волна передаётся без искажений. Действительно, в этом случае приёмник, который находится в точке распространяется бегущая волна. Приведённые выше выкладки доказывают, что бегущая волна передаётся без искажений. Действительно, в этом случае приёмник, который находится в точке 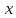 , в момент времени , в момент времени 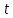 фиксирует то самое значение, которое было в точке 0, где установлен передатчик, в момент времени фиксирует то самое значение, которое было в точке 0, где установлен передатчик, в момент времени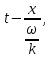 отношение 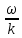 равно скорости распространения сигнала: для любой точки с координатой равно скорости распространения сигнала: для любой точки с координатой 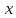 , любого момента времени , любого момента времени 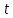 и любого числа и любого числа 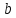 , удовлетворяющих условию , удовлетворяющих условию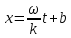 значение 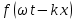 будет одним и тем же – равным будет одним и тем же – равным 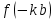 . .Передача электрического сигнала Электрическим сигналом служит сила тока (токовый сигнал) или электрический потенциал (потенциальный сигнал). Для определённости мы будем говорить о потенциальном сигнале, который передаётся по двухпроводной линии, параллельной оси 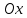 . Линия связи характеризуется погонными (приходящимися на единицу длины) значениями следующих физических величин: индуктивности . Линия связи характеризуется погонными (приходящимися на единицу длины) значениями следующих физических величин: индуктивности 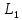 , сопротивления , сопротивления 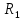 , ёмкости , ёмкости 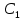 и проводимости изоляции проводов и проводимости изоляции проводов 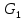 . Индуктивность провода характеризует связь между изменениями магнитного поля электрического тока, текущего по проводу, и силы этого тока, ёмкость характеризует способность провода накапливать электрический заряд. Сила тока . Индуктивность провода характеризует связь между изменениями магнитного поля электрического тока, текущего по проводу, и силы этого тока, ёмкость характеризует способность провода накапливать электрический заряд. Сила тока 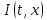 , протекающего через поперечное сечение провода, в точке x в момент времени , протекающего через поперечное сечение провода, в точке x в момент времени 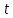 и потенциал и потенциал 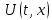 в точке x в момент времени в точке x в момент времени 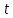 удовлетворяют следующей системе дифференциальных уравнений: удовлетворяют следующей системе дифференциальных уравнений: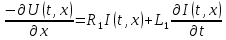 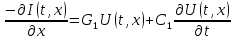 Исследование этих уравнений показывает, что электрический сигнал не может распространяться по проводам в виде бегущей волны, но в том случае, когда значения погонных значений индуктивности, сопротивления, ёмкости и проводимости изоляции пропорциональны: 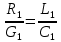 система допускает решение вида 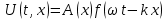 . Так как множитель . Так как множитель 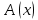 не зависит от времени, приёмник может однозначно восстановить потенциальный сигнал, отправленный передатчиком. Линия передачи электрического сигнала, для которой справедливо условие пропорциональности значений индуктивности, сопротивления, ёмкости и проводимости изоляции, называется линией без искажений. не зависит от времени, приёмник может однозначно восстановить потенциальный сигнал, отправленный передатчиком. Линия передачи электрического сигнала, для которой справедливо условие пропорциональности значений индуктивности, сопротивления, ёмкости и проводимости изоляции, называется линией без искажений.Волновое сопротивление Рассмотрим однопроводную линию связи без искажений: контакты передатчика подключены к узлам 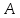 и и 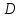 , контакты приёмника подключены к узлам , контакты приёмника подключены к узлам 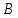 и и 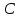 , потенциалы узлов , потенциалы узлов 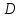 и и 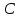 нулевые, узлы нулевые, узлы 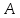 и и  соединены электрическим проводом (рисунок Однопроводную линия связи, файл PP_Разработка Web-служб). На практике нулевой потенциал реализуется с помощью заземления - провода, соединённого с металлической пластиной, закопанной в землю (этот провод называется общим проводом). Будем считать, что при соединены электрическим проводом (рисунок Однопроводную линия связи, файл PP_Разработка Web-служб). На практике нулевой потенциал реализуется с помощью заземления - провода, соединённого с металлической пластиной, закопанной в землю (этот провод называется общим проводом). Будем считать, что при |
