Информационные сети. ИС ЛР№1 Грубляк АДБ-18-07. Образовательная программа 15. 03. 04 Автоматизация технологических процессов и производств Дисциплина Информационные системы
 Скачать 264.84 Kb. Скачать 264.84 Kb.
|
 МИНОБРНАУКИ РОССИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Московский государственный технологический университет «СТАНКИН» (ФГБОУ ВО «МГТУ «СТАНКИН») Институт цифровых интеллектуальных систем Кафедра компьютерных систем управления Образовательная программа 15.03.04 «Автоматизация технологических процессов и производств» Дисциплина «Информационные системы» Лабораторная работа №1 Выполнил: студент гр. АДБ-17-08 __________ Грубляк В.Я. (дата) (подпись) Принял: к.т.н., доцент _____________ Никишечкин А.П. (дата) (подпись) Москва 2021 ОглавлениеЦель работы: 1 Теоретическая часть: 2 Практическая часть. 4 Заключение: 11 Список литературы 12 Цель работы:Проанализировать заданную сеть на безопасность и живость, представить сеть в виде сложной АП-сети, провести анализ на безопасность и живость по старшей компоненте, составить матричное уравнение для проверки достижимости маркировки и составить операторные формулы для заданных позиций. Теоретическая часть:Основные свойства сетей Петри Безопасность Позиция 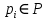 сети Петри C с начальной маркировкой сети Петри C с начальной маркировкой 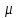 является безопасной, если является безопасной, если 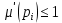 для любой для любой 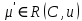 . Иными словами, позиция сети безопасна если число точек в ней никогда не превышает 1. Сеть Петри безопасна если безопасны все позиции сети. . Иными словами, позиция сети безопасна если число точек в ней никогда не превышает 1. Сеть Петри безопасна если безопасны все позиции сети. Ограниченность Расширение свойства безопасности. Позиция является ограниченной если количество точек не превышает определенного значения. k-ограниченность и k-безопасность Позиция 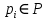 сети Петри C с начальной маркировкой сети Петри C с начальной маркировкой 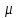 . k-ограничена и k-безопасна, если . k-ограничена и k-безопасна, если 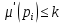 для всех для всех 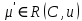 , т.е. позиция сети k-ограничена если количество точек в ней никогда не превышает целое число k. Сеть Петри k-безопасна, если каждая ее позиция k-безопасна, где k-верхняя граница безопасности ее позиций. , т.е. позиция сети k-ограничена если количество точек в ней никогда не превышает целое число k. Сеть Петри k-безопасна, если каждая ее позиция k-безопасна, где k-верхняя граница безопасности ее позиций.Сохранение Точки при срабатывании переходов не исчезают и не создаются, т.е. общее число точек в сети остается постоянным. Сеть Петри C с начальной маркировкой 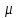 является строго сохраняющей: является строго сохраняющей: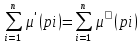 , где n-число позиций в сети , где n-число позиций в сетиИз строгого сохранения следует, что число входов в каждый переход должно быть равно числу выходов 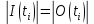 . .Сохранение по отношению к вектору взвешивания Сеть Петри должна сохранять ресурсы, которая она моделирует. Однако строгое соответствие между точками и ресурсами необязательно. В общем случае вводим вес wi композиции pi и вектор взвешивания W= (w1, w2, wn) c целыми компонентами строго большими 0. Сеть Петри с начальной маркировкой 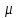 сохраненяющая по отношению к вектору взвешивания, если сумма произведений веса wi и маркировки сохраненяющая по отношению к вектору взвешивания, если сумма произведений веса wi и маркировки 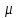 ’ постоянна для всех ’ постоянна для всех 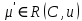 , т.е. , т.е. 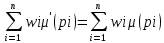 , где n-число позиций в сети. , где n-число позиций в сети.Живучесть Сеть Петри называют живой при заданной начальной маркировке, если а)Для любой пары маркировок ( 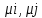 ), принадлежащих множеству ), принадлежащих множеству 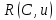 , имеет место , имеет место 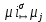 , т.е. существует последовательность , т.е. существует последовательность 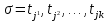 , срабатывание которых переводит сеть из маркировки , срабатывание которых переводит сеть из маркировки 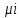 в маркировку в маркировку 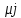 . .б) в множестве 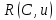 существует пара маркировок ( существует пара маркировок (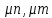 ) имеет место ) имеет место 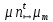 , т.е. срабатывание перехода переводит сеть из маркировки , т.е. срабатывание перехода переводит сеть из маркировки 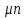 в маркировку в маркировку 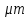 . .Активность Переход активен если он потенциально запустим, в нем нет тупика. Есть маркировка, в которой он сработает. Сеть Петри может быть формально представлена как совокупность множеств: N = (P, T, G, Ω), где P = {p1, p2… pn} – множество всех позиций (n – количество позиций); Т = {t1, t2… tm} – множество переходов (m – количество переходов); G = (Gp-t, Gt-p) – множество дуг сети: Gp-t = (p*t), Gt-p = (t*p) – множества дуг, ведущих соответственно от переходов к позициям и от позиций к переходам (дуг, соединяющих однородные вершины, не существует); Ω = {ω1, ω2… ωk} – множество весов дуг (k – количество дуг). Инструменты анализа сетей Петри Древо достижимости – содержит множество достижимости и представляет собой граф, вершины которого маркировки, а дуги – переходы; при срабатывании переходов данная маркировка изменяется на новую. Матричный метод. Вводятся две матрицы, характеризирующие входные и выходные функции, а также матрицу разности этих функций. Такая матрица не полностью отражает структуру сети Петри и не дает информации о последовательности запуска переходов. Сложные АП-сети АП-сеть – это такая сложная сеть Петри, в которой каждый блок принадлежит к одному из 2-х типов: автоматному (А-блок) или блоку с параллелизмом (П-блок). Практическая часть.Задана сеть Петри, описывающая порядок выполнения операций в технологическом процессе. 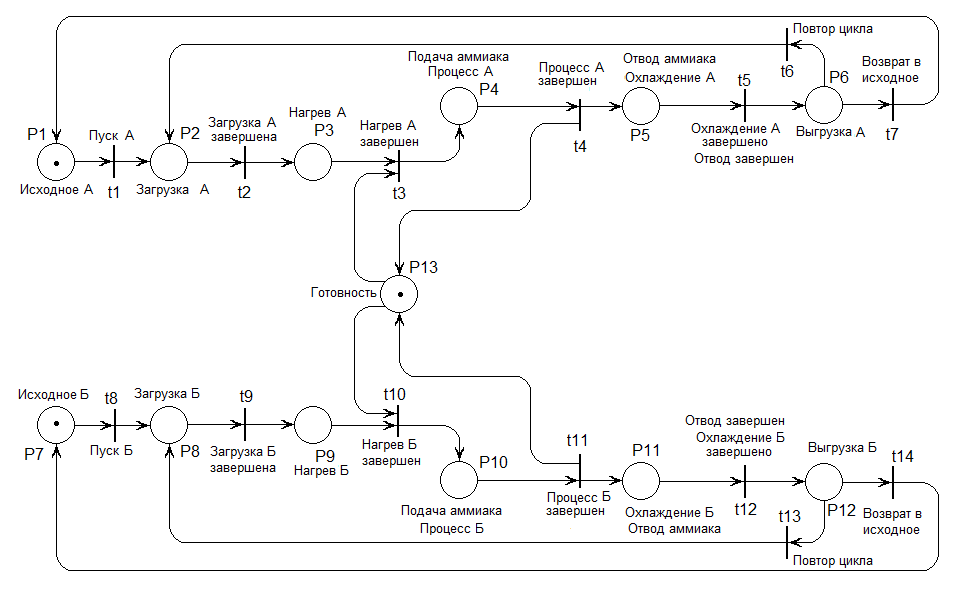 Рисунок 1. Сеть Петри для выполнения операции техпроцесса. Проанализировать сеть на безопасность и живость. Представить сеть в виде сложной АП-сети. Произвести анализ на безопасность и живость по старшей компоненте. Составить матричное уравнение для проверки достижимости маркировки (0,0,0,0,1,0,0,1,0,0,0,0,1). Составить операторные формулы для позиций р1, р5, р13. Выполнение. Для анализа сети на безопасность и живость составим древо достижимости для заданной сети. 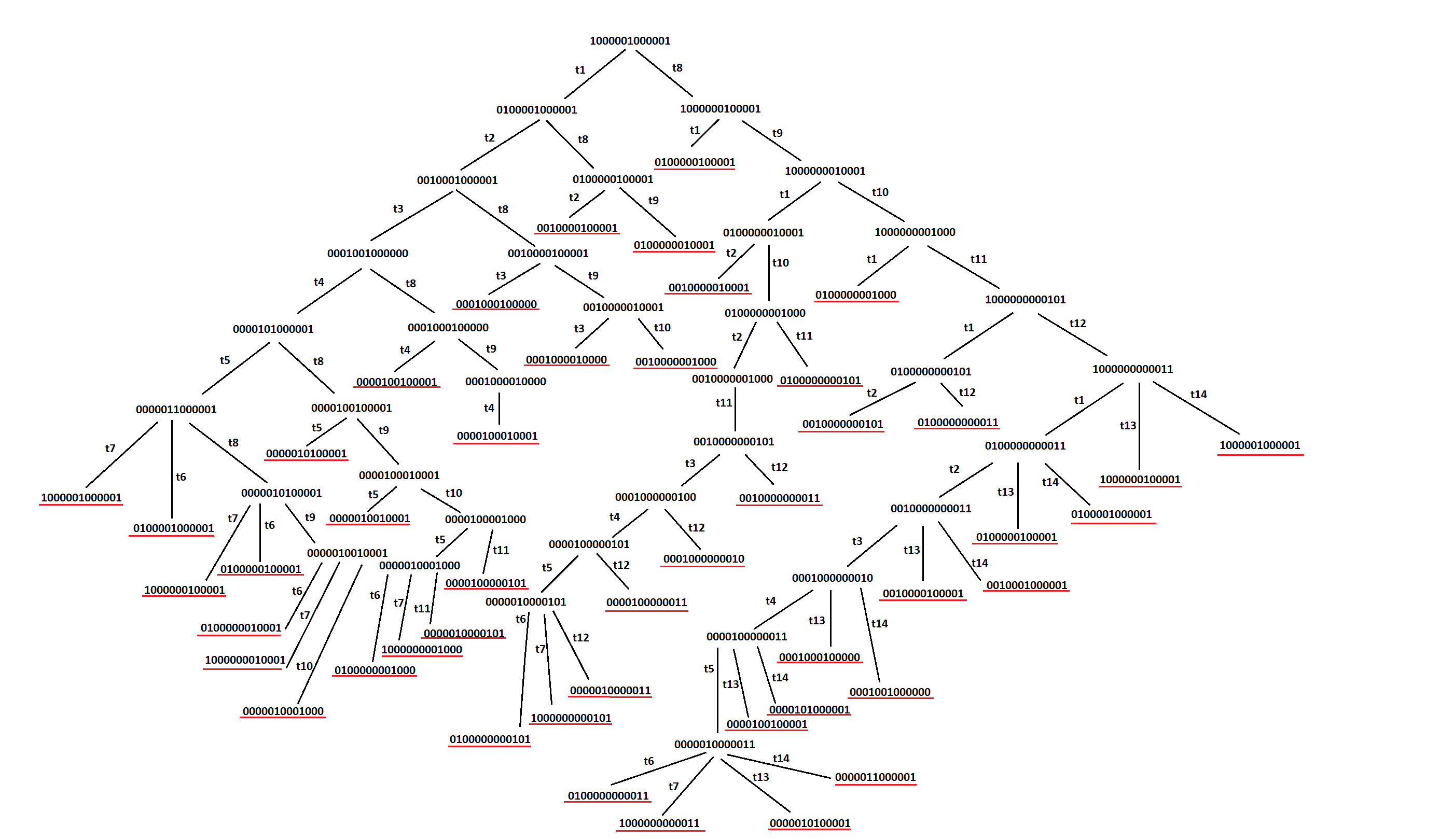 Рисунок 2. Древо достижимости. Проведем проверку безопасности Компоненты маркировок не превышают 1, следовательно можно считать, что сеть безопасна, так как не происходит накопления точек ни в одной из позиций. Проведем проверку живости Так как не существует тупиковых маркировок и все ветви древа ведут к дублирующим маркировкам, можно сделать вывод, что сеть является живой. Представим сеть в виде сложной АП-сети 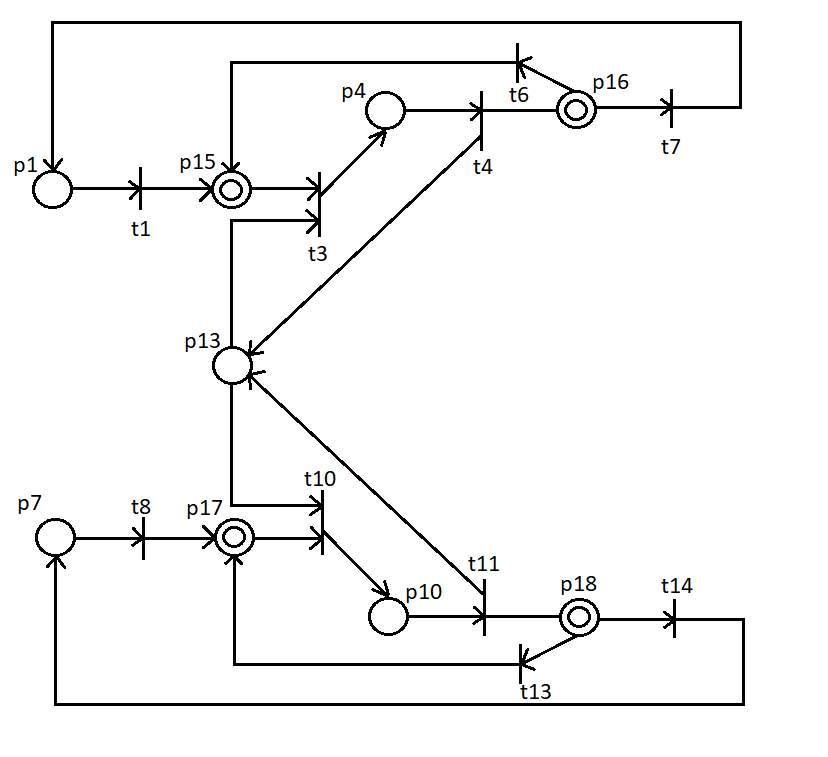 Рисунок 3. Сложная АП-сеть. p15 – А-блок 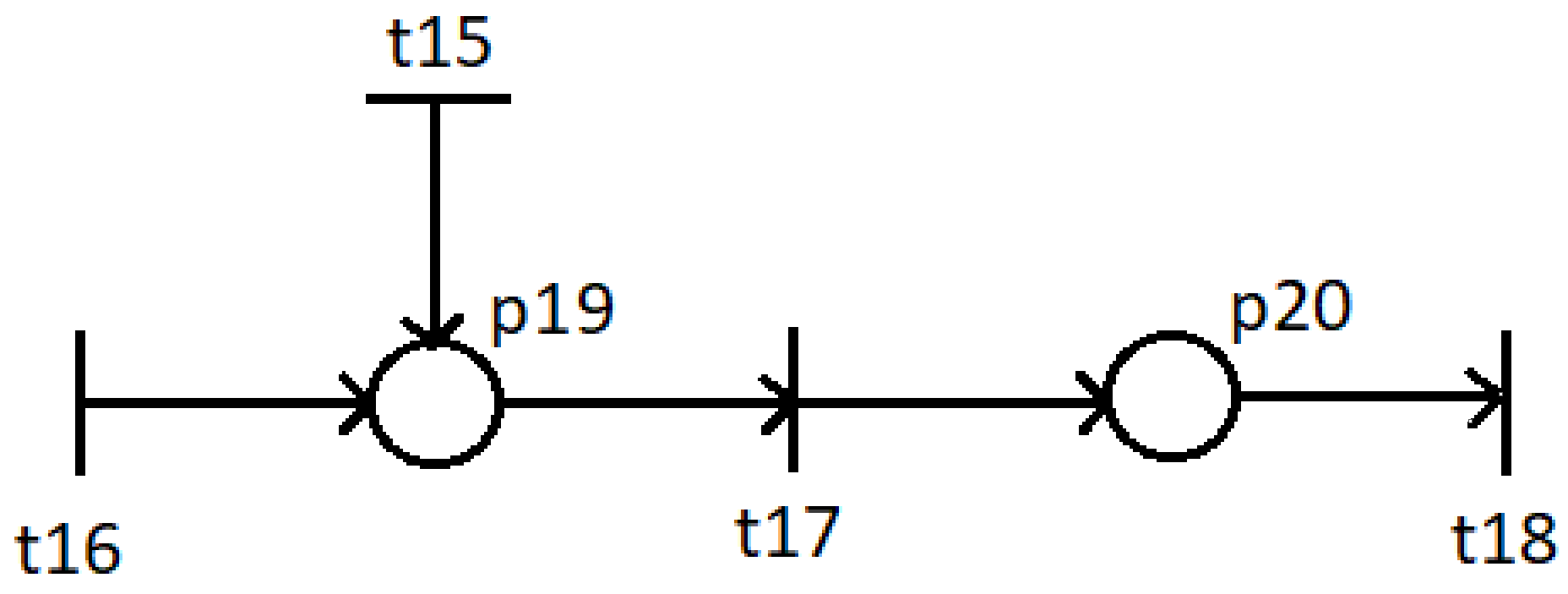 Рисунок 4. p15 – А-блок. p16 – А-блок 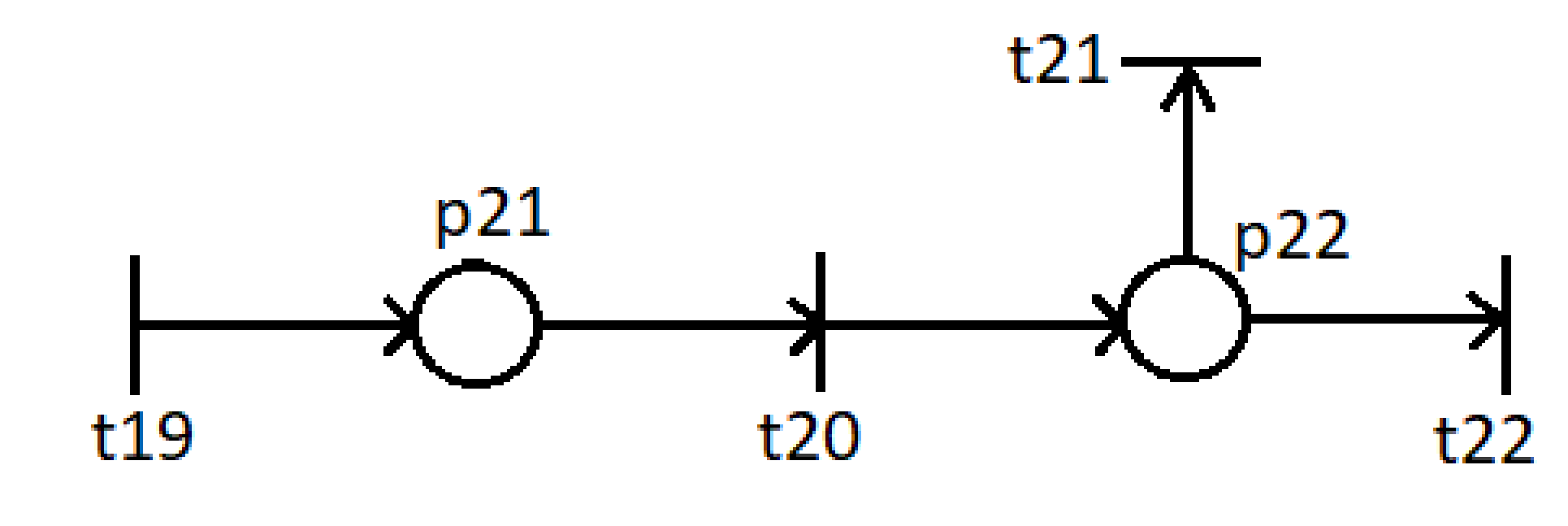 Рисунок 5. p16 – А-блок. p17 – А-блок 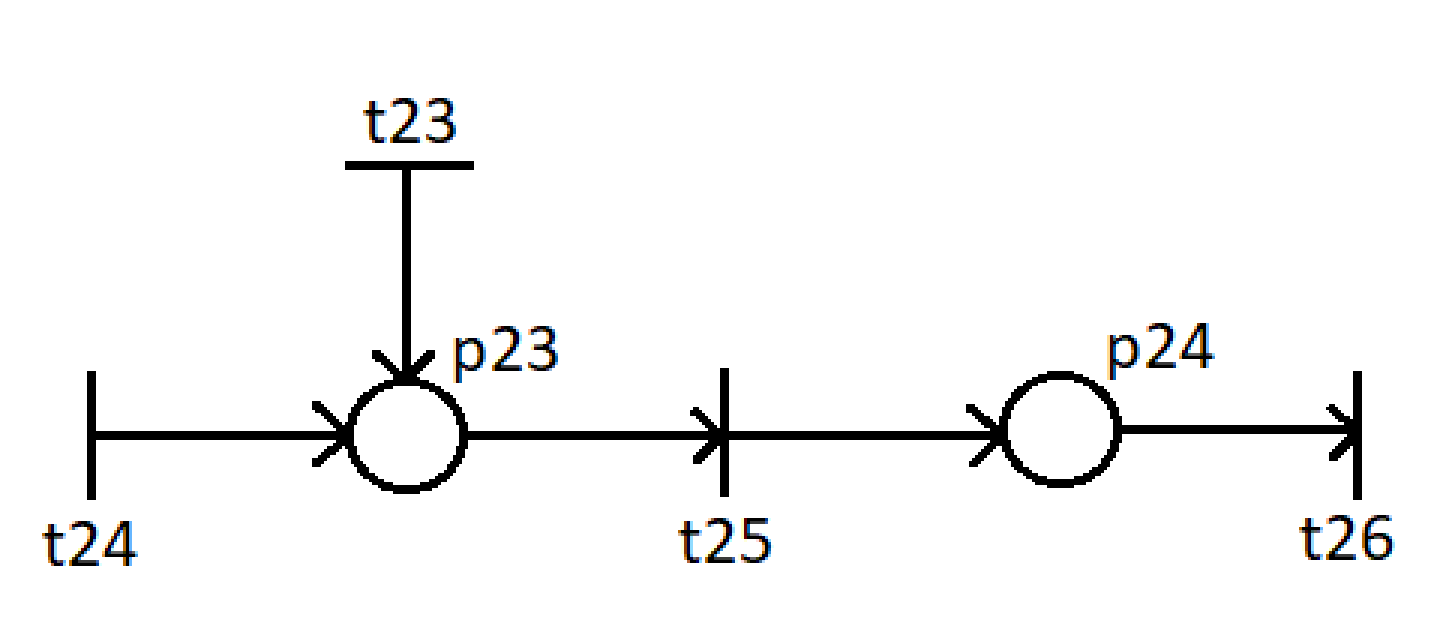 Рисунок 6. p17 – А-блок. p18 – А-блок 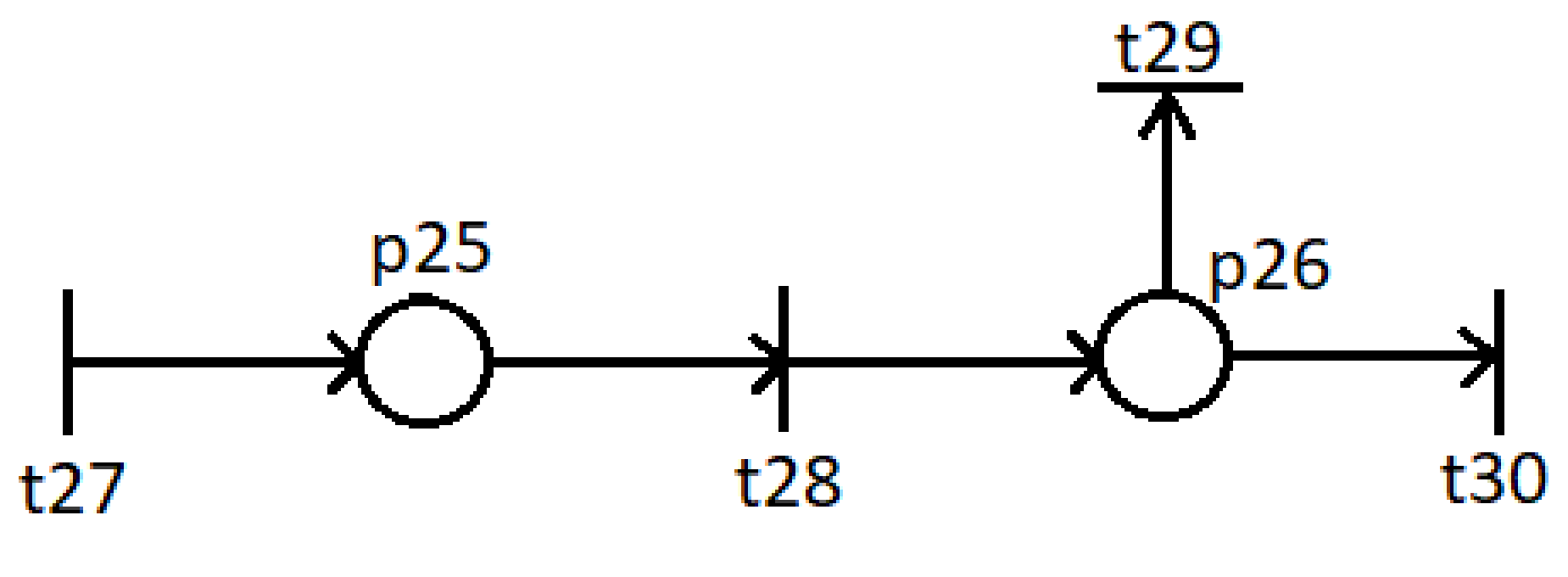 Рисунок 7. p18 – А-блок. Произведем анализ на безопасность и живость по старшей компоненте АП сеть безопасна, тогда и только тогда, когда безопасна её старшая компонента. АП сеть является живой, тогда и только тогда, когда её старшая компонента живая и в младших компонентах нет тупиковых стоков наборов относительно П-блоков.  Рисунок 8. Старшая компонента. Рисунок 8. Старшая компонента.Во всех позициях старшей компоненты количество точек в позиции никогда не превысит 1, следовательно вся АП-сеть безопасна. Для любой пары маркировок ( 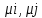 ), принадлежащих множеству ), принадлежащих множеству 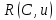 старшей компоненте сложной АП-сети, имеет место старшей компоненте сложной АП-сети, имеет место 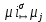 , следовательно вся АП-сеть живая. , следовательно вся АП-сеть живая.Составим матричное уравнение для проверки достижимости маркировки Строим матрицу входов D- P1 P2 P3 P4 P5 P6 P7 P8 P9 P10 P11 P12 P13 1 0 0 0 0 0 0 0 0 0 0 0 0 t1 0 1 0 0 0 0 0 0 0 0 0 0 0 t2 0 0 1 0 0 0 0 0 0 0 0 0 1 t3 0 0 0 1 0 0 0 0 0 0 0 0 0 t4 0 0 0 0 1 0 0 0 0 0 0 0 0 t5 0 0 0 0 0 1 0 0 0 0 0 0 0 t6 0 0 0 0 0 1 0 0 0 0 0 0 0 t7 0 0 0 0 0 0 1 0 0 0 0 0 0 t8 0 0 0 0 0 0 0 1 0 0 0 0 0 t9 0 0 0 0 0 0 0 0 1 0 0 0 1 t10 0 0 0 0 0 0 0 0 0 1 0 0 0 t11 0 0 0 0 0 0 0 0 0 0 1 0 0 t12 0 0 0 0 0 0 0 0 0 0 0 1 0 t13 0 0 0 0 0 0 0 0 0 0 0 1 0 t14 Строим матрицу выходов D + P1 P2 P3 P4 P5 P6 P7 P8 P9 P10 P11 P12 P13 0 1 0 0 0 0 0 0 0 0 0 0 0 t1 0 0 1 0 0 0 0 0 0 0 0 0 0 t2 0 0 0 1 0 0 0 0 0 0 0 0 0 t3 0 0 0 0 1 0 0 0 0 0 0 0 1 t4 0 0 0 0 0 1 0 0 0 0 0 0 0 t5 0 1 0 0 0 0 0 0 0 0 0 0 0 t6 1 0 0 0 0 0 0 0 0 0 0 0 0 t7 0 0 0 0 0 0 0 1 0 0 0 0 0 t8 0 0 0 0 0 0 0 0 1 0 0 0 0 t9 0 0 0 0 0 0 0 0 0 1 0 0 0 t10 0 0 0 0 0 0 0 0 0 0 1 0 1 t11 0 0 0 0 0 0 0 0 0 0 0 1 0 t12 0 0 0 0 0 0 0 1 0 0 0 0 0 t13 0 0 0 0 0 0 1 0 0 0 0 0 0 t14 Строим общую матрицу D = D+ - D- P1 P2 P3 P4 P5 P6 P7 P8 P9 P10 P11 P12 P13 -1 1 0 0 0 0 0 0 0 0 0 0 0 t1 0 -1 1 0 0 0 0 0 0 0 0 0 0 t2 0 0 1 1 0 0 0 0 0 0 0 0 -1 t3 0 0 0 -1 1 0 0 0 0 0 0 0 1 t4 0 0 0 0 -1 1 0 0 0 0 0 0 0 t5 0 1 0 0 0 -1 0 0 0 0 0 0 0 t6 1 0 0 0 0 -1 0 0 0 0 0 0 0 t7 0 0 0 0 0 0 -1 1 0 0 0 0 0 t8 0 0 0 0 0 0 0 -1 1 0 0 0 0 t9 0 0 0 0 0 0 0 0 -1 1 0 0 -1 t10 0 0 0 0 0 0 0 0 0 -1 1 0 1 t11 0 0 0 0 0 0 0 0 0 0 -1 1 0 t12 0 0 0 0 0 0 0 1 0 0 0 -1 0 t13 0 0 0 0 0 0 1 0 0 0 0 -1 0 t14 Составим матричное уравнение для проверки достижимости маркировки (0,0,0,0,1,0,0,1,0,0,0,0,1). Начальная маркировка (1,0,0,0,0,0,1,0,0,0,0,0,1). (0,0,0,0,1,0,0,1,0,0,0,0,1) = (1,0,0,0,0,0,1,0,0,0,0,0,1) + (x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12, x13, x14)*D (0,0,0,0,1,0,0,1,0,0,0,0,1) - (1,0,0,0,0,0,1,0,0,0,0,0,1) = (x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12, x13, x14)*D (-1,0,0,0,1,0,0,1,0,0,0,0,1) = (x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12, x13, x14)*D Получим систему уравнений: -x1 + x7 = -1 x1 - x2 + x6 = 0 x2 + x3 = 0 x3 - x4 = 0 x4 - x5 = 1 x5 - x6 - x7 = 0 -x8 + x14 = 0 x8 - x9 + x13=1 x9 - x10 = 0 x10 - x11 = 0 x11 - x12 = 0 x12 - x13 - x14 = 0 -x3 + x4 - x10 + x11 = 1 Так как количество уравнений 13, а количество неизвестных 14 – система не имеет однозначного решения, следовательно необходимое условие выполнено. Из древа достижимости мы видим, что достижение маркировки возможно при последовательном срабатывании переходов t1t2t3t8t4 или при t8t1t2t3t4 и других вариантах. Составим операторные формулы для позиций р1, р5, р13. Для позиции p1 p1 = T(x1p6; p2), где: x1 – сигнал с пульта оператора о возврате в исходное 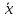 1 – сигнал с пульта оператора о повторе цикла. 1 – сигнал с пульта оператора о повторе цикла.Для позиции p5 p5 = T(x2p4; p6), где: x2 – сигнал о завершении процесса А Для позиции p13 p13 = T(x2p4˅x3p10; p4p10), где: x3 – сигнал о завершении процесса Б. Заключение:Мы проанализировали свойства сети Петри для двух параллельных процессов с разделяемым ресурсом. Составили древо достижимости маркировок, построили матричную систему уравнений для проверки достижимости маркировок, а также представили сеть в виде сложной АП-сети и составили операторные формулы для определенных позиций. Список литературы[1] Васильев, В.В. Сети Петри, параллельные алгоритмы и модели мультипроцессорных систем / В.В. Васильев, В.В. Кузьмук. - Киев: Наук. думка, 1990. - 216 с. [2] Никишечкин А. П., Букейханов Н.Б., Гвоздкова С. И., Барабошкин А. И. Сети Петри инструмент моделирования анализа и синтеза автоматизированных систем М.: ИЦ ГОУ МГТУ «СТАНКИН», 2006  242 с. 242 с.[3] Лазарев, В.Г. Синтез управляющих автоматов / В.Г. Лазарев, Е.И. Пийль. -М.: Энергоатомиздат, 1989. - 328 с. |
