курсач матан. Образовательное учреждение высшего профессионального образования воронежский государственный технический университет
 Скачать 413.66 Kb. Скачать 413.66 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» (ФГБОУ ВПО «ВГТУ», ВГТУ) Кафедра Систем информационной безопасности____________________ ЗАДАНИЕ на курсовую работу по дисциплине Математический анализ____________________________ __________________________________________________________________ Тема работы: Исследование SAIR-модели распространения вирусов Студент группы БТ-161 Ефимьева Юлия Игоревна _ Фамилия, имя, отчество Номер варианта ____________________________________________________ Технические условия ________________________________________________ __________________________________________________________________ Содержание и объем работы (графические работы, расчеты и прочее) Объем работы стр., рисунков – __________________________________________________________________ Сроки выполнения этапов ___________________________________________ Срок защиты курсовой работы ________________________________________ Руководитель доц. Е.Н. Провоторова Подпись, дата Инициалы, фамилия Задание принял студент Ю.И. Ефимьева Подпись, дата Инициалы, фамилия Замечания руководителя Содержание
Общая характеристика работы Актуальность Мы живем в 21 веке, во времена высоких информационных технологий. Информационная революция, начатая еще во второй половине двадцатого века, запустила механизм непрерывного развития информационных технологий, который все сильнее и сильнее набирает обороты, расширяя свой масштаб, свою значимость в жизни человека. По мнению историков, прогресс, который современное человечество достигает за год, равняется упорному десятилетнему труду ученых прошлого века. Современного человека, в отличие от его предков, повсюду окружают всевозможные высокотехнологические устройства, значительно упрощающие его жизнь, не оставляя ни одной сферы, в которой нельзя было бы их применить. С каждым годом появляются великое множество новых высокотехнологических устройств. Компьютерный рынок постоянно расширяется и предлагает нам новые или обновленные услуги, которые манят своей интеллектуальностью, заинтересовывая нас новыми возможностями, заставляя поверить во всемогущество искусственного интеллекта... Но не стоит сильно радоваться. Ведь все в этом мире находится в состоянии равновесия, а значит, появление новых благ неизбежно несет за собой и появление новых проблем. Информационные технологии, обрабатывающие наши данные беспрерывно подвергаются риску, что ставит перед нами серьезную задачу - обеспечить их безопасность. Самая мощная и серьезная угроза компьютерных пользователей - это вирусные атаки, которые беспощадно затрудняют важную работу с компьютерными данными. Поэтому необходимо принять все возможные меры, чтобы компьютерные системы были защищены. В рамках данной работы под компьютерным вирусом будем понимать программу, способную к самостоятельному поиску новых объектов для заражения и использующую для своего распространения разнообразные каналы связи. Существующие средства защиты не всегда оперативно справляются с эпидемиями компьютерных вирусов, поэтому становится актуальной задача создания систем обнаружения и защиты нового поколения, способных предотвратить или сдержать эпидемию на ранних стадиях. Для решения этой задачи необходимо уметь моделировать эпидемии с целью детального исследования этого феномена, анализа факторов, влияющих на распространение, и определения возможных механизмов обнаружения и противодействия. Одним из первых и важных этапов моделирования эпидемии компьютерных вирусов является выбор модели эпидемии, адекватно описывающей процесс их распространения. Мощным подходом для анализа распространения компьютерных вирусов является аналитическое моделирование. Преимуществом аналитического моделирования традиционно считается получение решения «в общем виде», а также высокая скорость моделирования конкретных сценариев для различных начальных условий. Кроме того, численные результаты, получаемые посредством таких моделей, позволяют анализировать поведение вирусов в сетях, состоящих из огромного числа элементов. Таким образом, аналитическое моделирование может использоваться для исследования вирусных эпидемий в сети Интернет. Сложность математического аппарата, используемого при аналитическом моделировании, связана со сложностью случайных процессов, происходящих при эпидемиях. К сложностям, с которыми приходится сталкиваться при аналитическом описании, относятся периоды бездействия в жизненном цикле вируса или его адаптивное поведение. Аналитический анализ распространения компьютерных вирусов уходит своими корнями к математическому описанию биологических процессов эпидемий. Математический аппарат для изучения динамики биологических эпидемий был разработан достаточно давно. Различные модели, заимствованные из эпидемиологии, уже применялись для моделирования динамики распространения Internet-червей. Биологический подход к моделированию вирусной проблемы по общему признанию начался с работ Д.Кефарта (J.Kephart) и С.Уайта (S.White) из IBM, однако модным это направление стало только в 2001 г., после вспышек эпидемий Code Red и Nimda. 1.2. Цели и задачи работы Целью данной курсовой работы является исследование аналитической модели эпидемии распространения вируса с использованием эпидемиологической SAIR-модели. Задачами работы являются: 1) изучение теории устойчивости; 2) исследование модели распространения вирусов на устойчивость; 3)поиск положений равновесия системы; Основное содержание 2.1. Описание модели SAIR Большинство моделей распространения вирусов представляют собой детерминированные модели эпидемий, то есть модели с фиксированными значениями параметров, оказывающих влияние на поведение системы в конкретных ситуациях. Такие модели подходят для моделирования эпидемии в той фазе, когда число инфицированных объектов достигло больших значений. В данной работе будет рассматриваться SAIR-модель, описывающая динамику распространения вирусов. В этой модели учитывается наличие антивирусного программного обеспечения. Все объекты в данной модели делятся на 4 типа: S (susceptible, что в переводе означает «восприимчивый») -неинфицированные объекты, восприимчивые к заражению; A (antidotal-«защищенный») - неинфицированные объекты, с установленным антивирусным программным обеспечением; I (infectious- «зараженный») -инфицированные объекты; R (removed, в переводе – «невосприимчивый») - «обезвреженные» объекты («вылеченные» антивирусом). В приводимых ниже формулах S(t), I(t), R(t) и A(t) обозначают количество соответствующих объектов. Графическое представление модели показано на рисунке 1. 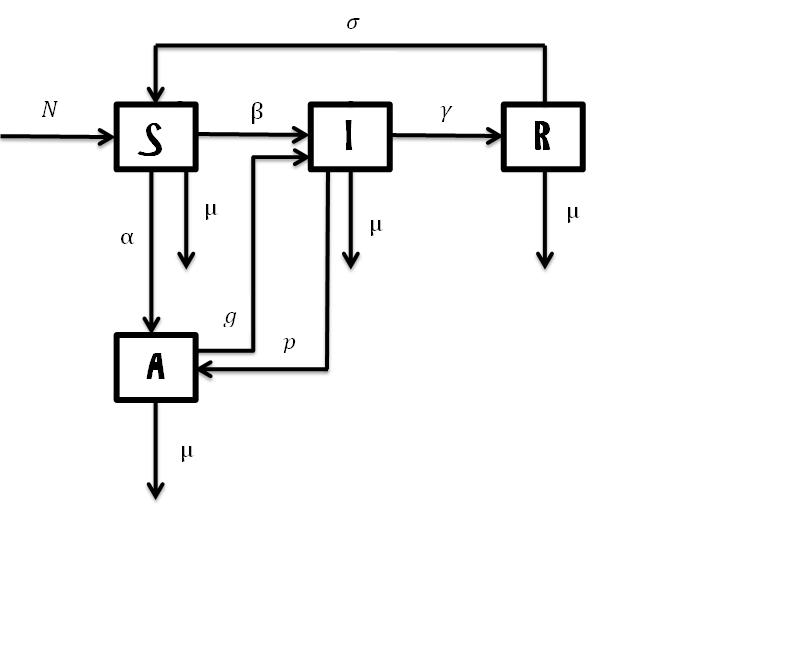 Рис.1. Схема SAIR-модели Как видно из рисунка, эта модель обладает множеством связей между объектами. Неинфицированный объект S может быть заражен вирусом. Это происходит вследствие наличия между восприимчивым S и зараженным I объектами связи. Так как эта модель имеет объект A, то при наличии связей между объектами I и A возможно восстановление инфицированных объектов или заражение объекта с антивирусным программным обеспечением, и при наличии связи между S и A возможен переход объекта из восприимчивого состояния в состояние защищенное. А также и другие переходы, показанные на схеме. Динамика данной SAIR-модели описывается следующими уравнениями: 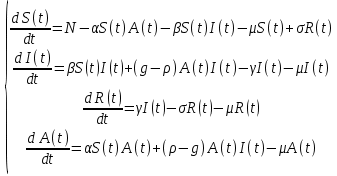 Параметры, используемые в рассматриваемой модели, описываются следующим образом: N- частота добавления новых объектов; 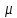 - коэффициент «смерти» объекта не из-за вируса; - коэффициент «смерти» объекта не из-за вируса;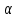 - коэффициент перехода объекта из восприимчивого состояния к состоянию с антивирусным программный обеспечением; - коэффициент перехода объекта из восприимчивого состояния к состоянию с антивирусным программный обеспечением; 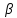 - коэффициент заражения восприимчивых объектов; - коэффициент заражения восприимчивых объектов;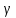 - коэффициент уничтожения зараженного объекта вирусом; - коэффициент уничтожения зараженного объекта вирусом;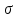 -коэффициент восстановления уничтоженных вирусом объектов; -коэффициент восстановления уничтоженных вирусом объектов;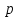 - коэффициент заражения вирусом защищенного объекта; - коэффициент заражения вирусом защищенного объекта; - коэффициент перехода зараженных узлов в состояние защищенности. - коэффициент перехода зараженных узлов в состояние защищенности.Все параметры, перечисленные выше, не зависят от времени протекания эпидемии, то есть являются константными значениями. 2.2. Понятие устойчивости решения дифференциальных уравнений и их систем 2.2.1. Понятие устойчивости по Ляпунову Рассмотрим нормальную систему дифференциальных уравнений: 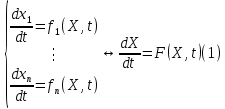 Пусть 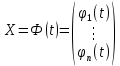 решение системы уравнений (1), соответствующие начальным условиям решение системы уравнений (1), соответствующие начальным условиям 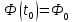 или или 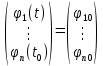 Кроме того, 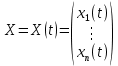 - решение системы уравнений (1), соответствующее измененным начальным условиям - решение системы уравнений (1), соответствующее измененным начальным условиям 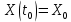 или или 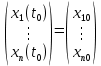 Определение. Решение системы (1) 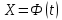 называется устойчивым по Ляпунову при называется устойчивым по Ляпунову при 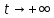 , если для любого , если для любого 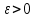 существует существует 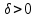 такое, что из совокупности неравенств такое, что из совокупности неравенств 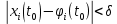 следуют неравенства следуют неравенства 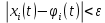 для любого для любого 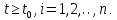 Из определения следует, что если 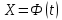 - устойчивое решение, то всякое решение, достаточно близкое к нему в начальный момент - устойчивое решение, то всякое решение, достаточно близкое к нему в начальный момент 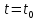 , остается близким к нему с ростом , остается близким к нему с ростом 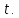 Иными словами решение 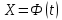 ( (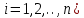 устойчиво, если достаточно близкое к нему в начальный момент устойчиво, если достаточно близкое к нему в начальный момент 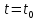 решение решение 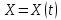 ( (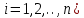 для всех для всех 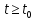 содержится в сколь угодно узкой содержится в сколь угодно узкой 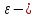 трубке, построенной вокруг решения трубке, построенной вокруг решения 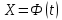 ( (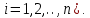 Это видно на рис. 2. Это видно на рис. 2.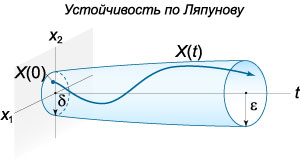 Рис.2 Если при сколь угодно малом 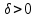 хотя бы для одного решения хотя бы для одного решения 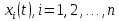 неравенства неравенства 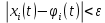 не выполняются, то решение не выполняются, то решение 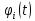 называется неустойчивым. называется неустойчивым.Определение. Решение системы (1) 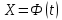 называется асимптотически устойчивым по Ляпунову, если существует называется асимптотически устойчивым по Ляпунову, если существует 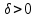 такое, что из совокупности неравенств такое, что из совокупности неравенств 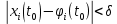 следует, что следует, что 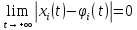 , , 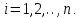 Из определения следует, что всякое решение, достаточно близкое к X 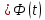 в начальный момент в начальный момент 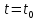 , неограниченно сближается с ним с ростом , неограниченно сближается с ним с ростом 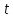 . .Определение. Решение системы (1) 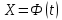 называется асимптотически устойчивым в целом, если называется асимптотически устойчивым в целом, если 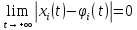 , , где 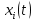 - решение, определяемое любыми начальными условиями, а не только значениями, близкими к начальным значениям - решение, определяемое любыми начальными условиями, а не только значениями, близкими к начальным значениям 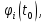 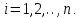 Рассмотрим систему уравнений (1). Каждому решению системы соответствует интегральная кривая 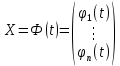 , или траектория. Если эта система имеет не зависящее от , или траектория. Если эта система имеет не зависящее от 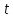 решение решение 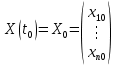 , , 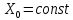 , то соответствующая траектория будет точкой. Она называется точкой покоя системы (1), или ее положением равновесия. В частности, тривиальное решение , то соответствующая траектория будет точкой. Она называется точкой покоя системы (1), или ее положением равновесия. В частности, тривиальное решение 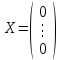 называется точкой покоя этой системы, расположенной в начале координат. называется точкой покоя этой системы, расположенной в начале координат.Она существует, если 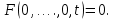 Определение. Тривиальное решение системы (1) называется устойчивым по Ляпунову, если для любого 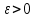 существует существует 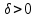 такое, что из совокупности неравенств такое, что из совокупности неравенств 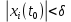 следуют неравенства следуют неравенства 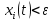 для любого для любого 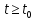 , , 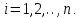 Этому определению можно дать другую, эквивалентную формулировку. Определение. Точка покоя, расположенная в начале координат, называется устойчивой по Ляпунову, если для любого 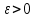 существует существует 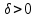 такое, что из совокупности неравенства такое, что из совокупности неравенства 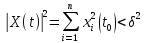 следует, что следует, что 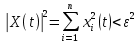 для любого для любого 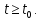 Геометрически это означает, что если тривиальное решение устойчиво, то всякая траектория, определяемая начальной точкой 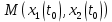 и начинающая внутри круга (сферы) радиуса и начинающая внутри круга (сферы) радиуса 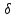 , не покидает при , не покидает при 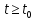 круга (сферы) радиуса круга (сферы) радиуса 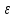 (рис.3) с центром в начале координат. (рис.3) с центром в начале координат.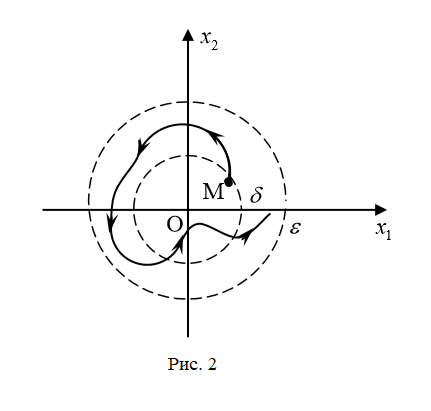 Рис.3 Определение. Тривиальное решение системы (1) называется асимптотически устойчивым, если существует 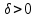 такое, что из совокупности неравенств такое, что из совокупности неравенств 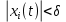 следует, что следует, что 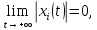 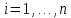 , или, другими словами, если из неравенства , или, другими словами, если из неравенства 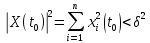 следует, что следует, что 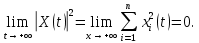 Геометрическая иллюстрация этого определения показана на рис.4. Если тривиальное решение асимптотически устойчиво, то любая траектория, которая определяется начальной точкой 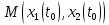 в круге радиуса в круге радиуса 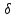 , не только не выйдет из этого круга, но и будет стремиться к его центру , не только не выйдет из этого круга, но и будет стремиться к его центру 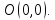 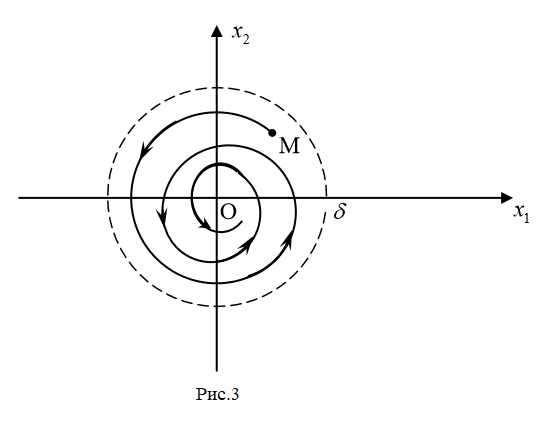 Рис.4 Исследование на устойчивость любого частного решения системы (1) можно заменить исследованием устойчивости тривиального решения некоторой другой системы. Рассмотрим это. Пусть 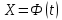 - исследуемое решение. Введем новую переменную - исследуемое решение. Введем новую переменную 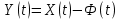 . Если решение . Если решение 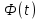 устойчиво, то любое решение устойчиво, то любое решение 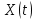 , близкое к нему в начальный момент , близкое к нему в начальный момент 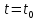 , остается близким к нему и при , остается близким к нему и при 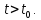 Отсюда следует, что если при Отсюда следует, что если при 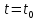 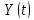 близко к началу координат, то близко к началу координат, то 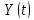 не удаляется от не удаляется от 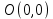 и с увеличением и с увеличением 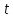 . .Выясним, какой системе уравнений удовлетворяет функция 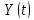 , если , если 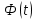 удовлетворяет (1): удовлетворяет (1):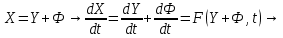 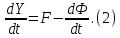 Система (2) имеет тривиальное решение 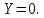 Если оно устойчиво, то устойчиво любое частное решение системы (1). Если оно устойчиво, то устойчиво любое частное решение системы (1).Рассмотрим неоднородную систему 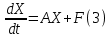 и соответствующую ей однородную систему линейных дифференциальных уравнений 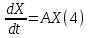 Исследуем на устойчивость частное решение системы (3) 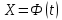 . Пусть . Пусть 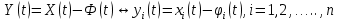 – это отклонение точек на произвольной траектории – это отклонение точек на произвольной траектории 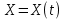 соответствующих точек исследуемой траектории соответствующих точек исследуемой траектории 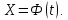 Такое отклонение называется возмущением. Такое отклонение называется возмущением.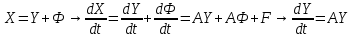 , так как , так как 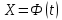 удовлетворяет (3). удовлетворяет (3).Таким образом, если решение 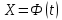 неоднородной системы (3) устойчиво, то устойчиво и тривиальное решение соответствующей однородной системы (4) и, наоборот: из устойчивости нулевого решения однородной системы (4) следует устойчивость решения неоднородной системы (3) устойчиво, то устойчиво и тривиальное решение соответствующей однородной системы (4) и, наоборот: из устойчивости нулевого решения однородной системы (4) следует устойчивость решения 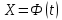 неоднородной системы (3). неоднородной системы (3).Итак, все частные решения неоднородной системы (3) в смысле устойчивости ведут себя так же, как и тривиальное решение соответствующей однородной системы (4). Поэтому исследование устойчивости произвольного решения системы (3) можно заменить исследованием устойчивости точки покоя, расположенной в начале координат, однородной системы (4). Пример 1. Пользуясь определением устойчивости по Ляпунову, исследовать на устойчивость решение следующего уравнения системы: 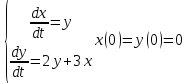 Решение: Сначала найдем общее решение системы, используя метод исключения. В результате решение имеет следующий вид: 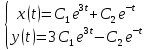 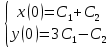 Найдем значение 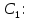 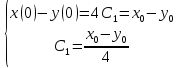 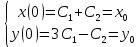 Найдем значение 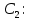 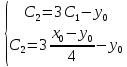 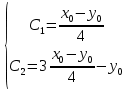 Тогда следующая система является искомым частным решением 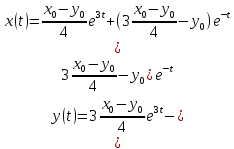 Выполним некоторые преобразования в системе. Множитель 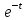 стремится к нулю при стремится к нулю при 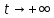 , следовательно, упростим следующие выражения: , следовательно, упростим следующие выражения: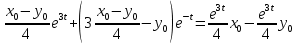 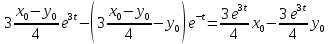 Следовательно, система примет вид: 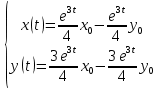 Отсюда 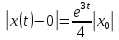 + +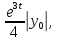 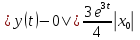 + +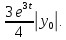 При 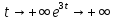 , поэтому какими бы близкими к нулю ни были бы значения , поэтому какими бы близкими к нулю ни были бы значения 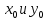 , , 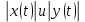 неограниченно возрастают, то есть найденные решения неограниченно удаляются от решений неограниченно возрастают, то есть найденные решения неограниченно удаляются от решений 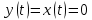 . По определению означает, что тривиальное решение является неустойчивым. . По определению означает, что тривиальное решение является неустойчивым. Ответ: решение неустойчивое. 2.2.2. Простейшие типы точек покоя Рассмотрим, линейную однородную систему 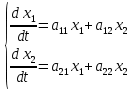 , ,где 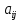 -числа и -числа и 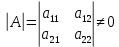 . Это автономная система. Вид ее решение зависит от характеристических корней матрицы A. Изучив все возможные случаи решений, мы получим следующие расположения траекторий в окрестности точки покоя . Это автономная система. Вид ее решение зависит от характеристических корней матрицы A. Изучив все возможные случаи решений, мы получим следующие расположения траекторий в окрестности точки покоя 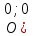 ): ):Если 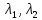 -действительные числа, -действительные числа, 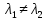 , , 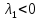 , , 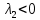 , то точка покоя асимптотически устойчива. Точку покоя при таком расположении траекторий называют устойчивым узлом. (Рис. 5) , то точка покоя асимптотически устойчива. Точку покоя при таком расположении траекторий называют устойчивым узлом. (Рис. 5)Если 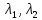 -действительные числа, -действительные числа, 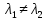 , , 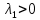 , , 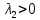 , то точка покоя неустойчива. Её называют неустойчивым узлом. (Рис. 6) , то точка покоя неустойчива. Её называют неустойчивым узлом. (Рис. 6)Если 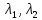 -действительные числа, -действительные числа, 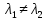 , , 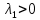 , , 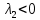 , то точка покоя неустойчива. Её называют седлом. (Рис. 7) , то точка покоя неустойчива. Её называют седлом. (Рис. 7)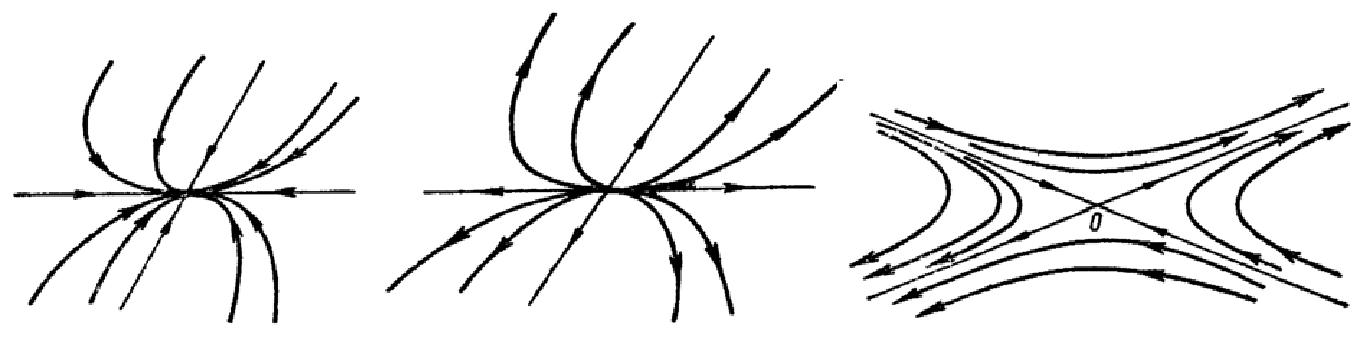 Рис. 5 Рис. 6 Рис.7    Если 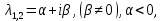 то точка покоя асимптотически устойчива. Её называют устойчивым фокусом. (Рис. 8) то точка покоя асимптотически устойчива. Её называют устойчивым фокусом. (Рис. 8)Если 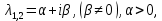 то точка покоя неустойчива. Её называют неустойчивым фокусом. (Рис. 9) то точка покоя неустойчива. Её называют неустойчивым фокусом. (Рис. 9)Если 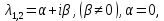 то точка покоя устойчива. Её называют центром. (Рис. 10) то точка покоя устойчива. Её называют центром. (Рис. 10) Рис. 8 Рис. 9 Рис.10 Если 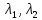 -действительные числа, -действительные числа, 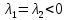 , то точка покоя асимптотически устойчива. При таком расположении, как на рисунке 11, ее называют устойчивым вырожденным узлом. Если траектории располагаются, как на рисунке 12, то устойчивым диакритическим узлом. , то точка покоя асимптотически устойчива. При таком расположении, как на рисунке 11, ее называют устойчивым вырожденным узлом. Если траектории располагаются, как на рисунке 12, то устойчивым диакритическим узлом.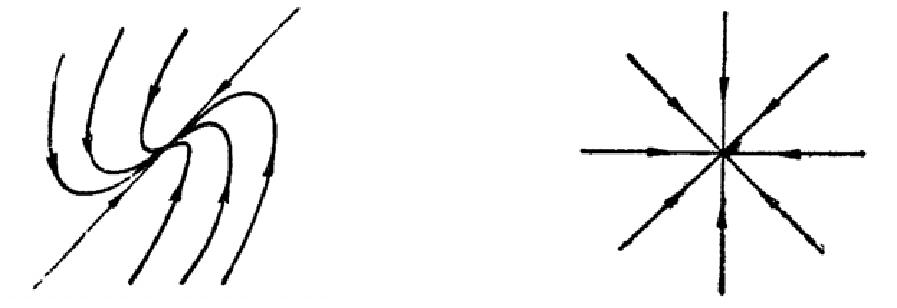 Рис.11 Рис.12 Если 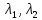 -действительные числа, -действительные числа, 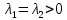 , то точка покоя неустойчива. Её называют неустойчивым вырожденным узлом или неустойчивым диакритическим узлом. (Рис. 13 и 14) , то точка покоя неустойчива. Её называют неустойчивым вырожденным узлом или неустойчивым диакритическим узлом. (Рис. 13 и 14)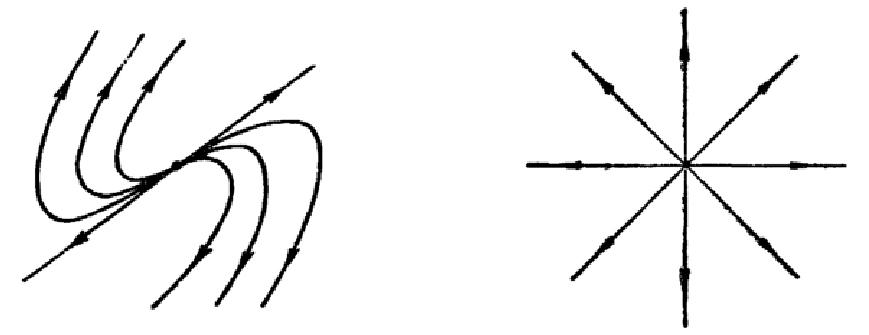 Рис. 13 Рис. 14 Пример 2. Установить характер точки покоя (0;0) в следующей системе: 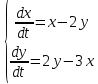 Решение: В данном случае коэффициенты равны 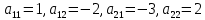 . .Составим характеристическое уравнение 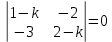 или 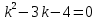 . .Корни этого уравнения равны 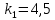 , , 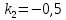 . Они оба действительные, один из них меньше нуля, другой больше, следовательно, точка покоя неустойчива (седло). То есть получается такое примерное расположение траекторий: . Они оба действительные, один из них меньше нуля, другой больше, следовательно, точка покоя неустойчива (седло). То есть получается такое примерное расположение траекторий: Ответ: точка покоя неустойчива (седло). 2.2.3. Устойчивость по первому приближению Нормальная система дифференциальных уравнений называется автономной, если ее правые части 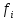 не зависят явно от t, то есть если она имеет вид не зависят явно от t, то есть если она имеет вид 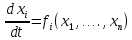 , , 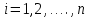 . .Рассмотрим автономную систему дифференциальных уравнений 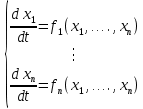 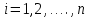 (5) (5)Пусть система (5) имеет тривиальное решение, то есть 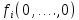 для любого для любого 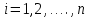 . И все функции . И все функции 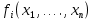 дифференцируемы в некоторой окрестности начала координат. дифференцируемы в некоторой окрестности начала координат.В этой окрестности по определению дифференцируемой функции нескольких переменных 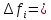 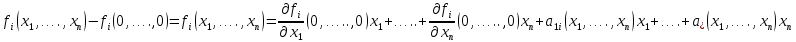 , где , где 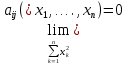 для любого для любого 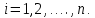 Поэтому вблизи начала координат слагаемые 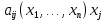 имеют более высокий порядок малости, чем линейные слагаемые имеют более высокий порядок малости, чем линейные слагаемые 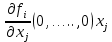 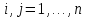 . .В некоторых случаях при исследовании устойчивости тривиального решения системы (5) нелинейными слагаемыми правой части можно пренебречь, считая, что 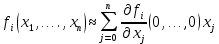 . .Тогда систему дифференциальных уравнений (5) можно заменить близкой ей системой при достаточно малых 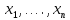 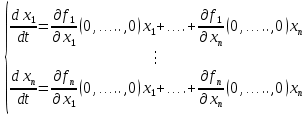 Обозначим 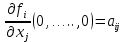 и вместо системы (5) рассмотрим линейную однородную систему с постоянными коэффициентами и вместо системы (5) рассмотрим линейную однородную систему с постоянными коэффициентами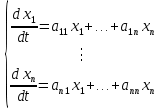 (6) (6)Линейная однородная система (6) называется системой первого приближения системы (5). Замена исследования устойчивости тривиального решения системы (5) исследованием устойчивости тривиального решения системы (6) называется исследованием устойчивости решения системы (5) по первому приближению. Справедливы следующие предложения: Если все корни характеристического уравнения 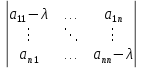 =0 (7) =0 (7)имеют отрицательные вещественные части, то нулевое решение системы (3) и системы (2) асимптотически устойчиво. Если хотя бы один корень характеристического уравнения (7) имеет положительную вещественную часть, то нулевое решения системы (3) и системы (2) неустойчиво. Говорят, что в случаях 1 и 2 исследование на устойчивость по первому приближению возможно. В критических случаях, когда вещественные части всех корней характеристического уравнения (7) неположительные, причем вещественная часть хотя бы одного корня равна нулю, исследование по первому приближению не возможно, потому что начинают влиять нелинейные слагаемые, которые отбрасываются при составлении системы первого приближения. Пример 3. Исследовать на устойчивость по первому приближению точку покоя 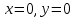 в следующей системе: в следующей системе: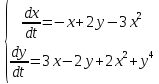 Решение: При 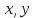 достаточно близких к нулю слагаемые достаточно близких к нулю слагаемые 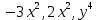 имеют достаточно высокий порядок малости, чем имеют достаточно высокий порядок малости, чем 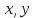 , поэтому ими можно пренебречь при составлении системы первого приближения. , поэтому ими можно пренебречь при составлении системы первого приближения.Составим систему первого приближения, отбросив нелинейные слагаемые. Следовательно, система примет вид: 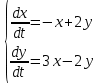 Характеристическое уравнение 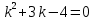 имеет такие корни: имеет такие корни: 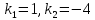 , поэтому для системы первого приближения и первоначальной системы точка покоя является неустойчивой. , поэтому для системы первого приближения и первоначальной системы точка покоя является неустойчивой.Ответ: точка покоя неустойчива. Метод функций Ляпунова Метод функций Ляпунова позволяет исследовать устойчивость решений систем дифференциальных уравнений с помощью специально построенных функций, так называемых функций Ляпунова, не находя самих решений. Рассмотрим неавтономную систему дифференциальных уравнений (1): 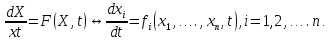 Пусть эта система имеет тривиальное решение, то есть 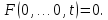 Как было показано раньше все решения системы в смысле устойчивости ведут себя так же, как тривиальное решение. Как было показано раньше все решения системы в смысле устойчивости ведут себя так же, как тривиальное решение.Пусть 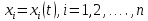 - некоторое решение системы (1), которое определяет соответствующую ему траекторию. - некоторое решение системы (1), которое определяет соответствующую ему траекторию. 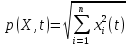 - расстояние от точек на этой траектории до начала координат. Найдем его полную производную по времени (рис. 4): - расстояние от точек на этой траектории до начала координат. Найдем его полную производную по времени (рис. 4):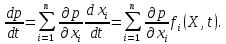 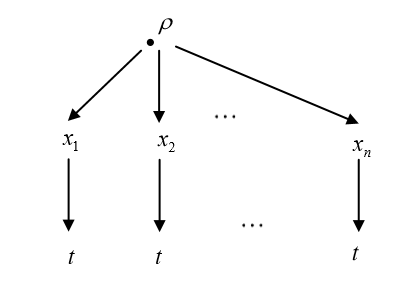 Рис. 15 Заметим, что даже если сама траектория неизвестна, то найденная производная есть известная функция. Если 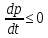 , то расстояние от точек на траектории до начала координат не увеличивается, то есть все траектории, определяемые частными решениями, близкими к , то расстояние от точек на траектории до начала координат не увеличивается, то есть все траектории, определяемые частными решениями, близкими к 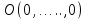 в начальный момент, остаются близкими к началу координат с ростом в начальный момент, остаются близкими к началу координат с ростом 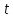 . Это по определению означает, что тривиальное решение устойчиво. . Это по определению означает, что тривиальное решение устойчиво.Если 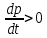 , то расстояние с ростом , то расстояние с ростом 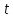 увеличивается, следовательно, нулевое решение неустойчиво. увеличивается, следовательно, нулевое решение неустойчиво.Функция 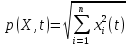 в этих рассуждениях может быть заменена на более удобную в вычислениях функцию в этих рассуждениях может быть заменена на более удобную в вычислениях функцию 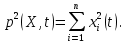 Определение. Производной функции 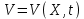 в силу системы (1) называется производная в силу системы (1) называется производная 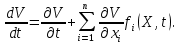 Рассмотрим автономную систему дифференциальных уравнений 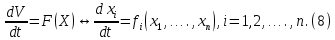 Будем считать, что для такой системы функция 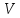 не зависит от времени и ее производная в силу системы (8) имеет вид: не зависит от времени и ее производная в силу системы (8) имеет вид: 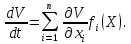 Определение. Функция 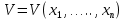 называется положительно (отрицательно) определенной в некоторой называется положительно (отрицательно) определенной в некоторой 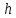 -окрестности начала координат, если всюду в этой окрестности -окрестности начала координат, если всюду в этой окрестности 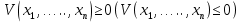 и только и только 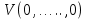 =0. =0. Положительно или отрицательно определенные функции называются знакоопределенными. Напомним, что 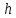 -окрестностью начала координат называется множество точек, определяемое неравенством -окрестностью начала координат называется множество точек, определяемое неравенством 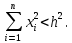 Если Если 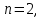 то это круг радиуса то это круг радиуса 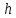 с центром в начале координат; если с центром в начале координат; если 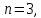 то это шар радиуса то это шар радиуса 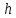 . .Определение. Функция V 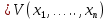 называется неотрицательной (неположительной) в некоторой называется неотрицательной (неположительной) в некоторой 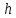 -окрестности начала координат, если всюду в этой окрестности -окрестности начала координат, если всюду в этой окрестности 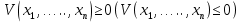 , причем , причем 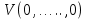 =0 не только при =0 не только при 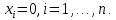 Неотрицательные и неположительные функции называются знакопостоянными. Определение. Функция 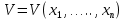 называется функцией Ляпунова автономной системы (8), если называется функцией Ляпунова автономной системы (8), еслифункция 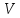 дифференцируема в некоторой окрестности начала координат; дифференцируема в некоторой окрестности начала координат;функция 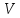 положительно определена (отрицательно определена) в этой окрестности; положительно определена (отрицательно определена) в этой окрестности;ее производная в силу системы (8) 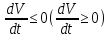 всюду в этой окрестности. всюду в этой окрестности.Рассмотрим систему (8) и будем считать, что она имеет тривиальное решение 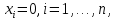 то есть то есть 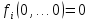 для любого для любого 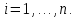 Теорема Ляпунова об устойчивости. Пусть существует дифференцируемая функция 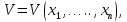 знакоопределенная в некоторой окрестности начала координат, производная которой в силу системы (8) знакопостоянна в этой окрестности и противоположного с знакоопределенная в некоторой окрестности начала координат, производная которой в силу системы (8) знакопостоянна в этой окрестности и противоположного с 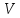 знака или тождественно равная нулю. Тогда тривиальное решение системы (8) устойчиво. знака или тождественно равная нулю. Тогда тривиальное решение системы (8) устойчиво.Доказательство. Пусть функция 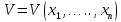 дифференцируема и положительно определена в некоторой дифференцируема и положительно определена в некоторой 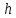 -окрестности начала координат, а ее производная в силу системы (8) -окрестности начала координат, а ее производная в силу системы (8) 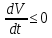 или или 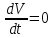 . Зададим . Зададим 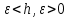 и пусть и пусть 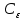 -граница -граница 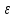 -окрестности начала координат (рис. 16). Из дифференцируемости -окрестности начала координат (рис. 16). Из дифференцируемости 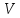 следует ее непрерывность как внутри -окрестности, так и на ее границе следует ее непрерывность как внутри -окрестности, так и на ее границе 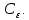 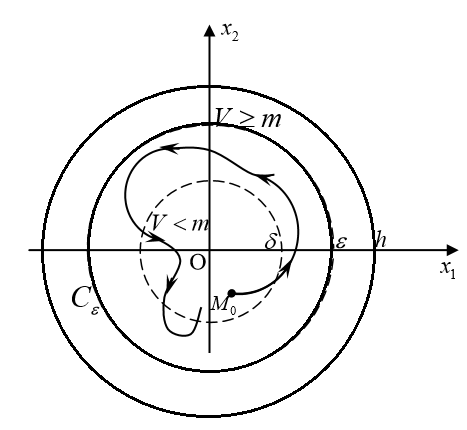 Рис. 16 Граница 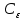 -ограниченное и замкнутое множество, поэтому непрерывная функция -ограниченное и замкнутое множество, поэтому непрерывная функция 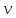 достигает на ней своих наибольшего и наименьшего значений. Обозначим -наименьшее значение достигает на ней своих наибольшего и наименьшего значений. Обозначим -наименьшее значение 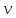 на на 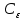 . Отметим, что, так как . Отметим, что, так как 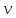 положительна определена, то положительна определена, то 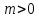 . Функция . Функция 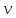 непрерывна в -окрестности начала координат, непрерывна в -окрестности начала координат, 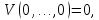 а на а на 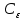 имеет место неравенство имеет место неравенство 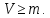 Поэтому существует такая Поэтому существует такая 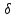 -окрестность ( -окрестность (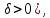 во всех точках которой во всех точках которой 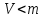 . .Пусть 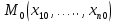 - произвольная точка этой - произвольная точка этой 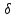 –окрестности. –окрестности.Начальные условия 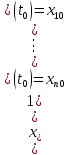 определяют некоторое решение системы (8). Соответствующая траектория начинается в точке определяют некоторое решение системы (8). Соответствующая траектория начинается в точке 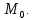 При движении вдоль этой траектории функция При движении вдоль этой траектории функция 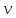 не убывает, так как по условию не убывает, так как по условию 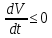 или или 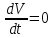 , поэтому , поэтому 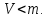 Это означает, что траектория не выйдет за пределы -окрестности, так как в противном случае она пересечет границу Это означает, что траектория не выйдет за пределы -окрестности, так как в противном случае она пересечет границу 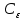 , на которой , на которой 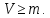 Таким образом, по определению почка покоя системы (8) устойчива. Теорема Ляпунова об асимптотической устойчивости. Пусть в некоторой 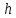 -окрестности начала координат существует дифференцируемая функция -окрестности начала координат существует дифференцируемая функция 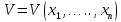 , положительно определенная в этой окрестности, производная в силу системы которой отрицательно определена. Тогда тривиальное решение системы (8) асимптотически устойчиво. , положительно определенная в этой окрестности, производная в силу системы которой отрицательно определена. Тогда тривиальное решение системы (8) асимптотически устойчиво.Метод функций Ляпунова универсален и эффективен, но недостаток его в том, что не существует конструктивного алгоритма построения функций Ляпунова для произвольной системы дифференциальных уравнений. В простейших случаях можно искать функцию Ляпунова в виде 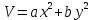 , , 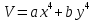 , , 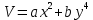 и так далее. и так далее.Пример 4. Исследовать на устойчивость тривиальное решение системы: 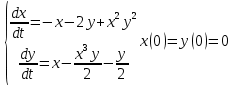 Решение: Будем искать функцию Ляпунова в следующем виде: 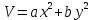 , где , где 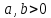 – произвольные параметры. – произвольные параметры.Имеем 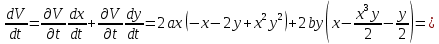 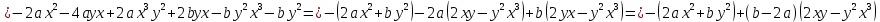 Примем 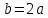 , получим, что , получим, что 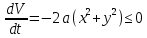 . Таким образом, при всяком . Таким образом, при всяком 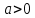 и и 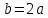 функция функция 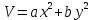 будет определенно-положительной, а ее производная будет определенно-положительной, а ее производная 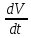 , составленная в силу данной системы, является-отрицательной. Из теоремы Ляпунова следует, что тривиальное решение данной системы асимптотически устойчиво. , составленная в силу данной системы, является-отрицательной. Из теоремы Ляпунова следует, что тривиальное решение данной системы асимптотически устойчиво.Ответ: асимптотически устойчиво. Исследование системы дифференциальных уравнений, описывающей SAIR-модель Рассмотрим исходную систему дифференциальных уравнений, характеризующую SAIR-модель. Для простоты анализа частоту добавления новых объектов полагают равной нулю ( 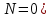 , подразумевая, что во время развития эпидемии не происходит добавление новых объектов. По этой же причине примем коэффициент смертности объектов, не связанной с вирусом, равным нулю ( , подразумевая, что во время развития эпидемии не происходит добавление новых объектов. По этой же причине примем коэффициент смертности объектов, не связанной с вирусом, равным нулю (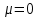 ). С учетом этих допущений моделируемая система описывается следующей системой уравнений (9): ). С учетом этих допущений моделируемая система описывается следующей системой уравнений (9):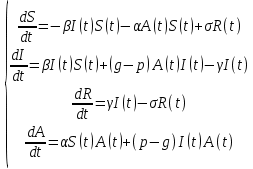 Так как 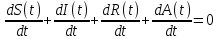 , ,то 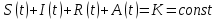 для любых для любых 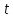 . .Положение равновесия системы в условиях отсутствия вирусов Чтобы исследовать динамику модели введем точки равновесия, считая все производные функций, отображающие количество узлов в блоках S, A, I, R, равными нулю в таких точках (если они существуют). 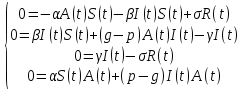 Для начала рассмотрим систему без распространения в ней вируса. То есть ситуацию, при которой отсутствует заражение в системе ( 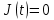 ).Учитывая, что ).Учитывая, что 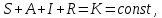 она характеризуется следующими начальными условиями: она характеризуется следующими начальными условиями: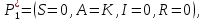 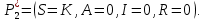 Таким образом, все объекты либо уязвимы, либо неуязвимы при 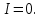 Запишем для каждой из выбранных точек характеристическое уравнение, соответствующее данной системе уравнений, и найдем его корни. Для точки 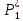 характеристическое уравнение выглядит следующим образом: характеристическое уравнение выглядит следующим образом: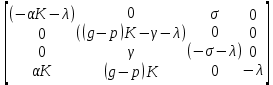 В результате решения этого уравнения получились следующие корни: 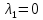 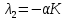 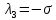 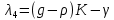 Получившееся нулевое значение 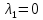 говорит лишь о том, что одно из уравнений системы можно представить в виде линейной комбинации остальных. Корень говорит лишь о том, что одно из уравнений системы можно представить в виде линейной комбинации остальных. Корень 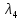 может принимать любые значения. Но чтобы значение удовлетворяло теореме об устойчивости точки (т.е. было действительным и отрицательным), необходимо выполнение следующего условия: может принимать любые значения. Но чтобы значение удовлетворяло теореме об устойчивости точки (т.е. было действительным и отрицательным), необходимо выполнение следующего условия: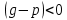 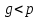 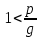 Остальные полученные корни являются действительными и отрицательными. Потому при 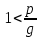 точка точка 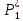 является асимптотически устойчивой. является асимптотически устойчивой. В противном же случае при 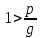 эта точка неустойчива. эта точка неустойчива.Рассмотрим характеристическое уравнение и его решения для точки  . . =0 =0Это уравнение имеет такие корни:   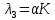 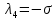 Корень 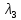 характеристического уравнения действительный и положительный, а корень характеристического уравнения действительный и положительный, а корень 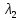 может принимать как отрицательные, действительные, так и положительные, действительные. Следовательно, точка может принимать как отрицательные, действительные, так и положительные, действительные. Следовательно, точка 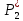 является неустойчивой. является неустойчивой.В результате проведенного исследования мы выявили два положения равновесия, одно из которых асимптотически устойчиво при 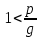 , другое же всегда неустойчиво. , другое же всегда неустойчиво.Точки покоя системы в условиях распространения вирусов Теперь рассмотрим эту же систему дифференциальных уравнений, но с условием распространения вирусов в соответствующей ей модели. В данной системе существует такая точка покоя, при которой система становится стабильно зараженной, то есть часть ее объектов постоянно инфицировано. Точки покоя определим следующим образом: так как в системе распространяются вирусы, то количество инфицированных объектов и удаленных вирусом будем считать не равным нулю, то есть 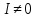 , , 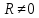 , ,а количество объектов с антивирусным программным обеспечением равно нулю 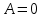 . .Следовательно, система упростится до следующего вида: 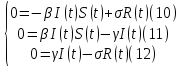 Вычислим значения 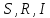 через параметры. через параметры. Для начала найдем 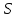 . Для этого уравнение (11) разделим на . Для этого уравнение (11) разделим на 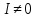 В результате получим 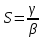 . .Теперь получим 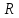 . Из уравнения (12) . Из уравнения (12) 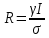 , помня о том, что , помня о том, что 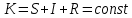 , получаем , получаем 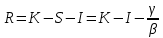 . . Тогда: 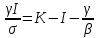 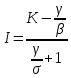  Составим определитель из частных производных функций системы:  Приведем его к диагональному виду:  Подставим найденные выражения:  Собственные значения равны: 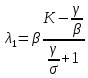 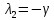 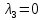 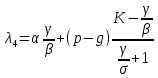 Ясно, для того чтобы все полученные значения были действительными и отрицательными, то есть удовлетворяли теореме об устойчивости точки, необходимо выполнение следующих условий: Первое: 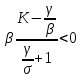 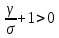 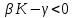 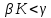  Второе:    В этих случаях система является асимптотически устойчивой, а точка 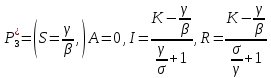 точкой покоя системы. точкой покоя системы.Заключение В результате проделанной работы были достигнуты все цели и задачи, поставленные ранее: рассмотрена эпидемиологическая SAIR-модель распространения вирусов; проведено исследование системы на устойчивость, в результате которого было найдено три положения равновесия 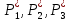 : :точка 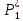 является асимптотически устойчивой только в том случае, когда является асимптотически устойчивой только в том случае, когда 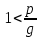 . В противном же случае при . В противном же случае при 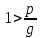 данная точка будет всегда неустойчива; данная точка будет всегда неустойчива;точка 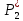 для данной системы всегда неустойчива; для данной системы всегда неустойчива;в точке 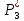 система является асимптотически устойчивой, если выполняются следующие неравенства: система является асимптотически устойчивой, если выполняются следующие неравенства: 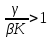 , ,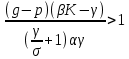 . .Список литературы http://avmaksimov.ucoz.ru/_ld/1/109_-Bratus_A-Novoz.pdf http://e.lib.vlsu.ru/bitstream/123456789/3072/1/00686.pdf Котенко И. В., Воронцов В. В. Аналитические модели распространения сетевых червей // Труды СПИИРАН. Вып. 4. — СПб.: Наука, 2007. http://tkachenko-mephi.narod.ru/pdfs/DIUlec4.pdf http://old.petrsu.ru/Chairs/MMSU/qa_ds.pdf https://www.hse.ru/data/2015/04/08/1095136730/%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D1%8F%202.pdf http://books.ifmo.ru/file/pdf/1790.pdf http://refac.ru/issledovanie-ustojchivosti-po-pervomu-priblizheniyu/ http://portal.tpu.ru/SHARED/p/PEG/page_2/math_analysis-03/Tab2/MA(3)_Lecture-14(fragment).pdf |
