экономические задачи. экономические задачи на печать. Общая схема решения экономических задач
 Скачать 490.69 Kb. Скачать 490.69 Kb.
|
|
ГЛАВА 5. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ Задача 1: .[4] В июле 2016 года планируется взять кредит в банке на три года в размере S млн рублей, где S – целое число. Условия его возврата таковы: - каждый январь долг увеличивается на 30% по сравнению с концом предыдущего года; - с февраля по июль необходимо выплатить одним платежом часть долга; - в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
Найдите набольшее значение S, при котором каждая из выплат будет меньше 5 млн рублей. Ответ: 7 млн рублей Задача 2: .[4] В июле планируется взять кредит в банке на сумму 4,5 млн рублей на срок 9 лет Условия его возврата таковы: - каждый январь долг возрастает на r% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить часть долга; - в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн рублей, а наименьший - не менее 0,6 млн. Ответ: 20% Задача 3. .[4] В июле планируется взять кредит в банке на сумму 9 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы: - каждый январь долг возрастает на 10% по сравнению с концом предыдущего года; - с февраля по июль каждого года необходимо выплатить часть долга; - в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платеж составит 1,5 млн рублей? Ответ: 16,2 млн рублей Задача 4. .[4] В июле планируется взять кредит в банке на сумму 16 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы: - каждый январь долг возрастает на 25% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить часть долга; - в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн рублей? Ответ: 10 лет Задача 5. .[2] 15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы: - 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца; - со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; - 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r. Ответ: 3% Задача 6. .[2] В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы: - каждый январь долг возрастает на 20% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить часть долга; - в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. На сколько лет был взят кредит, если общая сумма выплат после полного погашения кредита составила 7,5 млн рублей? Ответ: 4года Задача 7 .[6] В июле планируется взять кредит в банке на сумму 100 000 рублей. Условия его возврата таковы: - каждый январь долг возрастает на r% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить часть долга. Найдите число r, если известно, что кредит был полностью погашен за два года, причем в первый год было переведено 55 000 рублей, а во второй год – 69 000 рублей. Ответ: 15% Задача 8. [6] В июле планируется взять кредит в банке на сумму 100 000 рублей. Условия его возврата таковы: - каждый январь долг возрастает на r% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить часть долга. Найдите число r, если известно, что кредит был полностью погашен за два года, причем в первый год было переведено 66 000 рублей, а во второй год – 58 000 рублей. Ответ: 16% Задача 9. [6] 15 июля планируется взять кредит на сумму 800 000 рублей. Условия его возврата таковы: - 31-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; - со 2-го по 14-е число каждого месяца необходимо выплатить некоторую часть долга. На какое минимальное количество месяцев можно взять кредит при условии того, чтобы ежемесячные выплаты были не более 200 000 рублей? Ответ: 5 месяцев Задача 10. [6] В июле планируется взять кредит в банке на сумму 8 млн рублей. Условия его возврата таковы: - каждый январь долг возрастает на 25% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить часть долга; - в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года. На какой минимальный срок следует брать кредит, чтобы наибольший годовой платёж по кредиту не превысил 3,6 млн рублей? Ответ: 5 лет ЗАКЛЮЧЕНИЕ Практические задачи задания № 17 сложны для обучающихся отсутствием унифицированных формул в курсе математики школьной программы. Я предположила, что существует множество видов «экономических» задач на проценты и способов их решения, но их можно объединить по типам для облегчения усвоения материала, а также можно самостоятельно вывеси формулы для их решения. С этой целью я занялась исследованием экономических задач. Я изучила теоретические аспекты решения экономических задач и научилась понимать и использовать информацию, представленную в процентах. Познакомилась с видами «экономических» задач из сборников для подготовки к ЕГЭ 2015, 2016, 2017, 2018 гг. и открытого банка задач по математике. Углубила знания по теме проценты. Рассмотрела различные способы решения задач. Выявила структуру экономических задач на проценты. Провела анализ решений. Обобщила и систематизировала способы решения задач. Составила единую схему решения и вывела формулы для решения этих задач. Собрала материал для самостоятельной работы, чем облегчила работу тем, кто будет готовиться к экзаменам по данной методичке. Решив и проанализировав задачи, я пришла к заключению, что большая часть задач сводится к таблице такого вида:
Для понимания задачи всегда можно нарисовать спираль. Таким образом, в ходе своего исследования я заметила: I. что большинство экономических задач можно условно разделить на два типа: А) равный размер выплат Б) сокращение остатка на одну долю от целого. II. имеет общую схему решения: 1.Нарисовать процесс «движения» денег в виде спирали 2. Занести данные в таблицу 3. Составить выражения для всех столбиков таблицы 4. Составить уравнение или неравенство 5. В ходе решения уравнения появится формула, с помощью которой будет найдено неизвестное Формулы экономических задач, которые получены в ходе моего исследования А) равный размер выплат Основная идея для решения этих задач уравнение для последнего остатка: KnS – kn-1x – kn-2x – kn-3x - …. - kx –x = 0 Из этого уравнения выводим формулы для S и X. 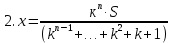 ; ; 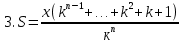 ; ;Б) сокращение остатка на одну долю от целого. Закономерность изменения выплата при её разном значении: 1.S(k-1)+ 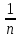 S; S; 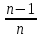 *S(k-1)+ *S(k-1)+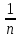 S; S;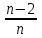 *S(k-1)+ *S(k-1)+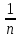 S; … S; … 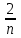 *S(k-1)+ *S(k-1)+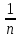 S; S;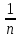 *S(k-1)+ *S(k-1)+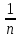 S S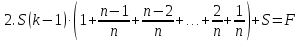 сумма выплат сумма выплатФормула переплаты: 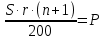 (где P = F – S) (где P = F – S)Так гипотеза, сформулированная нами в начале исследования, подтвердилась. Проведение данного исследования позволило получить практический материал для обучения математике, который также лег в основу моего личностного развития, как выпускника 2017/2018 учебного года и способствовало продуктивному началу подготовке к сдаче экзамена. В дальнейшем планируется использование созданного материала на уроках математики в старших классах школы и расширение спектра экономических задач. Таким образом, понимание процентов, кредитования, крайне полезно и важно, ведь это не только помогает решить задачи профильного уровня ЕГЭ по математике, но и в целом даёт базовое понятие о банковских процессах, что в будущей жизни, несомненно, поможет. В целом работа по данной теме для меня оказалась плодотворной, а также она может представлять интерес для всех, кто сталкивается с математическими расчетами. Кроме того, при исследовании удалось вывести общую схему решения задач, которую можно будет применять в последующих жизненных ситуациях. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ: Интернет-источники: 1.Web –Википедия «Процент»https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%BE%D1%86%D0%B5%D0%BD%D1%82 2.РЕШУ ЕГЭ Образовательный портал для подготовки к экзаменам/ https://math-ege.sdamgia.ru/?redir=1 3.Самообразование. Главная > 2017: ЕГЭ, ОГЭ Предметы > ЕГЭ 2017. Математика. И.В. Ященко. 36 вариантов. Профильный уровень / http://self-edu.ru/ege2017_36.php Литературные источники: 4.И.В.Ященко «ЕГЭ-2018 МАТЕМАТИКА ПРОФИЛЬНЫЙ УРОВЕНЬ» - М., Национальное образование, 2018г. 5. И.В.Ященко «ЕГЭ-2017 МАТЕМАТИКА ПРОФИЛЬНЫЙ УРОВЕНЬ» -М. , Национальное образование , 2017г. 6.А.В. Семенов, И.В.Ященко «КАК ПОЛУЧИТЬ МАКСИМАЛЬНЫЙ БАЛЛ НА ЕГЭ МАТЕМАТИКА »-М., Интеллект -центр , 2015г. 7.А. Г. Малкова «МАТЕМАТИКА АВТОРСКИЙ КУРС ПОДГОТОВКИ К ЕГЭ»_ Ростов – на- Дону, Феникс, 2017г. |
