ответы бух зо. Общая теория статистики Виды абсолютных показателей, их значение
 Скачать 0.81 Mb.
|
|
8. Вариация признаков. Порядок исчисления показателей вариации. Вариация – это колеблемость, изменение величины признака в статистической совокупности, т.е. принятие единицами совокупности разных значений признака. Простейшим показателем вариации признака является вариационный размах. Вариационный размах (амплитуда колебаний) признака рассчитывается как разность между максимальной и минимальной вариантами определённого количества признака в статистической совокупности. Вариационный размах рассчитывают следующим образом:  где Rх – размах вариации признака;  - соответственно конечная (максимальная) и начальная (минимальная) варианты.Основной недостаток вариационного размаха заключается в том, что он не отражает внутренних изменений признака и полностью зависит от отдельных случаев, оказывающихся на обоих полюсах ранжированного ряда. Поэтому вариационный размах используется для поверхностной характеристики вариации признака в статистической совокупности. Среднее квадратической отклонение Среднее квадратической отклонение рассчитывается по простой и взвешенной формах. Для ранжированного ряда рассчитывают невзвешенное (простое) среднее квадратической отклонение по следующей формуле:  где  - среднее квадратической отклонение вариационного признака; х – индивидуальные варианты в ранжированном ряду;  - среднее значение признака в статистической совокупности; n – число вариант в ряду.Взвешенное среднее квадратической отклонение рассчитывают для дискретного ряда:  где fх – частота (веса) в вариационном ряду. Последовательность расчёта взвешенного среднего квадратического отклонения состоит в следующем:
Дисперсия как показатель колеблемости признака не играет какой-либо самостоятельной роли при оценке вариации признака в статистической совокупности. Вместе с тем дисперсия представляет собой особый интерес при рассмотрении и применении дисперсионного метода. 7. Из среднего квадрата отклонений (дисперсии) извлекают квадратный корень, в результате чего получаем среднее квадратическое отклонение. Целесообразно обратить внимание на то, что среднее квадратическое отклонение измеряется в тех же единицах, что и варианты изучаемого признака в статистической совокупности. Оно характеризует среднюю колеблемость вариант в этой совокупности и широко используется в качестве одного из более точных и объективных показателей вариации не только в статистике, но и в технике, биологии, других отраслях знаний. Коэффициент вариации Коэффициент вариации представляет собой относительный показатель, который можно рассчитать по следующей формуле:  где Vх – коэффициент вариации признака х в статистической совокупности;  - среднее квадратическое отклонение признака х; - среднее значение признака в статистической совокупности.Обычно коэффициент вариации выражают в процентах и используют как объективную меру колеблемости вариант в статистической совокупности. В этом случае коэффициент вариации может характеризовать количественную однородность или разнородность изучаемых признаков в составе статистической совокупности. Если же коэффициент вариации выше 10,0%, то статистическая совокупность по заданному признаку считается неоднородной. Коэффициент вариации может быть рассчитан и оценен для любого вида вариационных рядов по формуле:  Коэффициент вариации может быть использован при сравнение колеблемости нескольких признаков как в одной и той же статистической совокупности, так и в различных совокупностях. 9. Сущность выборочного метода. Схемы и способы отбора. Статистическая работа в большинстве случаев так или иначе связана с данными, полученными в результате применения выборочного метода. Многие исследования были бы невыполнимы, если бы не использовались материалы выборочных наблюдений. Так, для оценки качества сельскохозяйственной продукции (зерна, льнотресты, картофеля, кормов, молока, продукции выращивания животных и т.д.) нет никакой необходимости подвергать соответствующему исследованию весь объем валового производства. Для этого из общего объема каждого вида продукции достаточно взять несколько небольших проб, например, при определении жирности молока во время его реализации на перерабатывающих предприятиях из каждой фляги обычно берут для анализа стограммовую навеску. Выборочный метод - метод статистического наблюдения, которое дает характеристику генеральной статистической совокупности на основании обследования некоторой ее части. Выборочное наблюдение достигает своей цели только при условии соблюдения принципов и правил отбора статистических единиц, исключающих субъективность и тенденциозность. Если выборочное наблюдение проведено с соблюдением всех правил научной его организации, то результаты выборки объективно характеризуют генеральную совокупность. Практика применения выборочного метода доказывает, что статистические характеристики, полученные в результате выборочного наблюдения, близки к характеристикам сплошного наблюдения. Как генеральная, так и выборочная совокупности характеризуются своими показателями: средним размером признака, дисперсии, средним квадратическим отклонением, коэффициентом вариации изучаемого признака, долей и другими статистическими характеристиками. Для формального различия между генеральными и выборочными статистическими характеристиками обычно используется специальная символика. Например, если генеральную среднюю обозначают, скажем, через , то аналогичную выборочную среднюю — через  ; генеральную дисперсию -  выборочную дисперсию — соответственно  . В генеральной совокупности доля единиц, обладающих тем или иным признаком, называется генеральной долей, которую можно обозначить через Р. В свою очередь выборочная доля обозначается через d.Выборочный метод имеет ряд преимуществ перед сплошным наблюдением. Во - первых, выборочное наблюдение позволяет существенно экономить труд, средства, время для его проведения. Во-вторых, выборочное наблюдение позволяет достигать большую глубину, детальность и точность регистрации фактов. В самом деле, применение выборочного метола расширяет возможности ввести в программу наблюдения дополнительные вопросы, чем и достигается детальность и, следовательно, большая глубина регистрации. В - третьих; выборочный метод обычно применяют в тех случаях, когда сплошное наблюдение из-за его громоздкости проводить нецелесообразно. Понятно, что под громоздкостью наблюдения понимается слишком большой объем работы, неоправданно растянутые сроки, привлечение значительного числа дополнительных квалифицированных работников и т.д. Учитывая эту позицию, выборочное наблюдение применяют, например, при проведении постоянных бюджетных обследований домашних хозяйств, регистрации цен на рынках, изучении потребительского рынка. В - четвертых, выборочный метод используют в тех случаях, когда сплошное наблюдение проводить невозможно. Это относится, главным образом, к статистическим наблюдениям за качеством продукции, изделий и неизбежно связано с их порчей или разрушением. Перечисленные существенные преимущества выборочного метода "уравновешиваются" значительным недостатком. Дело в том, что распространение результатов выборки на генеральную совокупность неизбежно связано с погрешностью, которую принято называть ошибкой репрезентативности. Эта ошибка формируется вследствие самого факта неполного охвата всех единиц в генеральной совокупности. Отбор статистических единиц из генеральной совокупности может быть произведен no-разному и зависит от многих условий. Выборочный метод включает следующие способы отбора статистических единиц: случайный, механический, типический, серийный, многоступенчатый и др. Случайный отбор - наиболее простой способ, который представляет такую организацию выборочного наблюдения, при которой отбор статистических единиц из сплошной (генеральной) совокупности производится случайно, наугад или по жребию. При этом обеспечивается равная вероятность каждому элементу генеральной совокупности попасть в выборку. Однако этот способ отбора не может обеспечить минимальную ошибку репрезентативности. Тем не менее, при соблюдении необходимых условий проведения выборочного наблюдения случайный отбор позволяет дать объективную оценку генеральной совокупности. Случайный отбор может быть повторным и бесповторным. При повторном отборе обследованная выборочная статистическая единица подлежит возврату обратно в генеральную совокупность. Случайный повторный отбор применяют в тех случаях, когда число единиц в генеральной совокупности относительно невелико. Целесообразно отметить, что случайный повторный отбор, имеющий распространение в технике, в социально-экономических исследованиях применяется редко. При случайном бесповторном отборе статистические единицы наблюдения в генеральную совокупность не возвращаются. Бесповторный отбор применяется в тех случаях, когда генеральная совокупность по числу единиц достаточно велика; при этом не требуется возврат отобранных единиц. Эта разновидность случайного отбора по сравнению со случайной повторной выборкой дает более точные результат. Механический отбор, в отличие от случайной выборки, заключается в отборе статистических единиц из генеральной совокупности в каком-либо механическом порядке. Механическая выборка предполагает определенную последовательность ее проведения: во-первых, все статистические единицы генеральной совокупности размещают по заданному признаку в определенном порядке, например, по алфавиту или по ранжиру; во-вторых, из полученного ряда (генеральной совокупности) отбирают, например, каждую пятую, десятую, двадцатую, сотую и т.д. статистическую единицу для проведения выборочного наблюдения. Промежуток, через который попадают единицы в выборку, зависит от принятой пропорции отбора. Эта пропорция устанавливается отношением численности генеральной совокупности на объем выборки. Так, если предполагается отобрать каждую десятую единицу из общего числа 1000 единиц, то в выборку попадает 100 единиц. Следовательно, из генеральной совокупности может быть взята, например, каждая первая, одиннадцатая, двадцать первая, тридцать первая и т.д. единица. Возможен и другой вариант отбора, т.е. берут, например, каждую пятую, пятнадцатую, двадцать пятую, тридцать пятую, и т.д. единицу. Опыт показывает, что при взятии за начало отсчета числа, лежащего в середине интервала, ошибка выборки будет минимальной. Механический отбор позволяет свести ошибки репрезентативности до минимума, что является основным его преимуществом. Однако этот способ более трудоемок, менее экономичен и более сложен по сравнению, например, со случайной выборкой. Кроме того, механический отбор ограничен в применении, так как не по всякой генеральной совокупности можно разместить статистические единицы в определенной последовательности. Типический отбор. При этом способе отбора статистических единиц последовательность выполнения работ заключается в следующем: во-первых, все единицы генеральной совокупности разбиваются на однородные в качественном отношении группы по типическому признаку; во-вторых, из каждой типической группы отбирается намеченное количество статистических единиц по принципу случайной или механической выборки. Целесообразно отметить, что отбор единиц внутри каждой типической группы может быть как пропорциональным, так и непропорциональным. При пропорциональном отборе число единиц зависят от их общего количества в каждой типической группе, при непропорциональном - число отобранных единиц не зависит от представительности типических групп. Например, для проведения выборочного наблюдения необходимо отобрать перерабатывающие предприятия АПК различного профиля: по переработке зерна, картофеля, льнотресты, молока и т.д. В этом случае все перерабатывающие предприятия (генеральную совокупность) необходимо сгруппировать по их типичному производственному профилю, например, зерноперерабатывающие, картофелеперерабатывающие и т.д. Далее, из каждой сформированной группы для проведения выборочного наблюдения отбираем, скажем, по 20 предприятий независимо от их общего числа в группе. Но так как общее число перерабатывающих предприятий в каждой группе может существенно различаться, то в этом случае имеет место непропорциональный отбор. Если же отбор предприятий из каждой типической группы будет проведен согласно структуре всех предприятий, т.е. по их удельному весу в общей численности, то по каждой типической группе в выборку может попасть не строго по 20, а различное число предприятий. Это означает, что имеет место пропорциональный отбор. Типический отбор отличается относительной сложностью проведения, повышенной трудоемкостью и невысокой экономичностью, Кроме того, типический отбор, подобно механическому, ограничен в применении. Вместе с тем использование типического отбора позволяет обеспечить минимальную ошибку репрезентативности. Серийный отбор. Сущность этого способа значительно отличается от других способов отбора статистических единиц. Серийный отбор проводится в следующем порядке: во-первых, генеральная совокупность разбивается на однотипные в качественном отношении группы, называемые сериями (гнездами); во-вторых, из генеральной совокупности отбирают отдельные серии (гнезда), которые по числу статистических единиц могут быть как равновеликими, так и неравновеликими; в-третьих, в отобранных сериях проводится сплошное наблюдение всех статистических единиц. Серийная выборка может проводиться в порядке как повторного, так и бесповторного отбора. Отличаясь относительной простотой и экономичностью выполнения, она может обеспечить сравнительно невысокую погрешность результатов выборочного наблюдения. Особенно широко используется серийный отбор при проведении контроля оплаты за проезд в автобусах, троллейбусах, трамваях, пригородных поездах, где все пассажиры каждого контролируемого транспортного средства представляют собой серию статистических единиц в составе генеральной совокупности (всего пассажиропотока). 10. Ошибки выборочного наблюдения, их сущность и методика расчета. Одним из центральных вопросов по выборочному методу считается теоретический расчет основных статистических характеристик и прежде всего среднего значения признака в генеральной статистической совокупности. Это означает, что теоретически рассчитанная средняя выборочная величина и другие выборочные характеристики должны лишь минимально отличаться от соответствующих им генеральных статистических характеристик, т.е. выборка всегда должна давать достоверные, надежные, репрезентативные результаты. Значение средней величины в генеральной совокупности может быть теоретически рассчитано по даннным выборочной статистической совокупности следующим образом:  где - среднее значение признака в генеральной совокупности; - среднее значение признака в выборочной совокупности; Δх - предельная ошибка выборки (предельная погрешность).Формула 7.1 показывает, что среднее генеральное значение теоретически может отклоняться от среднего выборочного значения в большую или меньшую сторону на некоторую величину предельной погрешности. В cвoю очередь, предельную ошибку выборки (Δх) теоретически можно рассчитать по формуле:  гдe t - доверительной коэффициент, зависящими от уровня вероятности Р; Мх — средняя ошибка выборки. Доверительный коэффициент (t) означает, что по расчетному признаку генеральная совокупность "накрывается" доверительной областью. Он должен быть достаточно большим, т.е. отвечать принципу практической достоверности, надежности. Доверительный коэффициент находится по специальной таблице, представляющей собой интегральную математическую функции нормального распределения. Величина средней ошибки выборки зависит от вариации изучаемого признака в генеральной совокупности, объема (доли) выборки и способа отбора. В связи с этим существует несколько приемов расчета средней ошибки выборки. Средняя ошибка выборки при повторном отборе рассчитывается следующим образом:  где МX — средняя ошибка выборки; - среднее квадратическое отклонение признака в выборочной совокупности; n - число вариант выборочной совокупности (численность выборки).Средняя ошибка выборки для бесповторного отбора может быть найдена по следующей формуле: 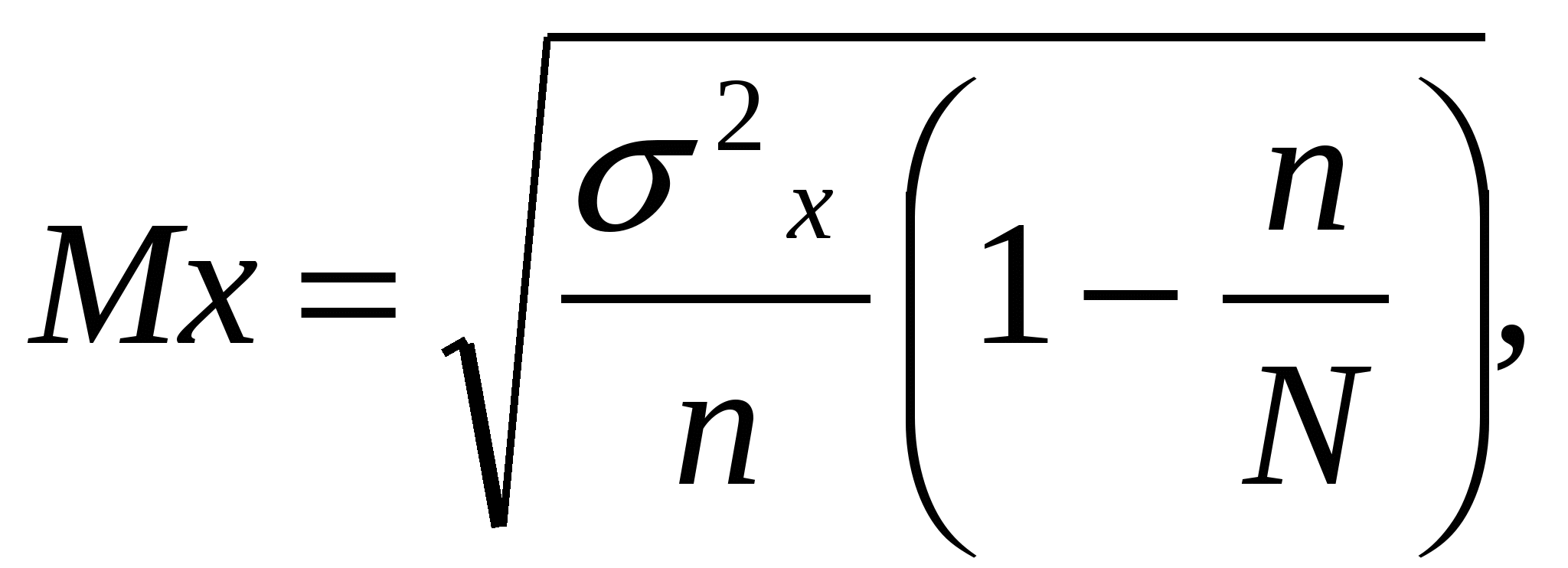 где - дисперсии признака в выборочной совокупности; N - число единиц в генеральной совокупности (численность генеральной совокупности).Если сравнить среднюю ошибку выборки, рассчитанную по формулам 7.3 и 7.4, то можно заметить, что с повышением численности выборки и ее приближения к генеральной численности величина средней ошибки неизбежно сокращается. В некоторых случаях варианты признака могут быть представлены в форме удельного веса (доли) например, доля сортовых посевов в общей посевной площади культур, доля чистопородного поголовья в общей посевной площади культур, доля чистопородного поголовья в общей численности голов и дp. Среднюю ошибку выборочной доли при повторном отборе можно рассчитать следующим образом:  , гдe dх - выборочная доля признака; n - численность выборки. Среднюю ошибку выборочной доли при бесповторном отборе можно найти по формуле:  где N - численность генеральной совокупности. |
).
и суммируют - 
.
полученный результат представляет собой средний квадрат отклонений (дисперсию).