ответы бух зо. Общая теория статистики Виды абсолютных показателей, их значение
 Скачать 0.81 Mb.
|
|
4. Индивидуальные и общие агрегатные индексы. Принципы их построения. Индексы различаются по ряду признаков. В зависимости от объектов исследования различают индексы объемных (количественных) и индексы качественных показателей. К объемным относятся индексы, с помощью которых сравниваются количества, общие размеры совокупности того или иного явления. Это, например, индексы физического объема промышленной, сельскохозяйственной продукции, национального дохода и др. Во всех этих индексах количество обычно принято оценивать в неизменных (сопоставимых) ценах. В свою очередь к качественным относятся индексы цен, себестоимости производства продукции, производительности труда, урожайности и другие индексы. Все они исчисляются при сопоставимых фиксированных объемных показателях. По степени охвата элементов совокупности различают индивидуальные, групповые и общие индексы. Индивидуальные индексы дают сравнительную характеристику отдельных элементов той или иной совокупности. Примером индивидуальных индексов может быть изменение объема производства какого-нибудь одного вида продукции, цен на один вид товара, урожайности одной культуры и т.д. Индивидуальные индексы количества какого-либо вида продукции рассчитываются по формуле:  где iq – индивидуальный индекс физического объема (количества) товара; q1, q0, физический объем (количество) товара соответственно в отчетном и базисном периодах. Индивидуальные индексы цены какого-либо вида продукции рассчитываются по формуле:  где iр – индивидуальный индекс цены товара; р1, р0, цена товара соответственно в отчетном и базисном периодах. Общие индексы характеризуют изменение всей совокупности в целом. Общий индекс физического объема определяют по следующей формуле:  Общий индекс цен определяют по следующей формуле:  Общий индекс стоимости продукции определяют по следующей формуле:  5. Сущность средних взвешенных арифметических и гармонических индексов. Основной формой общих индексов является агрегатный индекс, который представляет собой отношение агрегатов, т.е. соединений различных (однородных и неоднородных) элементов сложного показателя, приведенного к сопоставимому виду. Числитель этого индекса расчитывают как сумму произведений индексируемой величины отчетного периода на веса (соизмерители). Знаменатель агрегатного индекса находят как сумму произведений индексируемой величины базисного периода на те же веса (соизмерители). Выбор формы агрегатного индекса непосредственно зависит от наличия исходной информации. Если эта информация представляет собой полное сочетание абсолютных данных о количественных и качественных признаках за сравниваемые периоды или по территориальным объектам, то можно воспользоваться стандартными формулами расчета агрегатных индексов. Так, для расчета общего индекса физического объема товаров стандартную формулу обычно записывают так:  В свою очередь общий индекс цен на товары выглядит следующим образом:  Однако в ряде случаев для расчета общих индексов исходная информация может носить видоизмененный характер. Например, вместо количества товаров, цен в базисном или отчетном периодах имеются индивидуальные индексы, либо коэффициенты роста (прироста) физического объема, цен. В такой ситуации стандартные формулы общих индексов могут быть преобразованы в средние арифметические или средние гармонические индексы. Проведем теоретические преобразования стандартных агрегатных индексов в средние на примере общих индексов прежде всего физического объема товаров. Из формулы индивидуального индекса физического объема следует, что  а  . Подставив в числитель агрегатного индекса физического объема (формула 12.6) вместо отчетного количества q1 равнозначные ему произведения iqq0, получим средний арифметический индекс физического объема: Допустим, организация по переработке овощей и фруктов продала консервированную продукцию за два периода. Фактические результаты реализации и вспомогательные расчеты приведены в табл. Т а б л и ц а . Динамика реализации консервированной продукции
Необходимо найти общий индекс физического объема, т.е. определить, как изменилась стоимость проданной продукции за счет ее физического объема. Данные, полученные в табл. , подставим в формулу, получим:  Полученный общий индекс показывает, что в перерабатывающей организации стоимость проданной консервированной продукции в отчетном периоде по сравнению с базисным увеличилась в 1,054 раза (на 5,4 %) за счет динамики (изменения) физического объема (количества) продукции. Если в стандартную формулу вместо q0 подставить 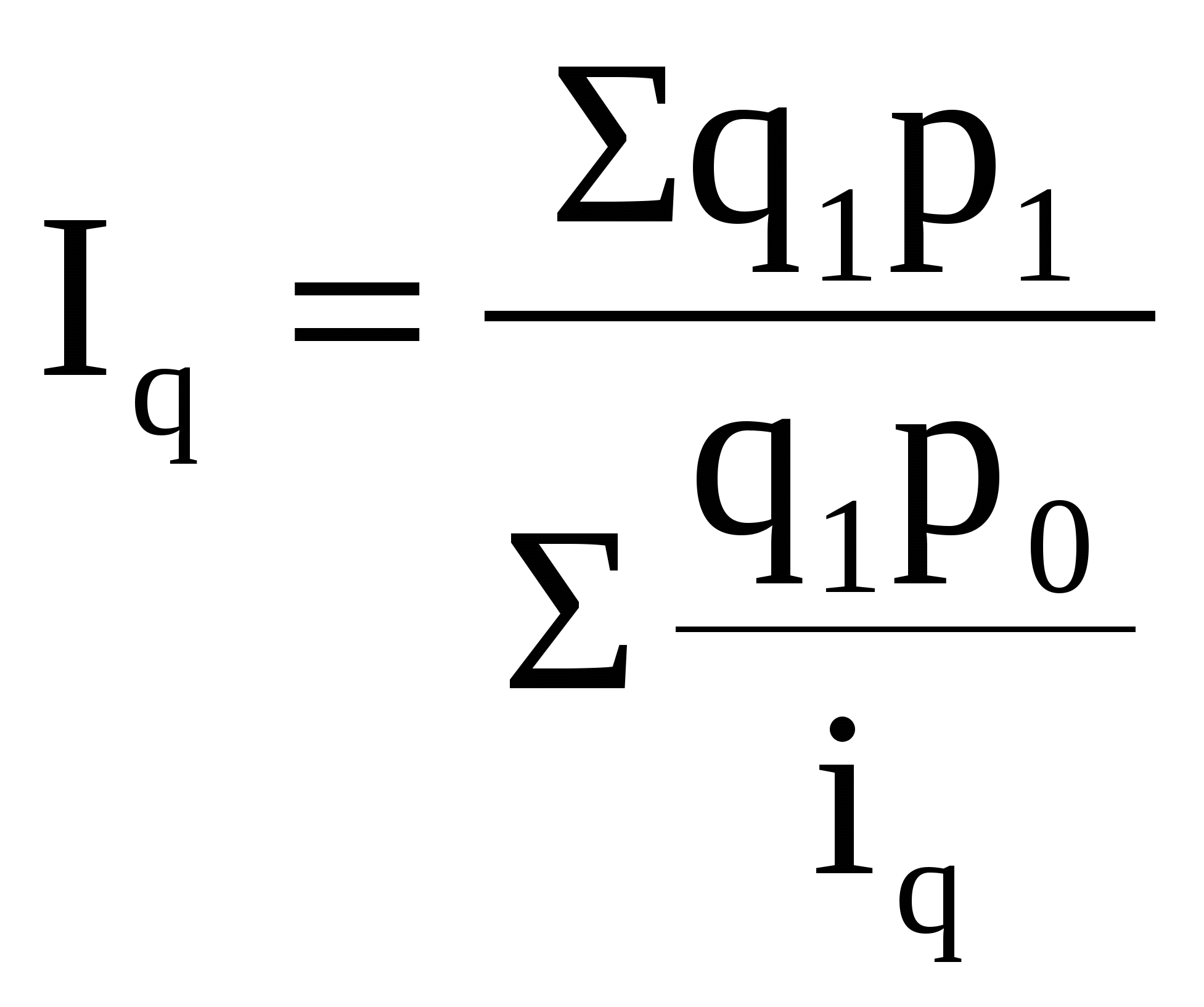 то получим средний гармонический индекс физического объема: . Для примера воспользуемся данными о реализации продукции организации по переработке овощей и фруктов (табл.), где приведены не только фактические результаты продажи, но и вспомогательные расчеты. Т а б л и ц а . Динамика товарной продукции перерабатывающей организации
Необходимо найти общий индекс физического объема и оценить, как изменилась стоимость товарной продукции за счет ее физического объема. Теперь подставим данные табл. в формулу ; получим:  Полученный средний гармонический индекс физического объема (1,054) – это не простое совпадение со средним арифметическим индексом, а свидетельство того, что к одному и тому же результату можно прийти различными приемами. Для преобразования стандартной формулы общего индекса цен в средней арифметический индекс необходимо иметь в виду, что индивидуальный индекс цен  Заменив в числителе стандартного агрегатного индекса цены отчетного периода р1 на ip p0 , получим средний арифметический индекс цен: Если же в знаменателе стандартной формулы агрегатного индекса базисные цены р0 заменить на равнозначные им отношения 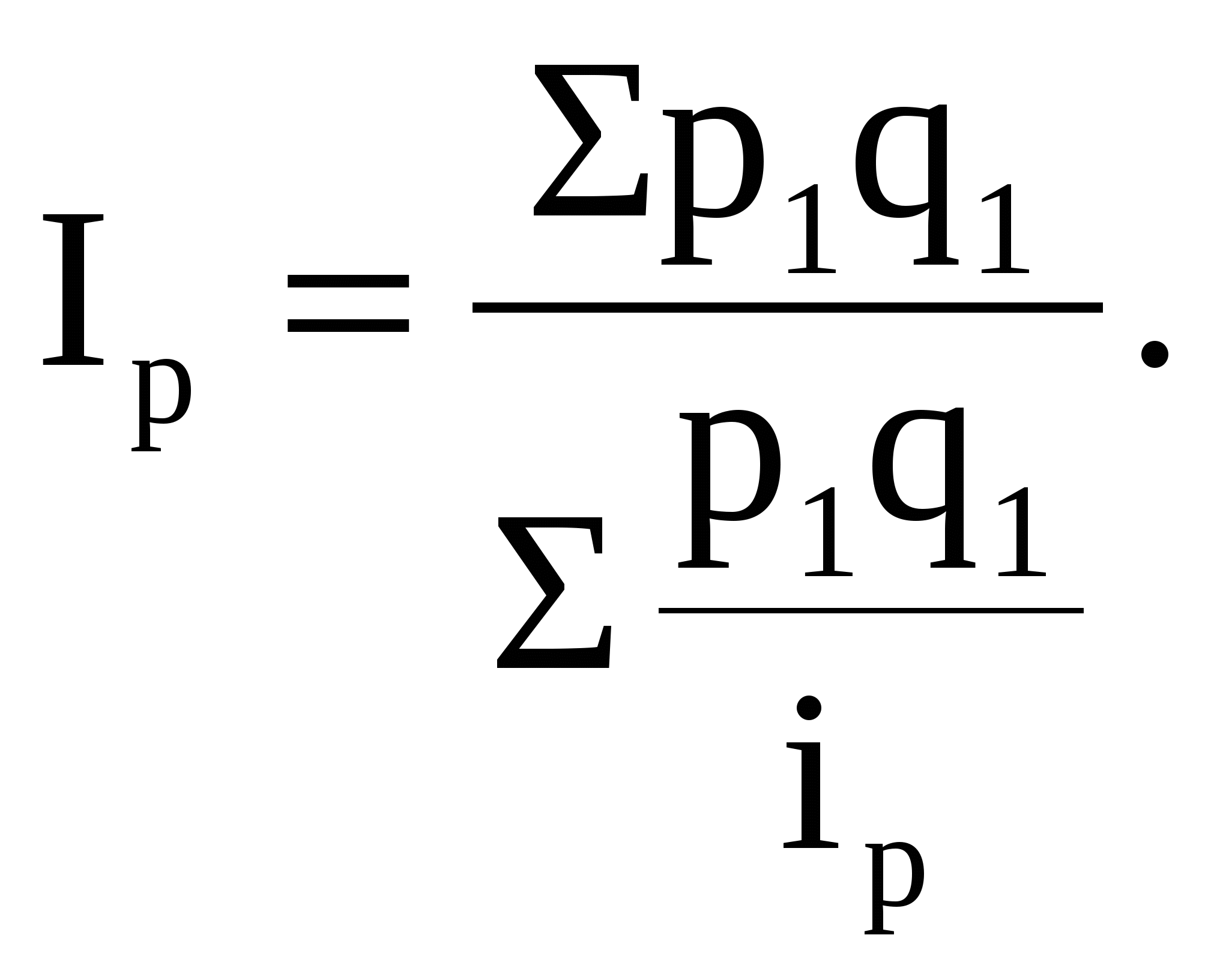 то получим средний гармонический индекс цен: Для закрепления теоретических положений по применению среднего гармонического индекса цен воспользуемся примером. Допустим, сельскохозяйственная организация реализовала продукцию животноводства в первом и втором кварталах календарного года. Исходные данные и вспомогательные расчеты приведены в табл. Т а б л и ц а . Динамика реализации животноводческой продукции сельхозорганизации
Необходимо определить, как изменилась стоимость продукции во втором квартале по сравнению с первым за счет реализованных цен. Данные табл. позволяют рассчитать средний гармонический индекс цен (по формуле):  Следовательно, стоимость проданной продукции животноводства во втором квартале по сравнению с первым кварталом за счет цен реализации возросла в 1,172 раза, или на 17,2 %. 6. Сущность средней как статистического показателя. Средняя арифметическая, область ее применения. Средняя величина – это обобщенная количественная характеристика признака в статистической совокупности. Она выражает типичное значение признака для всех единиц совокупности под влиянием всего комплекса факторов. В средней величине погашаются индивидуальные различия единиц совокупности и вариантах усредняемого признака. Средняя величина является важнейшей категорией статистической науки и важнейшей формой обобщающих показателей. Многие явления и процессы становятся ясными, определенными, лишь будучи обобщенными в форме средних величин. Таковы, например, средняя урожайность, средняя продуктивность животных, средняя производительность труда, средняя себестоимость единицы продукции, средняя заработная плата, средний душевой доход и т.д. Основным условием правильного применения средних величин является качественная однородность статистической совокупности. Среднее, вычисленные для качественно неоднородной совокупности, теряют свое научное значение. Такие средние являются фиктивными, причем не только не имеющими представление действительности, но искажающими ее и вводящими в заблуждение, так как они стирают существенные различия между явлениями. Средняя арифметическая величина. Средняя арифметическая простая величина:  , где n – число единиц в статистической совокупности. Средняя арифметическая величина взвешенная величина определяется по формуле:  . где f – локальные частоты (частости). Расчет средней арифметической простой можно показать на примере ранжированного ряда, составленного по площади посева льна-долгунца в 20 сельскохозяйственных предприятиях района (табл. 6.1.). Т а б л и ц а. Расчет средней арифметической простой в ранжированном ряду распределения
Подставив данные табл. в формулу, получаем среднее арифметическое простое значение посевной площади льна-долгунца, приходящиеся на 1 хозяйство:  Поскольку в дискретном ряду распределения каждая варианта представлена определенной локальной частотой (частостью), то среднее значение для каждого такого ряда может быть рассчитано по формуле средней арифметической взвешенной, т.е. , где х – варианты (значение признака); f – локальные частоты (частости). Определение средней арифметической взвешенной величины можно показать на примере расчёта средней урожайности льносоломки в 20 сельскохозяйственных предприятиях района, поскольку в этих предприятиях разная посевная площадь (f) (табл.). Подставив в формулу данные табл., можно рассчитать среднюю арифметическую взвешенную величину для дискретного ряда распределения:  Таким образом, средняя урожайность, взвешенная по посевной площади льна-долгунца, в сельскохозяйственных предприятиях района, составила 50 ц/га льносоломки. Т а б л и ц а 6.2. Расчет средней арифметической взвешенной в дискретном | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
