Лабораторная по ИОиМО №1. Общая задача линейного программирования. Оптимальные бизнеспланы, план по продукции, технология оптимизации
 Скачать 93.12 Kb. Скачать 93.12 Kb.
|
|
Выполнила студентка академической группы РФ16ДР62ПЭ Бойко А. Ю. Отчёт по лабораторной работе №1 Тема: Общая задача линейного программирования. Оптимальные бизнес-планы, план по продукции, технология оптимизации. Цель: познакомиться с задачами линейного программирования; научиться строить экономико-математическую модель задачи, научиться стоить табличную модель и находить оптимальное решение при помощи надстройки «Solver», научиться составлять наилучший (оптимальный) план производства продукции с учетом ограниченного обеспечения материальными ресурсами, проводить анализ полученных результатов. Задача № 1 Рассмотрим преобразование задачи коммерческой деятельности к общей ЗЛП и построение экономико-математической модели на примере. Коммерческому отделу поручили проанализировать совместную деятельность подразделений фабрики по изготовлению и продаже двух видов краски для внутренних (В) и наружных (Н) работ, которая поступает в продажу по цене 3 тыс. руб. и 2 тыс. руб. за 1 т. Для производства красок используют два вида сырья А и В, максимально возможные суточные запасы которых составляют 3 т и 4 т. Расходы сырья на производство 1 т красок приведены в табл.1. Таблица 1
Какое количество краски каждого вида необходимо производить, чтобы доход от ее реализации был максимальным? Для решения поставленной задачи была построена табличная модель (рис. 1).  Рис. 1. Табличная модель с результатами решения В данной задаче целевой функцией является максимальный доход. Было представлено 2 вида сырья, А и В, при запасе их соответственно 3 и 4 тонны. При помощи поиска решений был получен оптимальный объём производства краски для наружных работ 3,3 тонны, а краски для внутренних работ 1,3 тонны. Исходя из полученных результатов, примерный доход составил 10,7 тыс. руб. Задача № 2 Предприятие выпускает телевизоры, стерео- и акустические системы, используя общий склад комплектующих. Каждому типу изделий соответствует своя норма прибыли. Запас комплектующих на складе ограничен. Задача сводится к определению количества каждого вида изделий для получения наибольшей прибыли, т. е. оптимальное соотношение объемов выпуска разных типов изделий в плане. Для решения поставленной задачи была построена табличная модель (рис. 2). 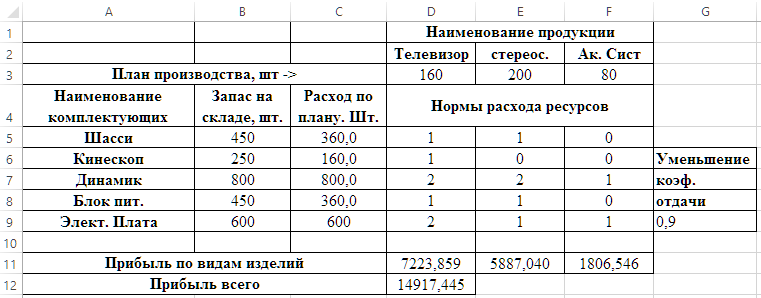 Рис. 2. Табличная модель с результатами решения В данной задаче целевой функцией является максимальный доход. Предприятие выпускает телевизоры, стерео- и акустические системы соответственно 160, 200 и 80 штук. При помощи поиска решений была получена прибыль по каждому виду продукции, она составила 7223,859 рублей по телевизорам, 5887,04 рублей по стереосистемам и по акустическим системам 1806,546 рублей. Оптимальная прибыль по всем видам продукции составила 14917,445 рублей. Индивидуальное задание Кондитерская фабрика в Покрове освоила выпуск новых видов шоколада «Лунная начинка» и «Малиновый дождик», спрос на которые составляет соответственно не более 12 и 7 т в месяц. По причине занятости трех цехов выпуском традиционных видов шоколада каждый цех может выделить только ограниченный ресурс времени в месяц. В силу специфики технологического оборудования затраты времени на производство шоколада разные, данные представлены в таблице 2. Таблица 2
Необходимо определить оптимальный объем выпуска шоколада, обеспечивающий максимальную выручку от продажи. Для решения поставленной задачи была построена табличная модель (рис. 3).  Рис. 2. Табличная модель с результатами решения В данной задаче целевой функцией является максимальная прибыль. Предприятие производит шоколад, под названием «Лунная начинка» и «Малиновый дождик», в трех цехах. При помощи поиска решений был найден оптимальный объем изготовленной продукции, он составил 10,8 тонн шоколада «Лунная начинка» и 4,8 тонн шоколада «Малиновый дождик». А так же найдена оптимальна прибыль по всем видам продукции, которая составила 1152 рублей. Вывод: В ходе выполнения лабораторной работы ознакомились с задачами линейного программирования. Также научились строить экономико-математическую модель задачи, научились строить табличную модель и находить оптимальное решение при помощи надстройки «Solver». Также научились составлять оптимальный план производства продукции с учётом ограничений ресурсов. | ||||||||||||||||||||||||||||||||||||||||
