Материаловедение. Общетехнический курс материаловедение

• Название: Общетехнический курс материаловедение
• Анкор: Материаловедение
• Дата: 23.03.2022
• Размер: 1.24 Mb.
• Имя файла: Материаловедение.doc
• Тип: Тематический план; #411633
• страница: 3 из 13

Механические свойства металлов и сплавов.

Свойства материалов при расчетах на прочность, жесткость и устойчивость определяются механическими характеристиками. Величины механических характеристик могут быть получены в лабораторных условиях доведением образцов до разрушения или чрезмерной деформации. Испытания могут проводить на деформации растяжения, сжатия, кручения, изгиба при действии статической или переменной нагрузок.

Наибольшее распространение имеют испытания на растяжение статической нагрузкой, так как они наиболее просты и дают достаточную информацию о поведении материала при других видах деформации.

Как известно, различные металлы и сплавы имеют разные механичес­кие и технологические свойства, которые предопределяют качество дета­лей машин, а также обрабатываемость металла. Эти свойства металла выявляют соответствующими испытаниями на растяжение, сжатие, изгиб, твердость и др.

И 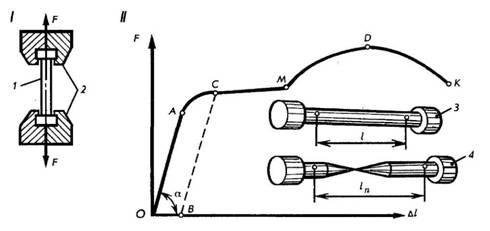спытание на растяжение. Чтобы определить прочность металла, работающего на растяжение, изготовляют образец 1 и устанавливают его в зажимы (или захваты) 2 разрывной машины. Для этих целей чаще всего ис­пользуют машины с гидравлической системой передачи усилия или с вин­товой системой.

Растягивающая сила F (рис. 1) создает напряжение в испытываемом об­разце и вызывает его удлинение. Когда напряжение превысит прочность об­разца, он разорвется.

Рис. 1

Результаты испытания обычно изображают в виде диаграммы. По оси абсцисс откладывают нагрузку F, по оси ординат — абсолютное удлине­ние. Из диаграммы видно, что вначале образец удлиняется пропорционально нагрузке. Прямолинейный участок OA соответствует обратимым, упругим деформациям. При разгрузке образец принимает исходные размеры (этот процесс описывается все тем же прямолинейным участком кривой). Ис­кривленный участок АС соответствует необратимым, пластическим дефор­мациям. При разгрузке (штриховая прямая СВ) образец не возвращается к начальным размерам и сохраняет некоторую остаточную деформацию.

От точки С образец удлиняется без увеличения нагрузки. Горизонталь­ный участок СМ диаграммы называется площадкой текучести. Напряжение, при котором происходит рост деформаций без увеличения нагрузки, называется пределом текучести.

Как показывают исследования, текучесть сопровождается значительными взаимными сдвигами кристаллов, в результате чего на поверхности образца по­являются линии, наклонные к оси образца под углом 45°. Претерпев состояние текучести, материал снова обретает способность сопротивляться растяжению (упрочняется), и диаграмма за точкой М поднимается вверх, хотя бо­лее полого, чем раньше. В точке D напряжение образца достигает своей наи­большей величины, и на образце появляется резкое местное сужение, так назы­ваемая шейка. Площадь сечения шейки быстро уменьшается и, как следст­вие, происходит разрыв образца. На диаграмме положению точки К. Предел прочности образца определяют по формуле о_пч = F_D / S, где: S_пч — предел прочности;

F_D — нагрузка, при которой через определенный промежуток време­ни наступает разрушение растянутого образца, Н (кгс); S — площадь поперечного сечения образца в исходном положении, м² (мм²).

Обычно при испытании различных металлов и сплавов на растяжение определяют относительное удлинение δ — отношение прироста длины об­разца до разрыва к начальной длине образца. Его определяют по формуле δ = L-L₀ /L_0*100%,

где: δ — относительное удлинение;

L =L_{1 _}—_{__}L₀ абсолютное удлинение; L₀ — начальная длина образца; L₁ — длина образца после испытания. Экспериментально было установлено, что напряжение в материале при упругой деформации возрастает пропорционально относительному удлине­нию образца. Эта зависимость получила название закона Гука.

Для одностороннего (продольного) растяжения закон Гука имеет вид Е =А/s

где: Е = F/s — нормальное напряжение; F — растягивающая сила; s — площадь поперечного сечения;

Е — постоянная величина, зависящая от материала стержня.

Примечание. В системе СИ единицей измерения напряжений служит Пас­каль — напряжение, вызванное силой 1 ньютон (Н), равномерно распределенной по нормальной к ней поверхности площадью 1 м².

1 Па = 0,102 • 10^-4 кгс/см²;

1 Па = 0,102 • 10^-6 кгс/мм²;

1 кгс/см² = 9,81 • 10⁴ Па;

1 кгс/мм² = 9,81 • 10⁶ Па.

В связи с тем, что единица напряжения паскаль очень мала, приходится пользо­ваться более крупной единицей — мегапаскаль 1 МП а = 10⁶ Па.

Госстандарт допускает к применению единицу ньютон на квадрат­ный миллиметр (Н/мм²). Числовые значения напряжений, выраженные в Н/мм² и в МПа, совпадают. Единица Н/мм² удобна и потому, что размеры на чер­тежах проставляют в миллиметрах.

Коэффициент пропорциональности Е называется модулем упругости при растяжении или модулем Юнга. Каков физический смысл моду­ля упругости? Обратимся к диаграмме растяжения образца (см. рис. 1). Модуль упругости на ней пропорционален тангенсу угла наклона а к оси аб­сцисс. Значит, чем круче прямая OA, тем жестче материал, и тем большее сопротивление оказывает он упругой деформации.

Для характеристики металла важно знать не только относительное удли­нение , но и относительное сужение площади поперечного сечения, кото­рое также позволяет характеризовать пластичность материала.

Естественно, что при растяжении образца площадь поперечного сечения уменьшается. В месте разрыва она будет наименьшей. Относительное суже­ние определяют по формуле ψ = (S₀ — S₁) / S₀ • 100%,

где: ψ — относительное сужение;

S₀ — площадь поперечного сечения образца до испытания; S₁ — площадь сечения образца в месте разрыва (в шейке).

Чем больше относительное удлинение и относительное сужение попереч­ного сечения образца, тем более пластичен материал.

Кроме трех рассмотренных характеристик механических свойств метал­лов: предела прочности (o_пч), относительного удлинения (е) и относитель­ного сужения (?), можно определить, пользуясь записанной на машине ди­аграммой, предел упругости (о_y) и предел текучести (о_m),

Испытание на сжатие. Для испытания металлов на сжатие (рис. 2) чаще всего применяют прессы, в которых сжимающая сила образуется путем увеличения гидравлического давления. При сжатии образца из плас­тичного материала, например малоуглеродистой стали (рис. 2. I), его по­перечные размеры увеличиваются, в то время как длина значительно уменьшается. Нарушение целостности образца при этом не происходит (рис. 3). Из диаграммы сжатия (рис. 2, II) видно, что в начальной стадии нагружения деформация возрастает пропорционально нагрузке, затем де­формация резко возрастает при незначительном увеличении на­грузки, далее рост деформации постепенно замедляется вследст­вие увеличения сечения образца.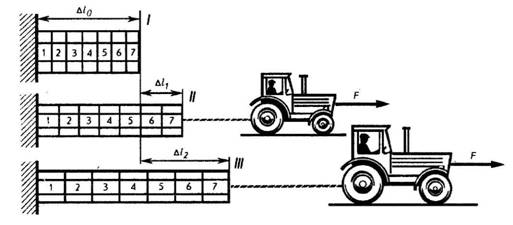



Рис. 2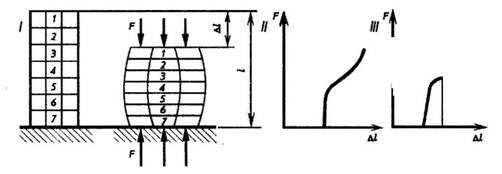



Рис. 3

Образцы из хрупких материалов при сжатии разрушаются (рис. 4, III). Например, стержень из чугуна при достижении разруша­ющей нагрузки распадается на части, которые сдвигаются относительно друг друга по косым площадкам (рис. 3, III).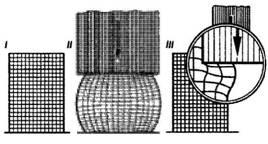



Рис. 4

Для сжатия полностью применим закон Гука, согласно которому мате­риалы противодействуют сжатию пропорционально приложенной силе до предела упругости. Модуль упругости при сжатии для большинства мате­риалов равен модулю упругости при растяжении. Исключение составля­ют только некоторые хрупкие материалы — бетон, кирпич и т. д. Анало­гия в характере напряжения сжатия с напряжением растяжения позволяет описывать эти процессы одними и теми же математическими уравнени­ями.

Испытание на изгиб. При испытании на изгиб образец (брус) укла­дывают концами на две опоры и в середине нагружают (рис. 5). О сопро­тивлении материала изгибу судят по величине прогиба образца.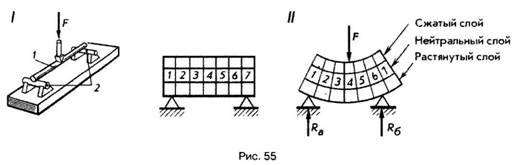



Рис. 5

Представим теперь себе в брусе воображаемые продольные волокна. При деформации изгиба волокна одной зоны сжимаются, другой — растягива­ются (рис. 5, II).

Между зонами сжатия и растяжения расположен нейтральный слой, во­локна которого не подвергаются деформации, то есть их длина не изменяет­ся. Из рис. 5 видно, что, чем больше волокна расположены от нейтрально­го слоя, тем большую деформацию они испытывают. Таким образом, мож­но сделать вывод, что при изгибе в поперечных сечениях бруса под действи­ем внутренних сил возникают нормальные напряжения сжатия и растяже­ния, величина которых зависит от положения рассматриваемых точек в се­чении.

Испытание на срез. При испытании на срез (рис. 6) металличес­кий образец 3, имеющий цилиндрическую форму, вставляют в отверстие приспособления, представляющего собой вилку 1 и диск 2. Машина вы­тягивает диск из вилки, вследствие чего происходит перемещение сред­ней части образца относительно крайних его частей. Рабочая площадь S (площадь среза) равна удвоенной площади поперечного сечения образца, так как срез происходит одно­временно по двум плоско­стям.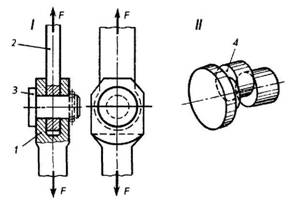



Рис. 6

При срезе все точки дефор­мируемых сечений, ограни­ченных плоскостями действу­ющих сил, смещаются на рав­ные расстояния, то есть мате­риал в этих точках испытыва­ет одинаковую деформацию. Это означает, что во всех точ­ках сечения будут одинако­вые действующие напряже­ния.

Величину напряжения оп­ределяют делением равнодействующей F внутренних (поперечных) сил на площадь поперечного сечения стержня S. Так как вектор напряжения рас­положен в плоскости сечения, в ней возникает касательное напряжение, определяемое по формуле r_ср = F/2S, где: r_ср — величина напряжения среза;

F — равнодействующая сила;

S — площадь поперечного сечения образца. Срез — это разрушение в результате сдвига одной части материала отно­сительно другой, возникающее под действием касательных напряжений. Для деформации сдвига справедлив закон Гука: в зоне упругости напряже­ния прямо пропорциональны относительным деформациям. Коэффициен­том пропорциональности служит величина модуля упругости при сдвиге G. Относительный сдвиг (угол сдвига) обозначается у. Таким образом, закон Гука для деформации сдвига имеет вид t = Gg, где: r = F/S — касательное напряжение; F — касательная сила; S — площадь сдвигающихся слоев; y — угол сдвига;

G — модуль сдвига, зависящий от материала тела.

И 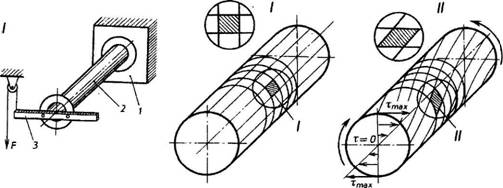спытание на кручение. При испытании образцов на кручение один конец трубы 2 закрепляют неподвижно 1, другой вращают с помо­щью рычага 3 (рис. 7). Кручение характеризуется взаимным поворотом поперечных сечений стержня, вала, трубы под влиянием моментов (пар сил), действующих в этих сечениях. Если на поверхности стержня до приложения сил кручения нанести прямолинейные образующие (рис. 7, I), то после скручивания эти образующие принимают вид винтовых линий, а каждое поперечное сечение по отношению к соседнему повора­чивается на некоторый угол (см. рис. 7, II). Это значит, что в каждом сечении происходит деформация сдвига и возникают касательные на­пряжения. Степень смещения материала при кручении определяется уг­лами закручивания Ө и сдвига γ. Абсолютная величина кручения опре­деляется углом закручивания рассматриваемого сечения Рис. 7

относительно неподвижно закрепленного сечения. Наибольший угол закручивания получается на самом большом расстоянии от закрепленного конца стержня.

Испытание на твердость. При опре­делении твердости материалов в завод­ской и лабораторной практике пользу­ются двумя методами: методом Бринелля и методом Роквелла.

Метод Бринелля. Этот метод основан на том, что при измерении твердости металлов стальной шарик 1 диаметром 2,5; 5 или 10 мм вдавливает­ся в поверхность испытуемого образца 2 при заданной нагрузке 3 от 625 Н до 30 кН (62,5 до 3000 кгс). После удаления нагрузки измеряется диаметр d отпе­чатка, оставшегося на поверхности об­разца (рис. 8), который тем меньше, чем тверже металл.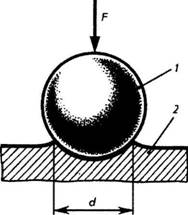



Рис. 8

Примечание. Стальной шарик должен быть выполнен из термически обрабо­танной стали твердостью не менее НВ850. Шероховатость поверхности R_z не ни­же параметра 0,100 по ГОСТ 2789-73. На поверхности шарика не должно быть де­фектов, видимых с помощью лупы при 5-кратном увеличении.

Число твердости по Бринеллю вычисляются по формуле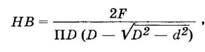



F — нагрузка на шарик, Н(кгс);

D — диаметр шарика, мм;

d — диаметр отпечатка, мм.

Специальная таблица (ГОСТ 9012-59) дает возможность определить твер­дость наиболее распространенных металлов.

Следует отметить, что между твердостью стали по Бринеллю НВ и преде­лом ее прочности о_пч для обычных углеродистых стилей существует соот­ношение, выраженное формулой о_пч = 0,36 НВ.

Следовательно, зная твердость стали по Бринеллю, можно вычислить и предел прочности при растяжении.

Эта формула имеет большое практическое значение. Методом Бринел­ля обычно определяют твердость незакаленных сталей, чугуна, цветных металлов. Твердость же закаленных сталей измеряют на приборе Рок­велла.

Метод Роквелла. При измерении твердости металлов наконечник стандартного типа (алмазный конус для твердых ме­таллов или стальной шарик — для более мягких), вдавливается в испыту­емый образец под действием двух последовательно прилагаемых нагру­зок. Первоначальной, (F₀) 100 Н (10 кгс) и окончательной (F₁) 1000 Н (100 кгс) — для шарика и 1500 Н (150 кгс) — для алмазного конуса.

Под действием предварительной нагрузки конус проникает в металл на глубину h₀ (рис. 9,I); при добавлении к предварительной основной нагруз­ки глубина отпечатка увеличивается до h (рис. 9, II) и после снятия основ­ной нагрузки остается равной h₁ (рис. 9, III).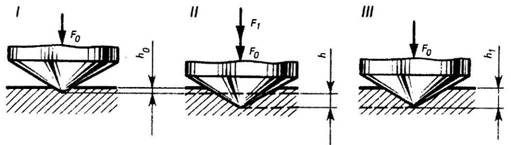



Рис. 9

Глубина отпечатка h = h₁ — h₀, полученная за счет основной нагрузки F₁, характеризует твердость по Роквеллу. Испытания по методу Роквелла производят специальными приборами, снабженными индикатором, который показывает число твердости сразу по окончании испытания.

Индикатор имеет две шкалы: черную (С) для испытания алмазным кону­сом и красную (В) для испытания шариком.

Твердость по Роквеллу измеряется в условных единицах.

Пример обозначения твердости по Роквеллу: HRC50 (твердость 50 по шкале С).

Определение твердости тарированными на­пильниками. Твердость HRC может быть определена с помощью ряда напильников, подвергнутых термической обработке на различную твер­дость насечки. Обычно интервал насечек колеблется от 3 до 5 единиц HRC. Тарирование напильников производится по эталонным плиткам, твердость которых заранее точно определена на приборе.

Твердость испытуемой детали определяется двумя напильниками с ми­нимальным интервалом по твердости, один из которых может только сколь­зить по детали, а второй ее слегка царапать. Если напильник с НRС62 цара­пает металл, а с HRC59 только скользит по поверхности детали, то твер­дость HRC60—61.

Практически этим способом пользуются для установления твердости ин­струментов (разверток, фрез и т. п.), твердость которых измерить иным спо­собом бывает трудно.

Метод измерения твердости по Виккерсу заключается во вдавливании в испытываемый материал правильный четырехгранной алмазной пирамиды с углом в 136° между противоположными гранями. Число твердости по Виккерсу вычисляется путем деления нагрузки на площадь поверхности пирамидального отпечатка. Обычно используют таблицы, с помощью которых по длине диагонали отпечатка находят число твердости. Если при измерении твердости используется нагрузка F = 30 кгс и время выдержки 10 … 15 с, твердость обозначается буквами HV и цифрами, характеризующими число твердости. Например, HV300, где HV – твердость по Виккерсу, 300 – число твердости в кгс/мм². При иных режимах измерения после символа HV указывают цифры, разделенные наклонной чертой и обозначающие нагрузку и время выдержки, а через тире – число твердости. Например, HV30/ 20 – 300, где HV – твердость по Виккерсу; 30 – нагрузка в кгс; 20 – время выдержки, с; 300 – число твердости. Почти полное совпадение значений твердости по Виккерсу и Бринеллю наблюдается в интервале 100 … 450 НВ.

Метод Виккерса широко применяется для определения твердости тонких образцов и тонких поверхностных слоев металла после химико-термической обработки, а также мелких деталей, деталей сложной формы.

Экспериментально установлено, что по значению твердости можно оценить предел прочности при растяжении σ_ut, условный предел текучести σ_0,2, модуль упругости Е материала. Так, для конструкционных углеродистых сталей с НВ ≥ 150, σ_0,2 ≈ 0,2 НВ и σ_ut ≈ 0,345 НВ; для латуни σ_ut ≈ 0,5 НВ; для дюралюминия σ_ut ≈ (0,36 … 0,37)НВ и т.д.