МПТ. Общие теоретические сведения Основы цифрового представления изображений
 Скачать 0.8 Mb. Скачать 0.8 Mb.
|
1 2 Написать программу, выполняющую следующие операции над изображениями (обязательна обработка как цветных, так и полутоновых изображений): Загрузить и отобразить изображение на экране. Реализовать возможность сохранения и вывода на экран обработанного изображения. Вывести гистограмму яркости изображения. Выполнить поэлементную обработку изображения в соответствии с вариантом, выданным преподавателем. Вывести гистограмму яркости обработанного изображения. Выполнить фильтрацию изображения (либо иной пространственный процесс) в соответствии с вариантом, выданным преподавателем. Вывести гистограмму яркости обработанного изображения. ЧАСТЬ 2 Выбрать одну из своих фотографий (изображение студента на данной фотографии приветствуется), которая требует определенной обработки (например, изменения контраста, яркости и т.д.), выполнить данную обработку. Показать преподавателю исходную фотографию, результат, обосновать необходимость определенной обработки, пояснить алгоритм. Можно использовать один из алгоритмов, приведенный в методичке, либо иной, но в рамках тематики лабораторной работы. Примечание: Варианты для выполнения лабораторной работы выдается преподавателем. Варианты поэлементной обработки и фильтрации (либо иного пространственного процесса) могут не совпадать. КЛАСТЕРНЫЙ АНАЛИЗ В РАСПОЗНАВАНИИ ОБРАЗОВ Каждый физический объект обладает набором некоторых свойств, которые позволяют отличить его от других объектов (рис. 2.1).  Рис. 2.1. Различные объекты Совокупность свойств, описывающих конкретный объект, называется образом данного объекта. Под классом объектов понимается некоторая совокупность образов, называемых элементами класса, обладающая рядом близких свойств. Измеряемые или вычисляемые свойства объектов, позволяющие отличить классы друг от друга, называются признаками. Так на изображении объекты (области) можно отличить, используя следующие признаки: Текстурные признаки; Геометрические признаки; Фотометрические признаки и др. Геометрические признаки Для каждой области можно подсчитать некий набор простейших числовых характеристик: Площадь; Центр масс; Периметр; Компактность; Ориентацию главной оси инерции; Удлиненность (эксцентриситет). На основе этих характеристик можно классифицировать получаемые объекты (области). Площадь – количество пикселей в области (рис. 2.2).  Рис. 2.2. Площадь объекта 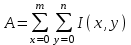 . (2.1) . (2.1)Центр масс 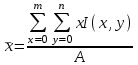 , , 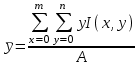 . (2.2) . (2.2)Периметр – количество пикселей, принадлежащих границе области (рис. 2.3).  Рис. 2.3. Периметр объекта Периметр зависит от того, какую связность (4-х или 8-ми) используют при определении соседей. Также отличают внутреннюю и внешнюю границу объекта (рис. 2.4). 1. Пиксель лежит на границе области, если он сам принадлежит области, а хотя бы один из его соседей области не принадлежит (внутренняя граница). 2. Пиксель лежит на границе области, если он сам не принадлежит области, а хотя бы один из его соседей области принадлежит (внешняя граница). 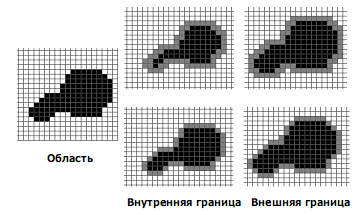 Рис. 2.4. Граница объекта Для распознавания, как правило, интересуют признаки, инвариантные к изменениям масштаба, переносу и повороту. Такими признаками являются удлиненность и компактность. Компактность – отношение квадрата периметра к площади (рис. 2.5): 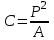 . (2.3) . (2.3)Наиболее компактная фигура – круг: 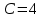 π. π.
Рис. 2.5. Компактность фигуры Дискретный центральный момент 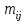 области определяется следующим образом: области определяется следующим образом: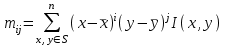 , (2.4) , (2.4)где 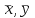 – центр масс области. – центр масс области.Удлиненность, нецентрированность (компактность) (рис. 2.6): 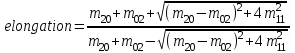 . (2.5) . (2.5)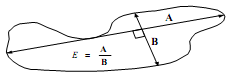 Рис. 2.6. Удлиненность фигуры Ориентация главной оси инерции не является инвариантной к повороту, но в ряде случаев предоставляет полезную информацию об ориентации объекта (рис. 2.7): 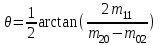 . (2.6) . (2.6)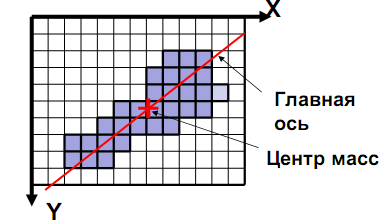 Рис. 2.7. Ориентация главной оси инерции объекта Фотометрические признаки Для каждой области можно подсчитать некий набор простейших числовых характеристик: Средняя яркость; Средний цвет (для цветного изображения); Гистограмма распределения яркостей (или для цветного изображения три гистограммы R, G, B); Дисперсия (разброс) яркости или цвета. Кластерный анализ Пусть число признаков равно n, тогда каждый образ можно представить в виде некоторого набора значений признаков или вектора признаков вида: 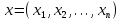 , (2.7) , (2.7)где 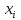 – значение i-го признака данного образа. – значение i-го признака данного образа.В многомерном пространстве, осями координат которого являются отдельные признаки, каждый образ определяется точкой, причем расстояние от этой точки до начала координат и расстояние между точками определяется выбранной метрикой. Каждый класс может характеризоваться некоторой областью в n-мерном пространстве признаков. Эта область определяется степенью отличия образов, относящихся к данному классу, и может задаваться границами, например плоскостями. Область, в которую с наибольшей вероятностью попадают векторы образов данного класса, обычно называют кластером, а процедуру разбиения пространства признаков на области, соответствующие разным классам, – кластеризацией совокупности образов. Если образы, относящиеся к одному классу, имеют различные значения признаков, то для описания класса можно использовать статистические характеристики: вектор средних значений или вектор математических ожиданий по всем признакам и вектор среднеквадратичных отклонений или дисперсий признаков. Для многомерных векторов принято использовать матрицу ковариации, на диагонали которой находятся дисперсии соответствующих признаков. Статистические характеристики признаков класса вычисляются следующим образом. Пусть набор n-мерных векторов, полученных в результате предъявления распознающей системе m объектов, относящихся к одному классу, задан в виде таблицы
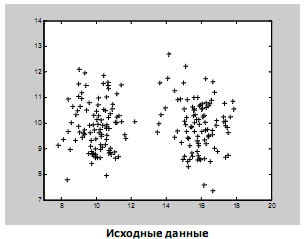
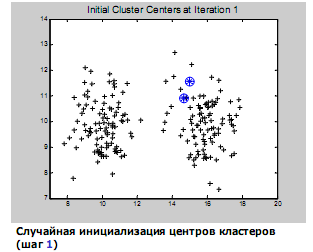
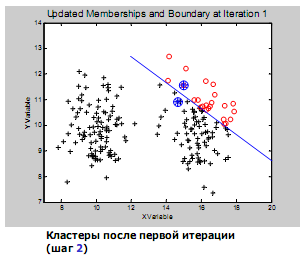
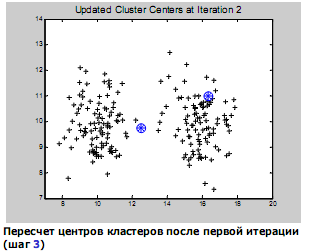
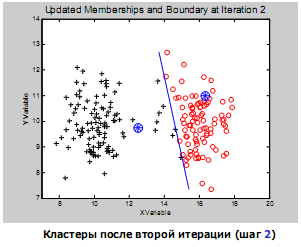
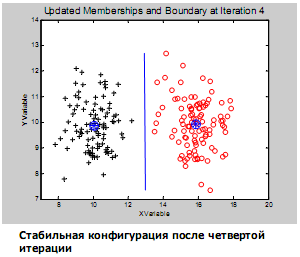
тогда m=(µ1, µ2,…,µn) : µi 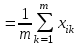 . (2.9) . (2.9)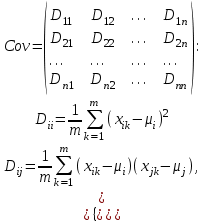 (2.10) (2.10)где i, j =1,…,n – индексы номеров компонент вектора признаков; m – число образов, составляющих данный класс; 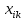 – значение i-го признака k-го образа; µi - математическое ожидание i-ой компоненты вектора признаков; – значение i-го признака k-го образа; µi - математическое ожидание i-ой компоненты вектора признаков; 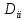 – дисперсия i-го признака; – дисперсия i-го признака; 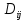 - коэффициент ковариации i-го и j-го признаков; m – вектор математических ожиданий; Cov – ковариационная матрица. - коэффициент ковариации i-го и j-го признаков; m – вектор математических ожиданий; Cov – ковариационная матрица. Ковариационная матрица симметрична относительно главной диагонали и, следовательно, необходимо вычислять только половину ее элементов. Ковариация характеризует степень линейной зависимости случайных величин. Если ковариация равна нулю, то величины называются некоррелированными. Таким образом, процесс распознавания включает в себя этап обучения, т.е. определения некоторых характеристик по обучающей репрезентативной выборке образов, отнесенных к известным классам, и собственно распознавание на основе информации, полученной при обучении. Под распознаванием образа понимается отнесение его к тому классу, расстояние до которого от данного образа в пространстве признаков минимально. Для определения расстояния между точками в метрическом пространстве признаков ранее было введено понятие метрики. Методы распознавания можно разделить на две группы. К первой группе относятся методы, основанные на последовательном вычислении расстояний между распознаваемым образом и центрами кластеров в пространстве признаков с той или иной метрикой, например Евклидово расстояние. Образ считается принадлежащим классу, расстояние до которого минимально. Другая группа методов предполагает предварительное разбиение признакового пространства плоскостями или поверхностями более высокого порядка на области, соответствующие известным классам, и определение принадлежности распознаваемого образа одной из областей. Выбор конкретного метода зависит от решаемой задачи. Существует около 100 разных алгоритмов кластеризации, однако чаще используется иерархический кластерный анализ и кластеризация методом k-средних. Остановимся подробнее на последнем. Алгоритм k-средних Метод k-средних – метод кластеризации данных. Целю задачи кластеризации является разбиение множества объектов на кластеры (классы) на основе некоторой меры сходства объектов. Дано: Набор векторов 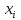 , i = 1,…, p; , i = 1,…, p;k – число кластеров, на которые нужно разбить набор 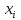 . .Найти: k средних векторов mj, j = 1,…, k (центров кластеров); отнести каждый из векторов 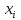 к одному из k кластеров; к одному из k кластеров;Алгоритм: 1. Случайным образом выбрать k средних mj j = 1,…, k; 2. Для каждого xi i = 1,…,p подсчитать расстояние до каждого из mj j=1,…, k, Отнести (приписать) xi к кластеру j’, расстояние до центра которого mj’ минимально; 3. Пересчитать средние mj j=1,…, k по всем кластерам; 4. Повторять шаги 2, 3, пока кластеры не перестанут изменяться. Пример кластеризации в 2D.
 Рис. 2.6. Примеры тестовых изображений Литература 1. Яне, Б. Цифровая обработка изображений / Б. Яне. – М. : Техносфера, 2007. 2. Гонсалес, Р. Цифровая обработка изображений / Р. Гонсалес, Р. Вудс. – М. : Техносфера, 2006. 3. Дуда, Р. Распознавание образов и анализ сцен / Р. Дуда, П. Харт. – М. : Мир, 1976. 4. Павлидис, Т. Алгоритмы машинной графики и обработки изображений / Т. Павлидис. – М. : Радио и связь, 1986. 5. Прэтт, У. Цифровая обработка изображений. В 2 т. / У. Прэтт. – М. : Мир, 1982. 1 2 |