вв. контр.работа для 1,2,3 темы (1). Общие вопросы теории цепей Электрическая цепь

• Название: Общие вопросы теории цепей Электрическая цепь
• Дата: 18.02.2023
• Размер: 1.85 Mb.
• Имя файла: контр.работа для 1,2,3 темы (1).doc
• Тип: Документы; #943843
• страница: 2 из 5

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Для правильного решения поставленной задачи необходимо изучить теорию электрических цепей однофазного синусоидального тока, усвоить основные формулы сопротивлений, проводимостей токов, напряжений; научиться применять для анализа и расчета закон Ома, уравнения Кирхгофа, метод проводимостей.

Все предлагаемые заданием электрические цепи являются смешанными, т.е. содержат последовательную ветвь и две параллельные. В каждой ветви имеются различные сопротивления, величины которых заданы.

Для примера рассмотрим обобщенную цепь, представленную на рис. 1.

ВНИМАНИЕ: РАСЧЕТ В ПРИМЕРЕ ДАЕТСЯ ТОЛЬКО ДЛЯ ЦЕПИ РИС.1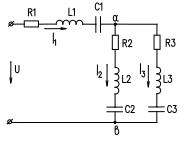



Общий ход решения задач подобного типа следующий. Необходимо преобразовать последовательно-параллельную цепь в простую последовательную цепь, заменив разветвленный участок цепи эквивалентной последовательной цепочкой.

Рис.1
Прежде всего, необходимо методом проводимости определить параметры эквивалентной цепочки, которой может быть замещен разветвленный участок цепи.

В эквивалентной цепочке реактивное сопротивление будет индуктивным или емкостным в зависимости от знака эквивалентной реактивной проводимости. Дальнейшее решение сводится к определению активного и реактивного сопротивления цепи, а по ним полного сопротивления цепи.

По каждому сопротивлению цепи и заданному напряжению определяется общий потребляемый ток в цепи. Чтобы определить ток в отдельных ветвях разветвленного участка, находим сначала напряжение между узловыми точками, а затем и токи в ветвях.

6

После чего находим напряжение на указанном участке, активную, реактивную и полную мощности в цепи. Заканчиваем расчет построением векторной диаграммы токов и напряжений.

Алгоритм расчета

1. 
   Вычисляем величины сопротивлений отдельных элементов цепи:
   

X_L = ω∙L = 2πf∙L,X_C = 1/ω∙C = 1/ 2πf∙C

где f = 50 Гц, L – в Генри (Гн), С – в Фарадах (Ф).

ВНИМАНИЕ: в задании L дается в мГн, С – в мкФ.

2. 
   Вычисляем полные сопротивления ветвей:
   

Z₁ = , где: X₁ = X_L1 – X_C1

Z₂ = ,X₂ = X_L2 – X_C2

Z₃ = ,X₃ = X_L3 – X_C3

3. 
   Вычисляем активные проводимости параллельных ветвей:
   

g₂ = R₂ / Z₂² ,g₃ = R₃ / Z₃² .

4. Вычисляем общую эквивалентную активную проводимостьg_Э:

g_Э = g₂ +g₃ .

5. 
   Вычисляем реактивные проводимости ветвей и общую эквивалентную проводимость G_Э :
   

в_L2 = X_L2/ Z₂² ,в_C2= X_C2 / Z₂² ,

в_L3 = X_L3 / Z₃² ,в_C3 = X_C3 / Z₃² ,G_Э =

в_L =в_L2 + в_L3 ,в_C = в_C2 + в_C3 ,в_Э = в_C– в_L .

5. 
   Изобразим эквивалентную схему, на которой сопротивления заменим проводимостями (рис.2).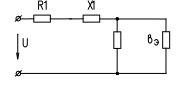
   

g_Э

Рис.2

5. 
   Заменим эквивалентные проводимости эквивалентными сопротивлениями, включенными последовательно (рис.3).
   

7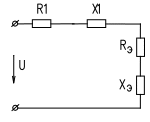

R_Э = g_Э / G_Э ²

X_Э = в_Э / G_Э ²

Рис.3

5. 
   Найдем общее сопротивление всей цепи:
   

R_Ц = R₁ + R_Э ,X_Ц = X₁ + X_Э, Z_Ц = , Ом.

5. 
   Найдем общий потребляемый ток:
   

I₁ = U / Z_Ц, A .

5. 
   Найдем напряжение, приложенное к параллельному участку цепи:
   

U_ав = I₁· Z_Э , В;Z_Э = 1 / G_Э .

5. 
   Найдем токи в ветвях:
   

I₂ = U_ав/ Z₂ , А; I₃ = U_ав/ Z₃ , А .

5. 
   Найдем напряжение на сопротивлении Z₁ :
   

U_Z1 = I₁·Z₁ , В .

5. 
   Вычисляем мощности цепи:
   

P = U·I₁·cosφ, Вт; Q = U·I₁·sinφ, ВАр; S = U·I₁, В·А, где cosφ= R_Ц / Z_Ц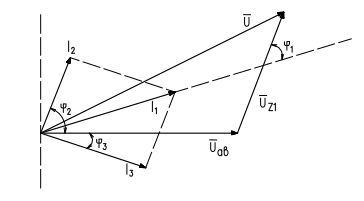

5. 
   Строим векторную диаграмму токов и напряжений, предварительно определив масштаб для векторов напряжений и векторов тока (рис.4).
   

8
Рис.4

В качестве исходного вектора удобно принимать вектор напряжения, приложенного к параллельным ветвям, вектор U_ав .

Откладываем вектор U_ав . Относительно этого вектора откладываем в масштабе тока токи I₂ и I₃, определив вначале углы сдвига по фазе φ₂ и φ₃ ;

(cosφ₁ = R₁ / Z₁ ; cosφ₂ = R₂ / Z₂; cosφ₃ = R₃ / Z₃ ).

Токи откладываем в сторону отставания или опережения, что определяется характером нагрузки в параллельных ветвях.

Произведем геометрическое сложение, находим ток I₁: (I₁ =I₂ + I₃).

Относительно вектора тока I₁ под углом φ₁ в сторону опережения или отставания, что определяется характером нагрузки r , X_L , X_C , откладываем вектор U_Z , из конца вектора U_ав . Геометрическим сложением этих векторов (U = U_ав + U_Z1 ) находим вектор напряжения U.

9