Оценка связи между качественными признаками. Оценка связи между качественными признаками
 Скачать 202.97 Kb. Скачать 202.97 Kb.
|
|
| ^^^-^Г1ризнаки Группы | 1 | 2 | Сумма |
| 1 | а | Ь | а + b |
| 2 | с | d | с + d |
| Сумма | а + с | b + d | Г |
Этими полями являются клетки а, b, с, d.
Расчет осуществляется на основе сопряжения по строкам а и Ь, с и d, а также по графам awc.bwd. Формула расчета:
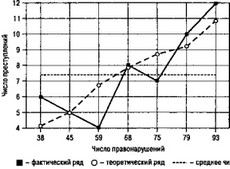
Ассоциируемые показатели могут быть как абсолютными, так и относительными. Попробуем рассчитать КП между показателями раненых и погибших в дорожно-транспортных происшествиях по вине водителей и пешеходов (табл. 2).
Ввиду того, что абсолютные показатели громоздки и расчет КП на их основе можно сделать будет только на компьютере, исчислим его на относительных показателях, на процентах:
Распределение погибших и раненых по вине водителей и пешеходов
Таблица 2
| Причина наезда | Погибло | Ранено | Сумма |
| Вина водителей | {а) | (Ь) | |
| | 26 807 | 146 685 | 173 492 |
| | (15,5%) | (84,5%) | (100,0%) |
| Вина пешеходов | (с) | (d) | |
| | 6451 | 40 293 | 46 784 |
| | (13,8%) | (86,2%) | (100,0%) |
| Сумма | 33 258 | 186 978 | — |
| | (29,3%) | (170,7%) | |
Проверка расчета КП на абсолютных показателях дала практически те же результаты (0,0188). Расхождение расчетов на десятитысячные доли объясняется наличием округлений при расчете процентов.
Коэффициент ассоциации измеряется от -1 до + 1 и интерпретируется так: чем ближе коэффициент к 1, тем теснее связь, положительная или отрицательная. Исходя из этого связь между показателями раненых и погибших по вине водителей и пешеходов прямая (+), но незначительная и случайная. Считается, что если КП достигает 0,3, то это свидетельствует о существенной связи между признаками. Коэффициент взаимной сопряженности, разработанный отечественным статистиком А.А. Чупровым (КЧ), в отличие от коэффициента Пирсона применяется для измерения связи между соотношением двух
атрибутивных признаков по трем и более группам. Он рассчитывается по формуле
alt="" />, где КЧ — коэффициент взаимной сопряженности А.А. Чулрова; ср — показатель взаимного сопряжения (фи квадрат); т] и т2 — число групп по каждому признаку; 1 — постоянный коэффициент.
Поскольку число групп всегда известно, то для расчета КЧ необходимо найти ф2 (фи квадрат). Его расчет сложный. Он, как и коэффициент Пирсона, исчисляется путем нахождения различных соотношений, что легче всего сделать на конкретном примере. В качестве такового возьмем соотношение некоторых видов преступлений и их раскрываемости (табл. 3). В нашем примере т { — число видов деяний, равное 4, и т2 — число групп по раскрываемости преступлений (раскрыты, нераскрыты), равное 2.
Таблица 3
Распределение некоторых преступлений в регионе по видам и их раскрываемости
| Виды преступлений | Раскрыты | Не раскрыты | Итого |
| Разбой | 110 (73,7%) 12 100 34,5714 | 40 (26,3%) 1600 10,6667 | 150 (100%) 45,2381 0,3016 |
| Мошенничество | 180 (73,5%) 32 400 92,5714 | 65 (26,5%) 4225 28,1667 | 245 (100%) 120,7381 0,4928 |
| Умышленное убийство | 50 (66,7%) 2500 7,1429 | 25 (33,3%) 625 4,1667 | 75 (100%) 11,3096 0,1508 |
| Поджог | 10 (33,3%) 100 0,2857 | 20 (66,7%) 400 2,6667 | 30 (100%) 2,9524 0,0984 |
| Итого | 350 | 150 | 500 1,0436 |
Для того чтобы разобраться в этой таблице, раскроем значение каждого показателя и способы его получения на примере разбоев, v В первой строке каждой клетки (кроме итоговой графы) указаны абсолютные числа и удельные веса (в скобках) раскрытых и нераскрытых преступлений (разбой, мошенничество и т.д.).
Применительно к разбоям: раскрыто 110 деяний, или 73,7%, и не раскрыто 40, или 26,3%.
Во второй строке каждой клетки (кроме итоговой графы) указаны квадраты частот преступлений. Применительно к разбоям: ПО раскрытых деяний в квадрате составляет 12 100, а 40 нераскрытых в квадрате составляет 1600.
В третьей строке каждой клетки (кроме итоговой графы) указаны частные от деления квадратов частот на сумму частот по графам (эти суммы указаны в нижней строчке «Итого»). Применительно к раскрытым разбоям: 12 100 : 350 = 34,5714 и применительно к нераскрытым: 1600 : 150 = 10,6667.
Каждая клетка итоговой графы состоит из четырех строк:
в первой строке даны суммы частот и частостей (110 раскрытых разбоев + 40 нераскрытых = 150, или 100%);
во второй строке — прочерк, так как квадраты частот не суммируются;
в третьей строке даны суммы частных от деления квадратов частот на суммы частот раскрытых и нераскрытых деяний, применительно к разбою: 34,5714 (раскрытые) + 10,6667 (нераскрытые) = 45,2381;
в четвертой строке дается отношение сумм частных (указанных в предыдущей третьей строке) к общему числу частот (указанных в первых строках каждой клетки), применительно к разбою 45,2381 : 150 = = 0,316.
В итоговой строке итоговой графы приводятся два числа: первое общее число частот (500 преступлений) и второе — общая сумма отношений, указанных в четвертой строке предыдущих клеток итоговой графы (0,3016 + 0,4928 + 0,1508 + 0,984 = 1,0436).
Результирующее число 1,0436, вобравшее в себя все статистически значимые отношения, за вычетом единицы, т.е. 1,0436 - 1 == 0,0436, является именно фи квадратом (lt;р2), указывающим на взаимную сопряженность атрибутивных признаков нескольких групп. Имея его, мы легко рассчитаем КЧ по предложенной формуле:
Коэффициент А.А. Чупрова в отличие от коэффициента ассоциации варьирует от 0 до 1. Если исходить из формулы, то его значение не может быть отрицательным.
Но суть интерпретации та же. Связь считается существенной при величине КЧ = 0,3. Чем ближе его значение к единице, тем сильнее связь. КЧ = 0,16 — свидетельство наличия относительно заметной связи между видами преступлений и их раскрываемостью. Особая роль в выявлении связей не только между качественными, но и количественными признаками принадлежит параллельным статистическим рядам. С одной стороны, они представляют собой относительно самостоятельный и важный метод выявления корреляционной зависимости, с другой — с их сопоставления начинается расчет однофакторных, многофакторных и иных корреляций.
Параллельные ряды в этом смысле представляют собой сопоставление двух и более статистических вариационных или динамических рядов показателей, причинно или иным способом связанных между собой. Они дают возможность не только увидеть изменения одного явления в рядах распределения или динамики, но и установить взаимосвязанное изменение двух или более явлений.
Обратимся к известному примеру о связи пьянства с преступностью. Сопоставив за несколько лет два динамических ряда,(число преступлений и количество потребления алкоголя в литрах на 100 тыс. населения), мы можем выявить наличие и характер связи между ними. Связь прямая и достаточно сильная, хотя и неодинаковая по силе и механизму действия при совершении различных видов преступлений.
Корыстные преступления совершаются с целью добычи денег на приобретение спиртного; насильственные действия — вследствие снятия нравственно-правовых тормозов у субъектов, находящихся в состоянии опьянения; совершению легкомысленных (неосторожных) деяний, например дорожно-транспортных, способствует ослабление реакции и другие воздействия алкогольного опьянения на психическое и физическое состояние субъектов преступления[CXXVI].
Существующие взаимосвязи между пьянством и преступностью в нашей стране особо четко проявились в последние 10—15 лет, когда в середине 80-х гг. пьянство интенсивно росло; когда в 1986—1987 гг. прошла кампания ожесточенной борьбы с пьянством и алкоголизмом, когда в процессе распада Союза и непродуманных реформ в России был снят государственный контроль за производством и оборотом алкогольных напитков.
Все это наглядно отразилось на динамике преступности в целом и ее отдельных групп и видов. В 1983—1985 гг. уровень преступности интенсивно рос, в 1986—1987 гг. — заметно снижался, а в 1988—1990 гг. рост преступности был беспрецедентным. Между потреблением алкогольных напитков и преступностью существует прямая сильная связь причинного характера (рис. 35).
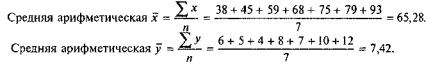
Рис. 1. Динамика преступлений и потребления алкоголя в России (1983—1990 гг.)
Параллельные ряды в юридической статистике применимы также для сопоставления рядов динамики преступности и раскрываемости, преступности и выявленных правонарушителей, преступности и судимости, преступности, судимости и числа заключенных. Эти ряды могут свидетельствовать о результативности борьбы с преступностью, степени соответствия судебной практики криминогенным тенденциям, месте и роли лишения свободы в борьбе с преступностью и т.д. Обратимся еще раз к динамическим рядам уровней преступности и выявленных правонарушителей (рис. 36).
Между уровнем преступности и выявленными правонарушителями существует связь состояний. И преступность, и выявленные правонарушители имеют одни и те же причины. Выявленные правонарушители по сути своей — раскрытая часть учтенной преступности. Но на динамику уровня выявленных правонарушителей влияют и другие факторы: уголовная политика, степень соблюдения презумпции невиновности, дееспособность правоохранительных органов и др.
Мы обращались к этим данным. В 1956 г. число выявленных правонарушителей было на 29% больше числа учтенных преступлений, в 1972 .г. их уровни сравнялись, а в 1991 г. число учтенных преступлений на 54% превышало число выявленных правонарушителей. Анализ этих парадоксальных соотношений между уровнями преступности и выявленных правонарушителей может дать ответы на очень сложные во
просы уголовной политики в нашей стране за последнее пятидесяти- летие.
Любые показатели о юридически значимых явлениях могут быть поставлены в параллельные статистические ряды распределения и динамики, если между ними существуют реальные причинные или иные связи. Однако обнаруженные совпадения |иогут быть случайными или ложными. В одном исследовании 60-х гг. утверждалось, что рождаемость находится в прямой зависимости от размера жилплощади: чем больше площадь, тем выше рождаемость. В другом говорилось обратное: чем теснее живут, тем выше рождаемость, так как получение большей жилплощади прямо зависело от количества детей. В обоих случаях мы имеем дело с ложными закономерностями.
Известный отечественный криминолог и статистик М.Н. Гернет, например, построил параллельные ряды осужденных в Калужской губернии за кражи (в расчете на 10 тыс. населения) и цен на хлеб (в копейках за пуд), чем, как он писал, доказал «полную зависимость между ценами на хлеб и числами осужденных окружным судом за кражи»1. Статистические совпадения указанных рядов объяснимы. Рост цен на хлеб может как-то отражать ухудшение экономической и криминоген-
Гернет М.Н. Избранные произведения. М., 1974. С 273.
ной ситуации. Но выявленные корреляции характеризуют, скорее всего, не связи между кражами и ценами на хлеб, а связи между кражами и экономической ситуацией в целом. Цена на хлеб в отдельно взятой губернии — лишь какой-то косвенный индикатор экономической ситуации. Подобные корреляции могут затушевать или искажать действительное положение дел. Случайность совпадений или ложные закономерности, как правило, выясняются на основе качественного анализа и теории той научной дисциплины, статистические данные которой анализируются.
Об этом образно писал Л.Н. Толстой в томе третьем части третьей романа «Война и мир»: «Всякий раз, когда я, глядя на свои часы, вижу, что стрелка подошла к десяти, я слышу, что в соседней церкви начинается Благовест, но из того, что всякий раз, что стрелка приходит на десять часов тогда, как начинается Благовест, я не имею права заключить, что положение стрелки есть причина движения колоколов. Всякий раз, как я вижу движение паровоза, я слышу звук свиста, вижу открытие клапана и движение колес; но из этого я не имею права заключить, что свист и движение колес суть причины движения паровоза.
Крестьяне говорят, что поздней весной дует холодный ветер, потому что почка дуба развертывается, и действительно всякую весну дует холодный ветер, когда развертывается дуб... Я вижу только совпадение тех условий, которые бывают во всяком жизненном явлении, и вижу, что, сколько бы и как бы подробно я ни наблюдал стрелку часов, клапан и колеса паровоза и почку дуба, я не узнаю причину Благовеста, движения паровоза и весеннего ветра. Для этого я должен изменить совершенно свою точку наблюдения и изучать законы движения пара, колокола и ветра»[CXXVII].
Параллельные ряды как метод выявления взаимосвязей используются давно. В работе «Население, преступность и пауперизм» Маркс, сопоставляя в параллельных рядах численность населения, родившихся, умерших, осужденных и пауперов, установил важную закономерность: преступность растет быстрее, чем численность населения[CXXVIII]. Со времени этого открытия прошло более ста лет, а выявленные закономерности действуют. По данным Четвертого обзора ООН о тенденциях преступности (1986—1990 гг.) преступность в мире прирастала на 5% в год, а население — около 1—1,5%.
Наличие параллельных рядов признака-фактора (х) и признака- следствия (у) позволяет выявить и изобразить корреляционные зависимости графически в прямоугольной системе координат.
Если отложить значения хна оси абсцисс, а значение у — на оси ординат и нанести точки соотношений х и у, то мы получим корреляционное поле, где по расположению точек можно судить о характере и степени связи (рис. 1).
Если точки беспорядочно разбросаны по всему полю (а), то какой- либо связи между признаками нет. Если они сосредоточены на оси, направленной снизу-вверх и слева направо (б), то имеется прямая зависимость, а если точки распределены сверху вниз и слева направо (в), то зависимость будет обратной. Если точки при прямой или обратной зависимости не расплываются в облаке, а сосредоточены на одной линии (г), то в этом случае мы имеем сильную прямую или обратную связь.
Взаимосвязь цепных и базисных индексов.
Индексы могут использоваться для анализа динамики социально-экономических явлений за некоторый интервал времени, включающий более двух периодов. В этом случае рассчитываются системы индексов.
Система индексов - это ряд последовательно построенных индексов, характеризующих изменения, происходящие в изучаемом явлении в течение исследуемого периода времени.
В зависимости от базы сравнения системы индексов бывают цепными и базисными.
Система базисных индексов - это ряд последовательно вычисленных индексов одного и того же явления с постоянной базой сравнения (т.е. в знаменателе всех индексов находится индексируемая величина базисного периода).
Система цепных индексов - это ряд индексов одного и того же явления, вычисленных с меняющейся от индекса к индексу базой сравнения.
Эти системы индексов могут быть построены для индивидуальных и общих индексов.
Так как индексы являются относительной величиной динамики, то они также могут быть базисными и цепными:
– базисные индексы получают сопоставлением с уровнем периода, принятого за базу сравнения, т.е. база сравнения, остаётся постоянной;
– цепные индексы получают сопоставлением текущих уровней с предшествующим, т.е. база сравнения непрерывно меняется.
Для индивидуальных индексов цен, физического объёма и стоимости продукции справедливо следующее правило:
1. Последовательное произведение цепных индексов даёт базисный индекс последнего периода:
2. Отношение базисного индекса отчётного периода к базисному индексу предшествующего периода даёт цепной индекс отчётного периода
и
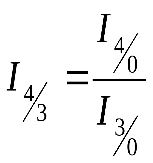 л
л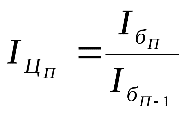 и
иЗадача 3.
Имеются следующие данные об изменении численности рабочих на заводе, в % к предыдущему году:
| 2007 | 2008 | 2009 | 2010 | 2011 |
| +5 | +4 | +7 | +5 | +6 |
Определить на сколько процентов увеличилось число рабочих на заводе за 5 лет, т.е. в 2011 году по сравнению с 2006 годом.
Решение.
+Зная, что базисный индекс можно получить путем перемножения цепных индексов, находим:
