метрлогия. КР метрология. Одержание
 Скачать 297.93 Kb. Скачать 297.93 Kb.
|
|
Задача 1. Определение предельных размеров замыкающего звена размерной цепи (т.е. точность этого звена), когда известны предельные размеры остальных составляющих звеньев. Эту задачу называют "проверочной", поскольку необходимость в ее решении возникает тогда, когда закончилось конструирование объекта и определилась его конструкция, т.е. известны значения всех составляющих звеньев и установлены требования к их точности. Необходимо определить, какое значение размера будет у замыкающего звена при тех предельных размерах, которые имеют составляющие звенья, и соберется ли сборочная единица при заданной точности составляющих звеньев. Задача 2. Определение предельных размеров составляющих звеньев размерной цепи, когда известны предельные размеры замыкающего звена и номинальные значения размеров составляющих звеньев. При решении этой задачи замыкающее звено обычно называют "исходным звеном". Эту задачу называют "проектировочной", поскольку решать ее приходится при проектировании конструкции. Так, после того как определилась конструкция сборочной единицы или механизма и габаритные размеры всех деталей (стали известны номинальные размеры), а также стали известны требования к точности замыкающего (исходного) звена. Например, известен необходимый зазор при сборке размерной цепи, требуется нормировать точность составляющих звеньев (задать на них отклонения от номинала), чтобы при сборке была обеспечена точность требуемого зазора (размер исходного замыкающего звена). Методы достижения заданной точности исходного звена. Существуют следующие методы достижения заданной точности исходного звена (решения размерных цепей): 1. Метод полной взаимозаменяемости (максимума – минимума). 2. Теоретико-вероятностный метод. 3. Метод групповой взаимозаменяемости. 4. Метод регулирования. 5. Метод пригонки. 1. Метод полной взаимозаменяемости. Характеристика. Детали соединяются на сборке без дополнительных операций. Значения замыкающего звена не выходят за установленные пределы. Расчет размерной цепи производится методом максимума – минимума. Преимущества. Простота и экономичность сборки; упрощение организации поточного сборочного процесса; возможность широкого кооперирования. Недостатки. Допуски составляющих звеньев получаются наименьшими из всех методов, что может оказаться неэкономичным. Область применения. В индивидуальном и мелкосерийном производстве, при большей величине допуска на исходное звено и малом числе составляющих звеньев. Если применение этих методов экономически нецелесообразно или технически невозможно, следует перейти к использованию одного из методов неполной взаимозаменяемости. При выборе метода расчета цепей можно ориентироваться на среднюю величину допуска составляющих звеньев или среднюю степень точности (квалитет) составляющих звеньев. 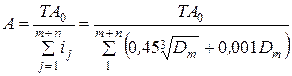 (2) (2)Метод полной взаимозаменяемости. После составления уравнения размерной цепи и решения его относительно  (3) (3)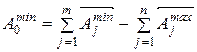 (4) (4)Вычитая почленно из (3) выражение (4) получим формулу для определения допуска замыкающего звена: 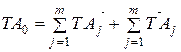 (5) (5)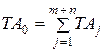 (6) (6)Анализируя формулу (6) можно сделать следующие выводы: 1. В качестве замыкающего звена при сборке или изготовлении необходимо принимать наименее ответственный размер. 2. Точность замыкающего звена увеличивается с уменьшением допусков составляющих звеньев. 3. Сокращение числа звеньев приводит к повышению точности замыкающего звена; чем меньше число составляющих, тем больше допуски на составляющие звенья при той же величине допуска на исходное (замыкающее) звено, тем меньше стоимость изготовления. Если из уравнений (3) и (4) вычесть последовательно уравнение, получим выражения для определения предельных отклонений замыкающего (исходного) звена: При расчете размерных цепей часто оказывается удобным оперировать не предельными отклонениями ES и EI, а средними отклонениями Е РИСУНОК. Сложив почленно уравнения и учитывая получим среднее отклонение поля замыкающего звена. Решение прямой задачи. Такая задача встречается гораздо чаще. Она наиболее важна, поскольку конечная цель расчета допусков составляющих размеров при заданной точности сборки (заданном допуске исходного звена) – обеспечить выполнение машиной ее функционального назначения. Эту задачу можно решать одним из следующих способов. 59. Основные сведения, термины и определения метрологии Основные термины и определения в области метрологии устанавливаются Рекомендациями по межгосударственной стандартизации РМГ29-99 «Метрология. Основные понятия и определения». Метрология — наука об измерениях физических величин, методах и средствах обеспечения их единства и способах достижения требуемой точности. Слово "метрология" образовано из двух греческих слов: «метрон» - мера и логос - учение. Дословный перевод слова "метрология" - учение о мерах. Долгое время метрология оставалась в основном описательной наукой о различных мерах и соотношениях между ними. С конца прошлого века благодаря прогрессу физических наук метрология получила существенное развитие. Большую роль в становлении современной метрологии как одной из наук физического цикла сыграл Д. И. Менделеев, руководивший отечественной метрологией в период 1892 - 1907 гг. Метрология, в ее современном понимании, - наука об измерениях, методах, средствах обеспечения их единства и способах достижения требуемой точности. Под единством измерений понимают такое состояние измерений, при котором их результаты выражены в стандартизированных единицах и погрешности измерений известны с заданной вероятностью. Единство измерений необходимо для того, чтобы можно было сопоставить результаты измерений, выполненных в разных местах, в разное время, с использованием разных методов и средств измерений. Точность измерений характеризуется близостью их результатов к истинному значению измеряемой величины. Так как абсолютно точных приборов не существует, то о точности приборов можно говорить лишь в терминах теории вероятности и математической статистики. Важнейшей задачей метрологии является усовершенствованием эталонов, разработкой новых методов точных измерений, обеспечение единства и необходимой точности измерений. Метрология включает в себя следующие разделы: 1. Теоретическая метрология, где рассматриваются общие вопросы теории измерения. 2. Прикладная метрология изучает вопросы практического применения результатов теоретических исследований 3. Законодательная метрология рассматривает комплекс правил, норм и требований регламентируемых государственными органами для обеспечения единства измерений и единообразия средств измерений. Под измерением понимают процесс получения количественной информации о значении какой-либо физической величины опытным путем с помощью средств измерения. Физическая величина - это свойство, общее в качественном отношении многим физическим объектам (системам, их состояниям и происходящим в них процессам), но в количественном отношении индивидуальное для каждого объекта. Единица физической величины - это физическая величина, размеру которой присвоено числовое значение 1. Размер физической величины - количественное содержание в данном объекте свойства, соответствующего понятию "физическая величина". Для каждой физической величины должна быть установлена единица измерения. Все физические величины связаны между собой зависимостями. Их совокупность можно рассматривать как систему физических величин. При этом если выбирать несколько физических величин за основные, то другие физические величины можно через них выразить. Все единицы измерения подразделяют на основные и производные (полученные из основных). Выражение, отражающие связь физической величины с основными физическими величинами системы называется размерностью физической величины. Основные представления теоретической метрологии. Физические величины и единицы. Согласно РМГ 22-99, физическая величина (ФВ) одно из свойств физического объекта, в качественном отношении общее для многих физических объектов, а в количественном отношении индивидуальное для каждого из них. Величина не существует сама по себе, она имеет место постольку поскольку существует объект со свойствами, выражаемыми определёнными величинами. Идеальные величины относятся главным образом к математическим абстракциям, являющимися отражением реальности. ФВ присущи материальным объектам и изучаются в курсах естественных (физика, химия) и технических наук. Нефизические величины изучаются в курсах общественных наук - философии, экономике и т.д. Физические объекты обладают неограниченным числом свойств, которые проявляются с бесконечным разнообразием, что вызывает затруднения в их отражении конечными совокупностями чисел, возникающими при их измерении. Отметим, что оценивание нефизических величин не входит в задачи теоретической метрологии. Для более детального изучения ФВ необходимо классифицировать и выявить общие метрологические особенности их отдельных групп. ФВ целесообразно разделить на измеряемые и оцениваемые. Если первые могут быть выражены количественно в виде определённого числа установленных единиц измерения, то для вторых в силу невозможности введения единицы измерения (твёрдость), приписываются величине определённое число по установленным правилам. Оценивание такой величины осуществляется при помощи шкал. Шкала величины Шкала величины - упорядоченная последовательность её значений, принятая по соглашению на основании результатов точных измерений. Нефизические величины могут быть только оценены. По видам явлений ФВ делятся на следующие группы: - вещественные, т.е. описывающие физические и физико-химические свойства веществ, материалов и изделий из них. К этой группе относятся масса, плотность, электрическое сопротивление и др. Иногда указанные ФВ называют пассивными. Для их измерения необходимо использовать вспомогательный источник энергии, с помощью которого формируется измерительный сигнал. При этом пассивные ФВ преобразуются в активные, которые и измеряются; - энергетические, т. е. величины, описывающие энергетические характеристики процессов преобразования, передачи и использования энергии. К ним относятся ток, напряжение, мощность, энергия. Эти величины называют активными. Они могут быть преобразованы в сигналы измерительной информации без использования вспомогательных источников энергии; - характеризующие протекание процессов во времени. К этой группе относятся различного рода спектральные характеристики, корреляционные функции и др. По принадлежности к различным группам физических процессов ФВ делятся на пространственно-временные, механические, тепловые, электрические и магнитные, акустические, световые, физико-химические, ионизирующих излучений, атомной и ядерной физики. По степени условной независимости от других величин данной группы·ФВ делятся на основные (условно независимые), производные (условно зависимые) и дополнительные. В настоящее время в системе СИ используется семь физических величин, выбранных в качестве основных: длина, время, масса, температура, сила электрического тока, сила света и количество вещества. К дополнительным физическим величинам относятся плоский и телесный углы. По наличию размерности ФВ делятся на размерные, т. е. имеющие размерность, и безразмерные. Совокупность чисел Q, отображающая различные по размеру однородные величины, должна быть совокупностью одинаково именованных чисел. Это именование является единицей ФВ или ее доли. Условно за единицу принимается физическая величина (ФВ) фиксированного размера, а результат может быть выражен в единицах ФВ или её долях. Для третьей группы числовое значение показывает, в каком соотношении значение измеряемой величины находится в сравнении с принятым за единицу. Измерение - познавательный процесс, заключающейся сравнении путём физического эксперимента данной ФВ с известной ФВ, принятой за единицу измерения. Шкалы измерений. В соответствии с логикой проявления свойств различают 5 основных типов шкал измерений. 1. Шкала наименований (шкала классификации). Такие шкалы используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности (атлас цветов). Эти свойства нельзя считать физическими величинами, поэтому это не шкалы ФВ. В шкалах наименований отнесение к классу эквивалентности того или иного отражаемого свойства происходит с использованием органов чувств человека и наиболее адекватен результат, выбранный большинством экспертов. Числа, приписанные объектам, могут быть используемы лишь для определения вероятности или частоты появления объекта, но для математических действий (например суммирования) эти числа использовать нельзя. В таких шкалах нет понятия нуля, “больше“ или “меньше“ и единицы измерения. 2. Шкала порядка (шкала рангов). Если свойство объекта проявляется в отношении эквивалентности и порядка, то можно построить шкалу. При этом в шкале может существовать 0 или нет, но принципиально нельзя ввести единицу измерения. В тех случаях, когда уровень познания не позволяет точно установить отношения, существующие между величинами данной характеристики, используют условные (эмпирические) шкалы порядка. Иногда использование такой шкалы удобно и достаточно для практики. Условная шкала - это шкала ФВ, исходные значения которой выражены в условных единицах (12-бальная шкала Бофорта для силы морского ветра). Широкое распространение получили шкалы порядка с реперными точками на них (например, шкала твёрдости Мооса). На ней принимается твёрдость талька за 1 (первая реперная точка), гипса за 2, и т.д., алмаза за 10. Отнесение минерала к той или иной градации твёрдости производится на основании эксперимента, когда исследуемый материал царапается опорным. Более твёрдый материал оставит след на образце, значит верхняя граница твёрдости не меньше твёрдости опорного материала. Нижняя граница определяется аналогично. В условных шкалах одинаковым интервалам между размерами данной величины не соответствуют одинаковые размерности чисел, отображающие размеры. Для вычисления вероятностей эти числа можно использовать, однако их нельзя использовать для других математических операций. Определение значения величин при помощи таких шкал нельзя считать измерением, т.к. как на такой шкале не может быть введена единица измерения. Это операция оценивания, неоднозначная и весьма условная. 3. Шкала интервалов (шкала разностей). Эта шкала применяется для объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности. Она состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. К таким шкалам относится летоисчисление по различным календарям, температурные шкалы Цельсия, Фаренгейта, Реомюра. На ней определены действия сложения, однако складывать даты событий, например, бессмысленно. Шкала интервалов величины Q описывается уравнением: Q = Q0 + q [Q],(11) где q - числовое значение величины; Q0 - начало отсчета шкалы; [Q] - единица рассматриваемой величины. Задать шкалу можно двумя способами. При первом выбирают два значения Q1 и Q0 - величины, называемые основные реперы, которые просто реализуются практически, а интервал (Q1 - Q0) - называется основной интервал. Точка Q0 принимается за начало отсчёта, а величина (Q1 - Q0)/n = [Q] - за единицу Q. Перевод одной шкалы интервалов Q = Q01 + q1[Q]1, в другую Q = Q02 + q2 [Q]2 осуществляется по формуле: q2 =(q1 – По второму пути единица воспроизводится как интервал, его доля или некоторое число интервалов, а начало отсчета выбирается каждый раз по - разному, в зависимости от конкретных условий изучаемого явления. Пример такого подхода - шкала времени., в которой секунда равна 9192631770 периодам излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия - 133. За начало отсчета принимается начало изучаемого явления. Шкала отношений. Эти шкалы описывают свойства эмпирических объектов, которые удовлетво-ряют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода - аддитивные), а иногда и пропорциональности (шкалы первого рода - пропорциональные). Примеры: шкала массы (второго рода), термодинамической температуры (первого рода). В шкалах отношений существует однозначный естественный критерий нуля и единица измерений, установленная по соглашению. Формально шкала отношений - это шкала интервалов с естественным началом отсчета. К значениям, полученным по этой шкале, применимы все арифметические действия, что имеет важное значение при измерении ФВ. Шкалы отношений - самые совершенные. Они описываются уравнением: Q = q [Q],(13) где Q - ФВ, для которой строится шкала, [Q] - ее единица измерения, q - числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением q2 = q1 [Q]1 /[Q]2.(14) Абсолютные шкалы. Иногда используют понятие абсолютных шкал, под которыми понимают шкалы, обладающие всеми признаками шкал отношений, но дополнительно имеющие естественное однозначное определение единицы измерения и не зависящее от принятой системы единиц измерения. Такие шкалы соответствуют относительным величинам: коэффициенту усиления и т.д. Для образования многих производных единиц в системе СИ используются безразмерные и счетные единицы абсолютных шкал. Шкалы наименований и порядка называют неметрическими (концептуальными), а шкалы интервалов и отношений - метрическими (материальными). Абсолютные и метрические шкалы относятся к разряду линейных. На практике шкалы измерений стандартизуются, также, как и единицы измерений. В необходимых случаях принимается стандарт способа и условий их однозначного воспроизведения. Во всех случаях проведения измерений, независимо от измеряемой величины, метода и средства измерений, общее, что составляет основу измерений - сравнение опытным путём данной величины с другой ей подобной, принятой за единицу. Это может быть записано в виде общего уравнения измерений: Q=n[Q],(15) где Q − измеряемая физическая величина; п − число единиц; [Q] − единица физической величины. Значение физической величины Q, найденное при измерении, называют действительным. В ряде случаев нет необходимости определять действительное значение физической величины, а достаточно определить принадлежность физической величины некоторой области Т: Контроль - это оценка соответствия физической величины установленному допуску. Средство измерений (СИ) - это техническое средство, используемое при измерениях и имеющее нормированные метрологические свойства. Для подтверждения этих свойств служит поверка. Поверка средств измерений – это совокупность операций, выполняемая органами государственной метрологической службы с целью подтверждения соответствия средств измерения установленным техническим требованиям. Существует огромное количество видов средств измерений, отличающихся по назначению, принципу действия, пределам измерений, точности. Поэтому в метрологии средства измерений классифицируются по определенным признакам. Средства измерения делятся на: эталоны; меры; образцовые средства; рабочие средства. Эталоны — средства измерений, официально утвержденные и обеспечивающие хранение и воспроизведение единицы физической величины с целью передачи ее размера другим средствам измерений. Меры — средства измерений, предназначенные для воспроизведения заданного размера физической величины. Образцовые средства измерения — применяются для поверки по ним других средств измерений. Это могут быть как меры, так и приборы и инструменты. Рабочие средства применяют для технических измерений, не связанных с передачей размера единиц Погрешность - отклонение результата измерения от истинного значения измеряемой величины. Точность измерений характеризуется близостью их результатов к истинному значению измеряемой величине. Истинное значение физической величины - это идеализация свойства объекта, не зависящее от средств познания и являющееся абсолютной истиной, к которой мы стремимся, пытаясь выразить в виде числа. Действительное значение физической величины - значение, найденное экспериментально, и настолько близкое к истинному, что может быть использовано вместо него. Принцип измерений - физическое явление или совокупность физических явлений, положенных в основу измерений. Метод измерений - совокупность приёмов использования принципов и средств измерений. Метод измерения должен по возможности иметь минимальную погрешность и способствовать исключению систематических погрешностей или переводу их в разряд случайных. |
