Однофазные электрические цепи переменного тока
Основные понятия и определения
Широкое применение в электрических цепях находят периодические ЭДС, напряжения и токи.
Периодические величины изменяются во времени по значению и направлению, причем эти изменения повторяются через некоторые промежутки времени Т, называемые периодом.
На практике подавляющее большинство промышленных источников переменного тока (генераторы электростанций) создают ЭДС, изменяющуюся по синусоидальному закону.
Преимущества такого закона:
а) простота получения;
б) напряжение легко трансформируется;
в) синусоидальная функция является единственной, которая в процессе интегрирования и дифференцирования не меняет своей формы и в процессе передачи и преобразования (в процессе трансформации) напряжения временная зависимость остается неизменной, т.е. синусоидальной.
Любая периодическая величина, изменяющаяся по синусоидальному закону, имеет ряд характерных параметров:
период - Т [c];
2) частота - f [Гц] .
Величина обратная периоду называется частотой:
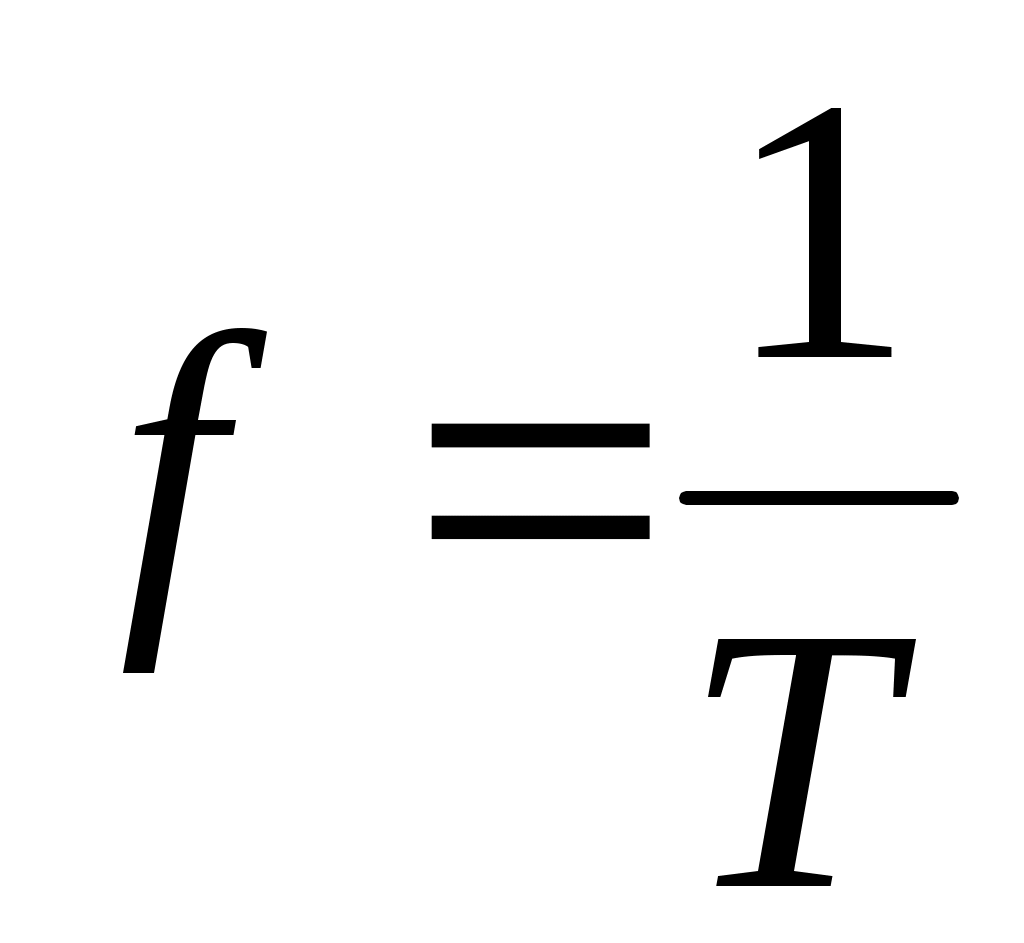 . .
Частота для всех электроустановок строго нормируется:
- для наземных систем - 50 (60)Гц;
- в авиации - 400Гц;
- космические летательные аппараты - 1000Гц.
Увеличение частоты позволяет уменьшить габариты электроустановок.
3) Циклическая частота - ω=2πf.
Для частоты 50Гц циклическая частота ω=2*3,14*50=314рад/с или 1/с.
4) Мгновенное значение- значение периодически изменяющейся величины в рассматриваемый момент времени.
Мгновенные значения обозначают - e, i, u.
5) Амплитудное значение
Максимальное значение или амплитуду ЭДС, напряжения и тока обозначают - Em, Um, Im.
6) Действующее значение
Действующее значение ЭДС, напряжения и тока обозначают - E, U, I.
Для количественной оценки синусоидального тока, который в течение времени непрерывно, периодически изменяется, используют значение постоянного тока, эквивалентное значению переменного тока по совершаемой работе. Такое значение будет действующимдля синусоидального тока.
Действующим (или эффективным)значением синусоидального тока называют такое значение постоянного тока, при протекании которого в одном и том же резисторе с сопротивлением Rза время одного периода Т выделятся столько же тепла, сколько при прохождении синусоидальнего тока.
При синусоидальном токе:
i=Imsinωt
количество теплоты, выделяемое в резисторе R за время Т равно:
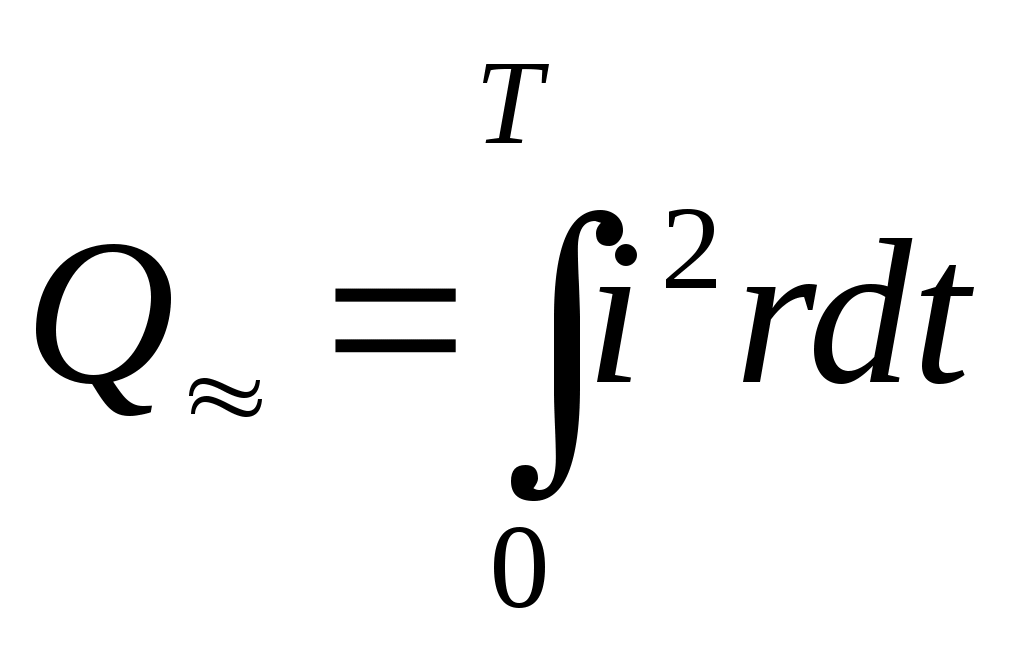 , ,
а при постоянном токе
 . .
Согласно определению Q≈=Q- , тогда
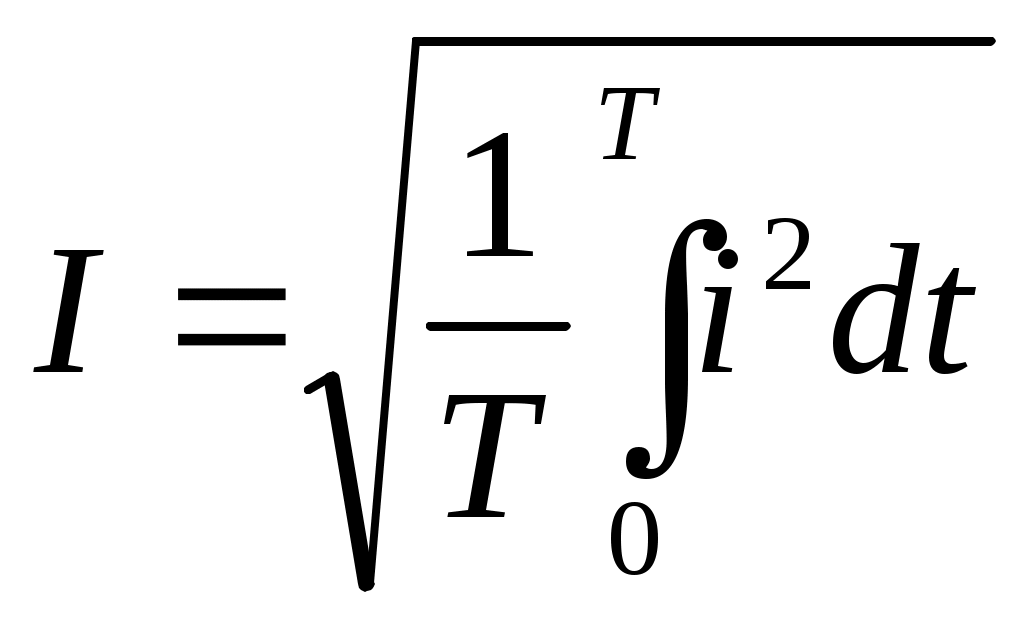 , , 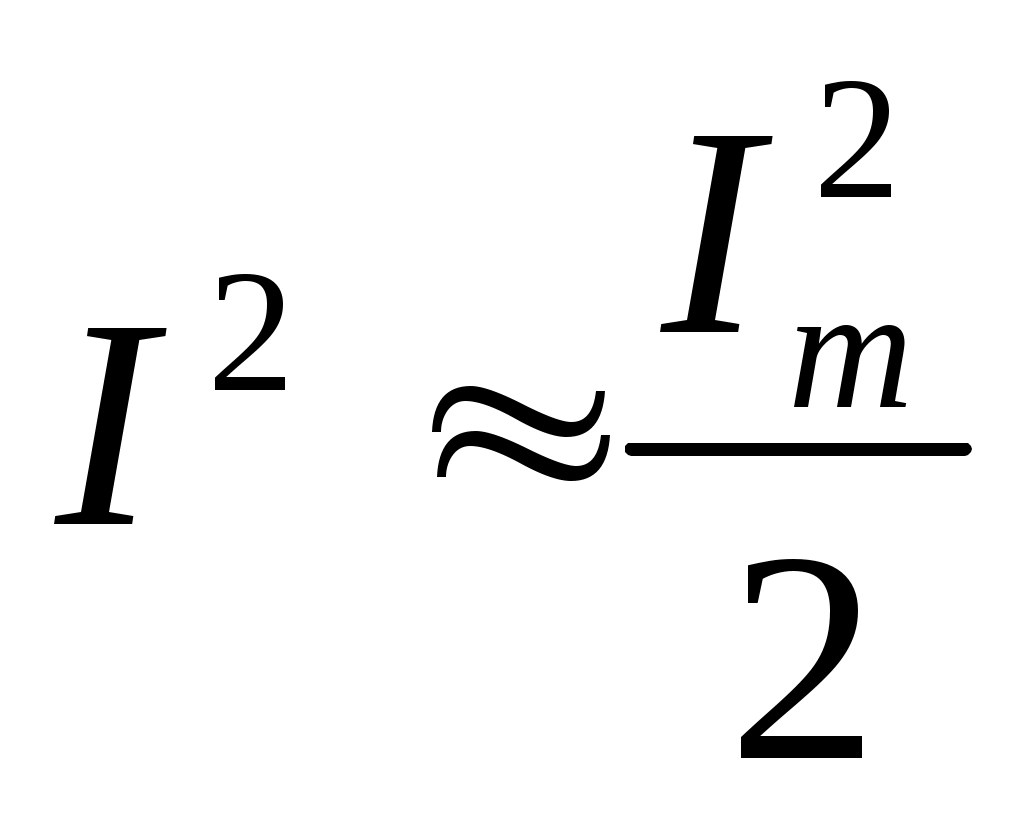 . .
Таким образом действующее значение синусоидального тока Iявляется его среднеквадратичным значением за период Т
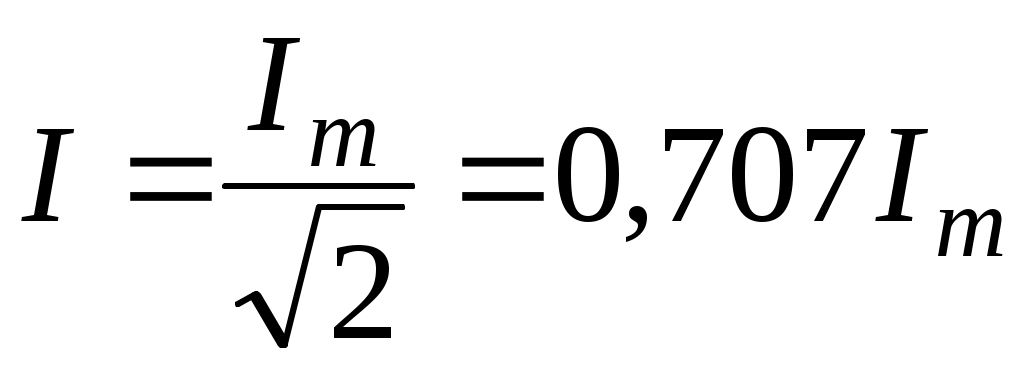
Действующее значение переменного тока обозначается как постоянный ток и в  раз меньше чем его амплитуда. раз меньше чем его амплитуда.
Аналогично

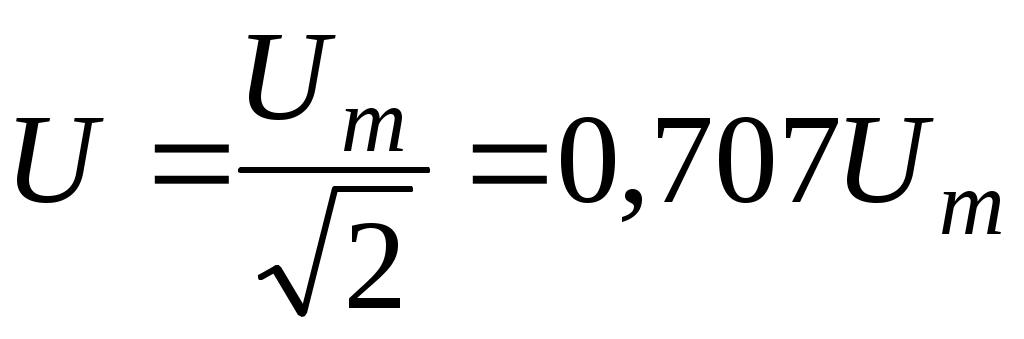 . .
Большинство электроизмерительных приборов работают на тепловом или электродинамическом эффекте, поэтому они всегда показывают действующее значение. Основные расчеты электроцепей синусоидального тока проводятся по действующим значениям. Для несинусоидальных величин эти соотношения будут другими.
7) Среднее значение
Среднее значение синусоидальной величины это ее среднеарифметическое значение. Однако, если определять среднее значение синусоидальной величины за период Т, то оно будет равно нулю, так как положительная и отрицательная полуволны синусоидальной кривой совпадают по форме. Поэтому среднее значение определяют за полпериода.
За среднее значение синусоидального тока принимают такое значение постоянного тока, при котором за полпериода переносится такой же электрический заряд, что и при синусоидальном токе:
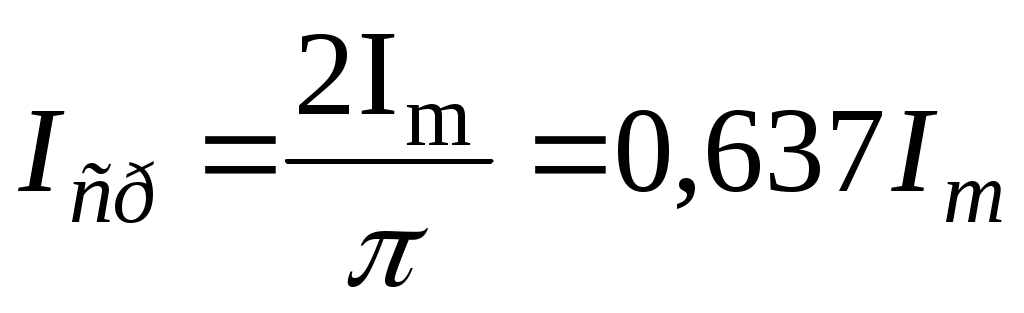 , ,
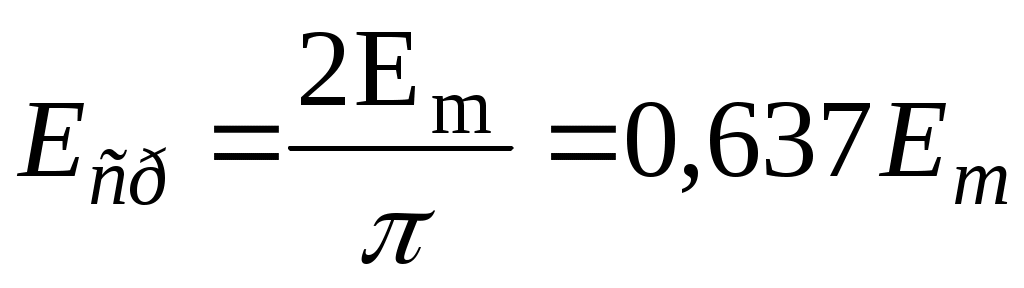 , ,
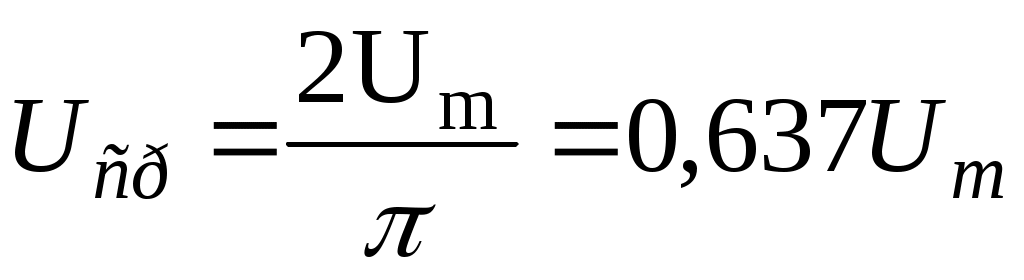 / /
Таким образом, среднее значение меньше действующего.
Изображение синусоидальных величин в прямоугольных координатах
В общем случае синусоидальные величины (рис.1), могут быть записаны:
e=Emsin(ωt+ψe)
u=Umsin(ωt+ψu),
i=Imsin(ωt+ψi),
где e,u,i - мгновенные значения ЭДС, напряжения и тока;
Em,Um,Im - амплитуды ЭДС, напряжения и тока.
(ωt+ψe) - фазовый угол;
ψe, ψu, ψi - начальные фазы ЭДС, тока и напряжения.
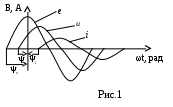
На практике чаще имеют место случаи, когда электрические величины не совпадают по фазе.
Из рис. 1 видно, что напряжение опережает ток на угол ψu-ψi . Разность фазовых углов называется разностью или сдвигом фаз.
φ=ψu-ψi - разность фаз между напряжением и током.
При этом пользуются правилом: начальные фазы расположенные по левую сторону от начала координат имеют положительные значения, а по правую отрицательные.
Если угол φ >0, то ток отстает от напряжения по фазе. Если φ<0, то ток опережает напряжение по фазе.
При сложении двух синусоидальных величин (одинаковой частоты), изображенных в прямоугольных координатах, необходимо сложить ординаты для ряда значений угла ωt и по точкам построить суммарную синусоиду. Получается новая амплитуда, новый фазовый сдвиг, причем:
Im≠Im1 + Im2;
φi≠ φi1+ φi2.
Такой расчет является трудоемким и имеет недостаточную точность.
В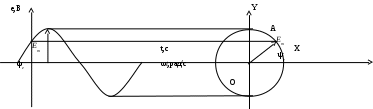 екторное изображение синусоидальных величин екторное изображение синусоидальных величин
Рис.2
Наиболее просто складывать синусоидальные величины, представив их вращающимися векторами (рис.3).
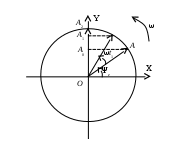
Рис.3
В плоскости с осями ОX и ОYрассмотрим вращающийся с постоянной скоростью, равной угловой частоте ω, вектор ОА, длина которого равна амплитуде синусоидальной ЭДС, т.е. 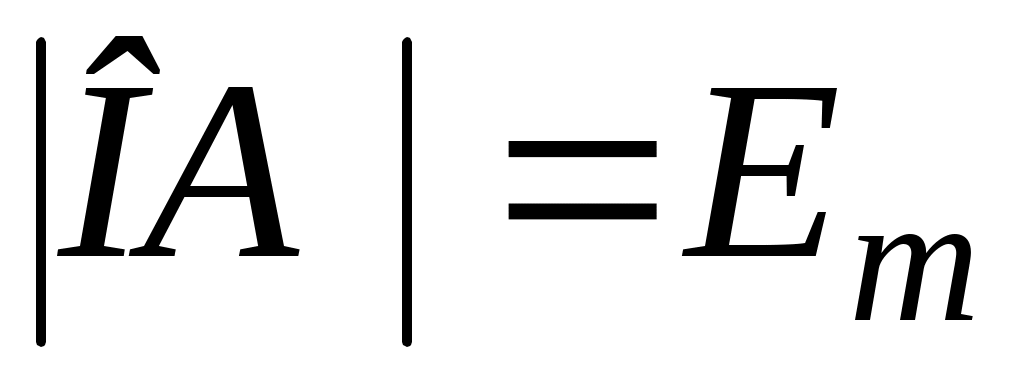 . .
Мгновенное значение ЭДС описывается известным соотношением:
e=Emsin(ωt+ψe).
За положительное направление вращения принимают направление против часовой стрелки, а угол поворота отсчитывают от оси ОX. В начальном положении (при t=0) вектор ОА повернут по отношению к оси OXна угол ψe
Построим проекцию вектора ОА на ось OY, которые изменяются по мере поворота вектора на угол ωt по отношению к начальному положению. В начальном положении (при t=0) проекция ОА0= Emsinψe=e0, т.е. равна мгновенному значению ЭДС при t=0.
Через некоторое время (t=t1) вектор ОА будет повернут на угол ωt1 и составлять с осью ОX угол (ωt1+ψe). Проекция его на ось OY:
ОА1= Emsin(ωt1+ψe)=e1, т.е. равна мгновенному значению ЭДС при t=t1.
При t=t2 вектор ОА совпадает с осью OY и его проекция ОА2=Em= e2. При дальнейшем вращении вектора АО его проекции на ось YO начнут уменьшаться, затем станут отрицательными и т.д.
Таким образом, проекции на ось OY вектора, вращающегося с постоянной скоростью ω и имеющего длину, равную амплитуде ЭДС, изменяются по синусоидальному закону, т.е. представляют собой мгновенные значения синусоидальной ЭДС. Следовательно, справедливо и обратное: если имеем синусоидальную величину. то ее можно представить вращающимся вектором.
Правила построения векторных диаграмм
Любую синусоидально изменяющуюся во времени величину (ЭДС, напряжение, ток) можно представить в виде вращающегося вектора, длина которого равна амплитуде, а угловая скорость угловой частоте этой синусоидальной величины.
Начальное положение вращающегося вектора определяется углом, равным начальной фазе синусоидальной величины и откладываем от положительного направления оси O в сторону, противоположную вращению часовой стрелки.
В одних и тех же осях можно представить векторы всех ЭДС, действующих в данной цепи, напряжений на всех участках данной цепи и токов во всех ее ветвях (в заданных масштабах).
Так как синусоидальные величины имеют одинаковую частоту, то изображающие их векторы вращаются с одинаковой скоростью. Их взаимное положение на плоскости, относительно друг друга, остается неизменным. Поэтому на практике векторы не вращают, а строят их, соблюдая углы между векторами (углы сдвига фаз).
Отказавшись от вращения вектора можно строить векторы не только максимальных, но и действующих значений.
Вектора можно складывать, по правилу параллелограмма, получив при этом суммарный вектор (рис. 4).
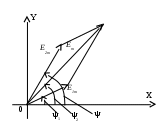
Рис.4
В связи с отсутствием необходимости вращения нас интересует только взаимное расположение векторов, один из которых можно строить по направления оси OX, остальные вектора направляются относительно этого вектора (рис.5).
Например, если к элементам электрической цепи подается переменное напряжение u=Umsin(ωt+ψu), то возникнет переменный ток i=Imsin(ωt-ψi). В этом случае ток отстает от напряжения по фазе на угол φ=ψu-ψi. Начальные фазы ψu и ψi на векторной диаграмме не изображают, так как взаимное положение векторов определяется полностью разностью фаз - φ. Принимаем начальную фазу тока равную нолю (ψi=0), тогда начальная фаза напряжения ψu равна сдвигу фаз - φ.
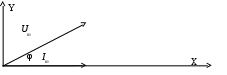
Рис.5
Графический метод расчета является грубым неточным. На практике переходят к точным математическим методам расчета на основе теории комплексных чисел.
Понятия о комплексных числах
Комплексная плоскость - прямоугольная системе координат, на которой по одной оси откладываются вещественные числа +1, на другой (перпедикулярной) - мнимые числа +j.
Здесь j= - мнимая единица. - мнимая единица.
Действия с мнимой единицей:
1)j2=-1; 2) 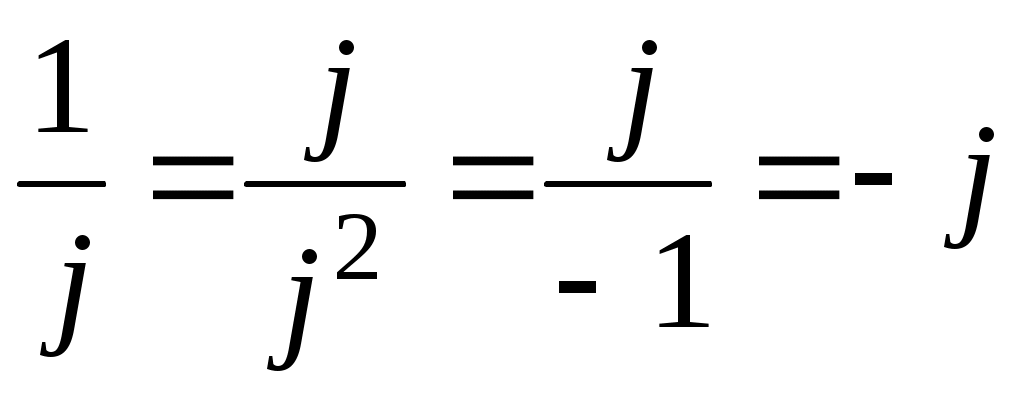
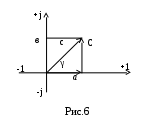
Любую точку на комплексной плоскости можно охарактеризовать комплексным числом. Известно, что комплексное число С имеет вещественную Re и мнимую Im составляющие.
Алгебраическая форма записи комплексного числа:
С=а+jв,
где а= Аcosα– реальная часть комплексного числа,
в= Аsinα– мнимая часть, γ=arctg - фаза, - фаза,
с=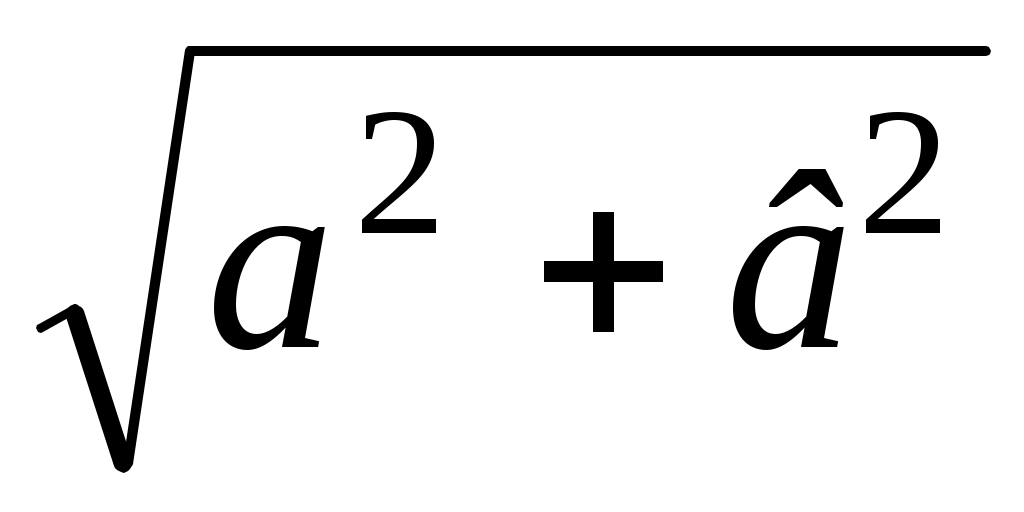 - модуль комплексного числа. - модуль комплексного числа.
Тригонометрическая форма записи комплексного числа:
С=с(cosγ+jsinγ).
Показательная форма записи комплексного числа:
 , где , где  - оператор поворота (поворотный множитель). - оператор поворота (поворотный множитель).
cosγ + jsinγ =  - формула Эйлера. - формула Эйлера.
Частные случаи:
Для γ= π/2 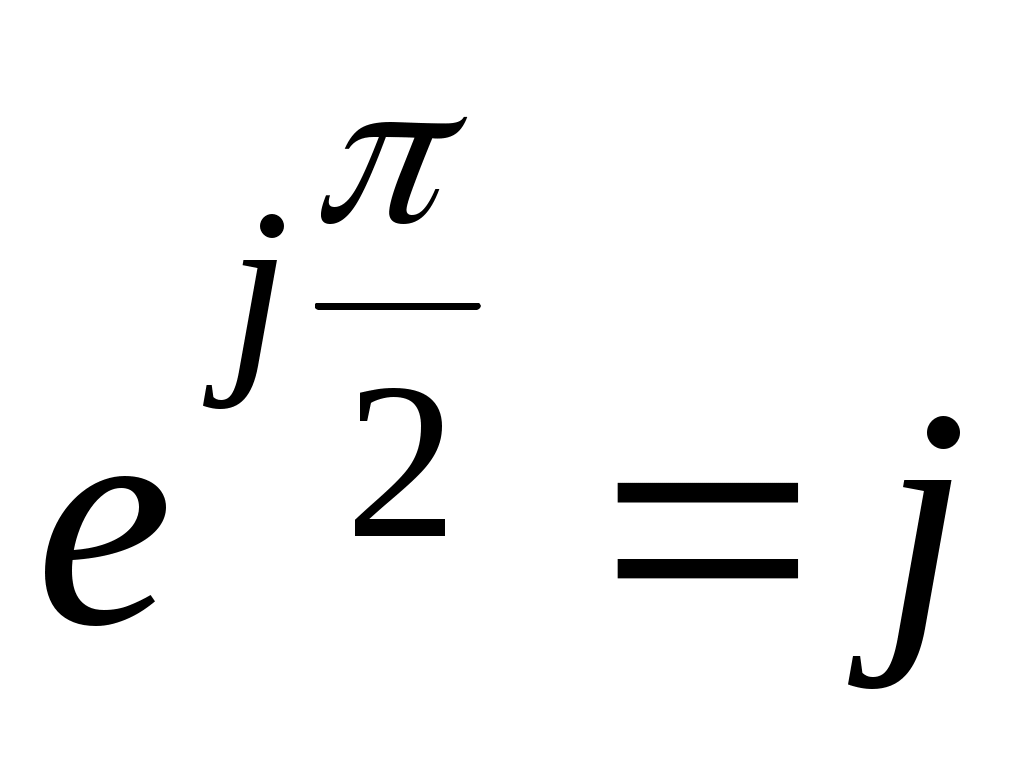 ; ;
γ= -π/2 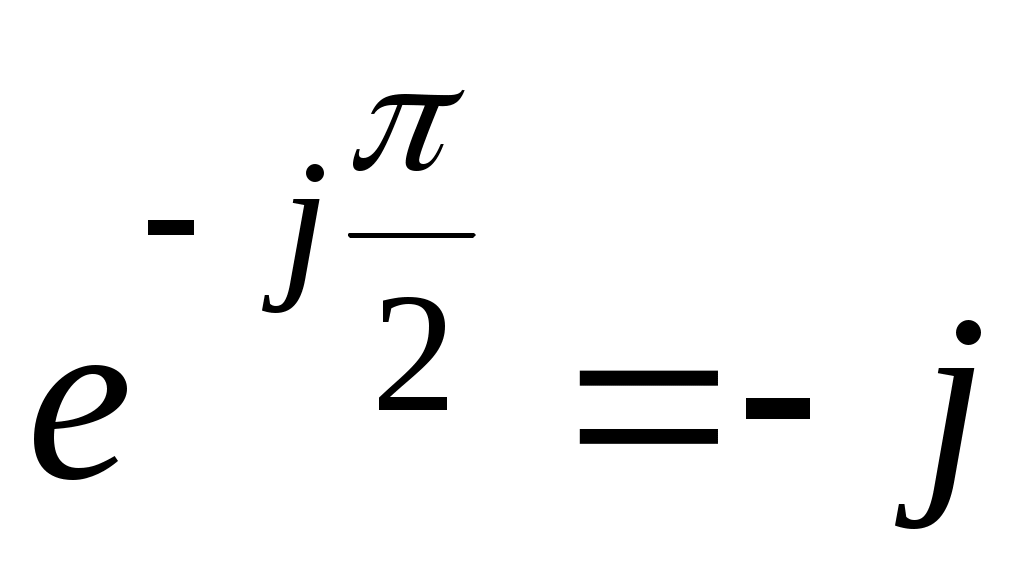 ; ;
γ= π 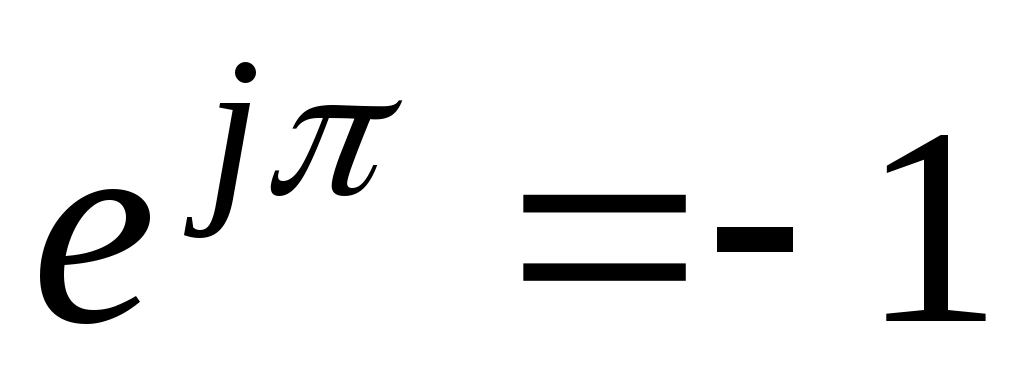 . .
Тригонометрическая форма записи служит для перехода из алгебраической формы в показательную и наоборот.
Изображение синусоидальных величин с помощью комплексных чисел
Синусоидальный ток i=Imsin(ωt+ψi) может быть изображен на комплексной плоскости (рис.7). Величина и направление вектора Im определяются координатами одной точки комплексной плоскости Im и этот вектор записывается с помощью комплексного числа:
 , ,
 - вектор вращается со скоростью ω против часовой стрелки; - вектор вращается со скоростью ω против часовой стрелки;
 - положение вектора при t=0 (начальное положение). - положение вектора при t=0 (начальное положение).
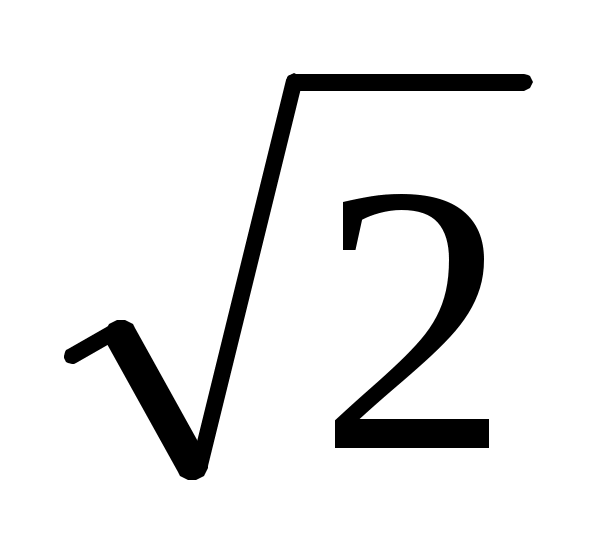 и и  можно опустить как постоянные составляющие, тогда получаем комплексное действующее число (комплекс тока) в показательной форме: можно опустить как постоянные составляющие, тогда получаем комплексное действующее число (комплекс тока) в показательной форме:
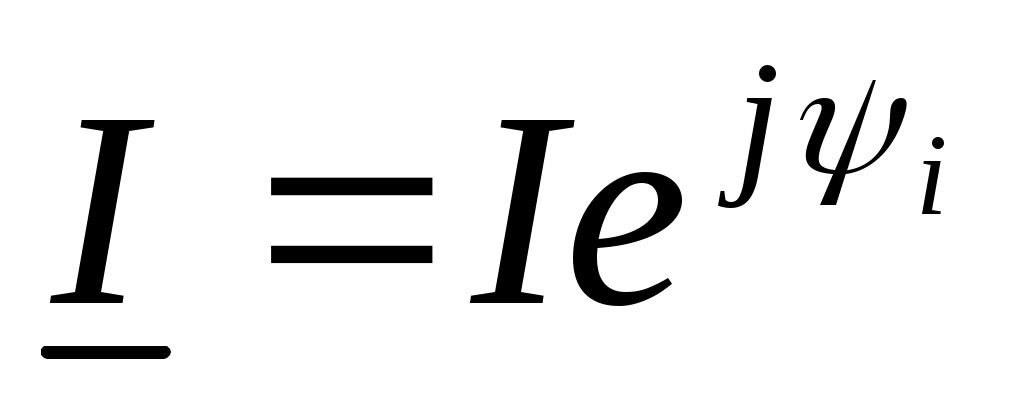


+j

 

Im
Im(Im)
+1
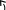
Ψi

O
Рис.7
Закон Ома в комплексной форме

Рис.8
Если на элементе электрической цепи присутствует напряжение u=Umsin(ωt+ψu) и ток через него i=Imsin(ωt+ψi), тогда
U=Uej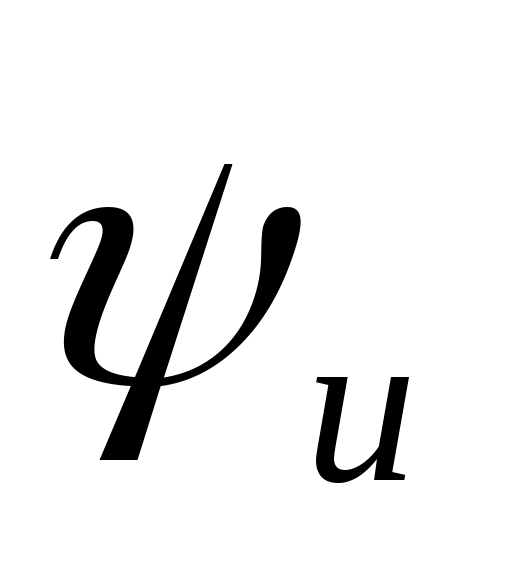
I=Iej
φ=ψu-ψi
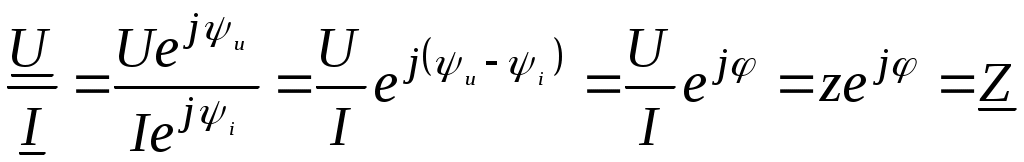
Здесь
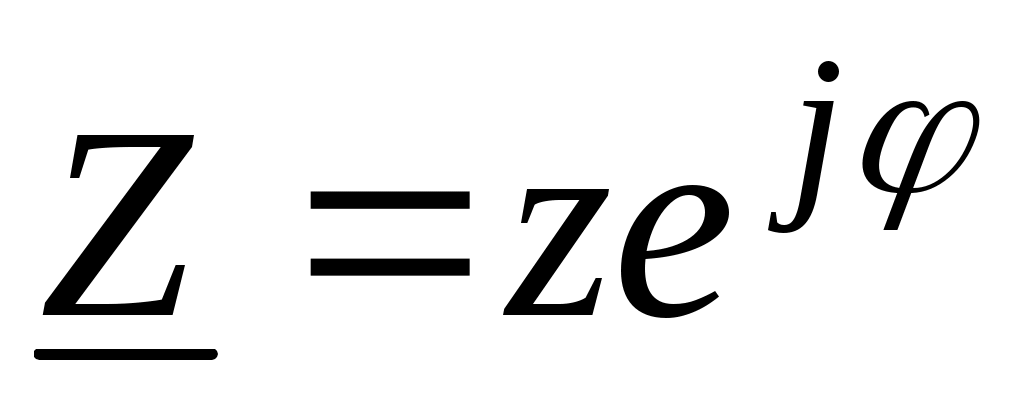 - полное комплексное сопротивление цепи переменного тока в показательной форме записи; - полное комплексное сопротивление цепи переменного тока в показательной форме записи;
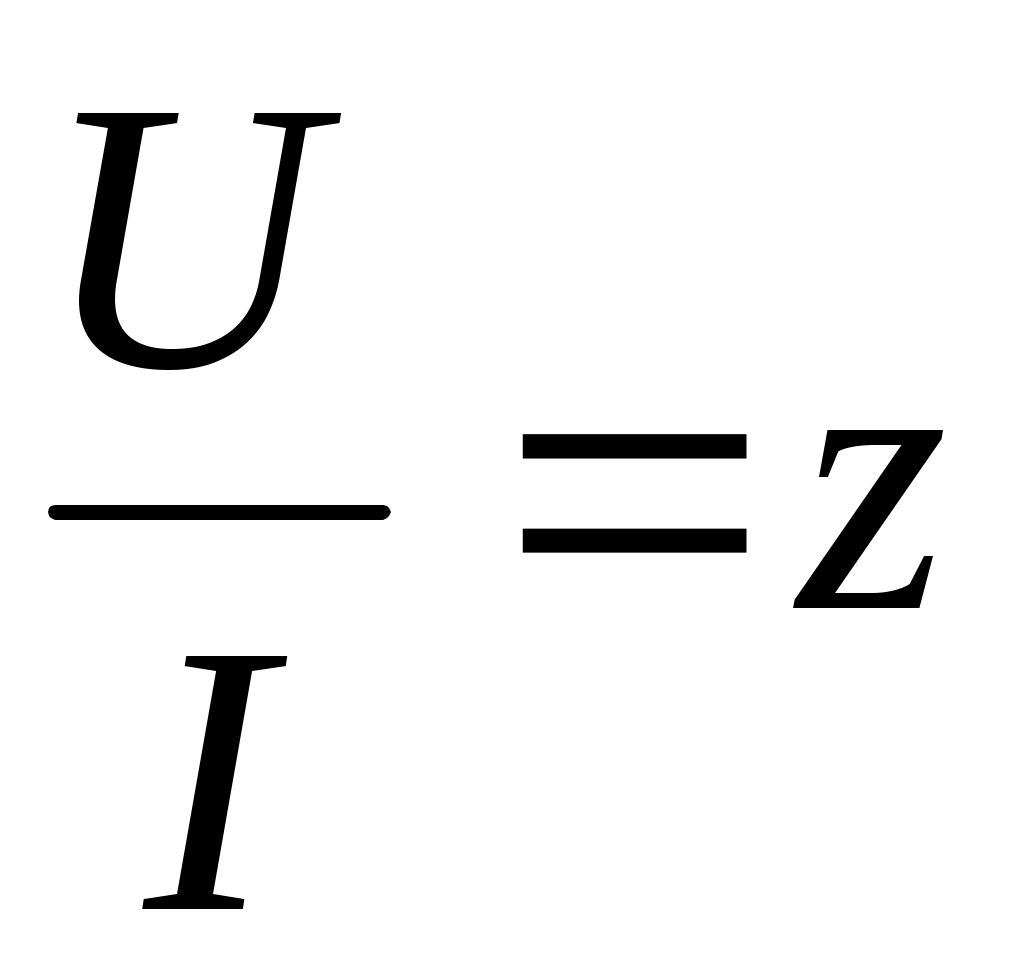 - модуль полного сопротивления; - модуль полного сопротивления;
φ - разность фаз между напряжением и током.
Z=z(cosφ + jsinφ) = R + jX- алгебраическая форма записи полного сопротивления.
R – вещественная часть комплексного числа, активное сопротивление;
Х – мнимая часть комплексного числа, реактивное сопротивление.
Проводимость цепи:
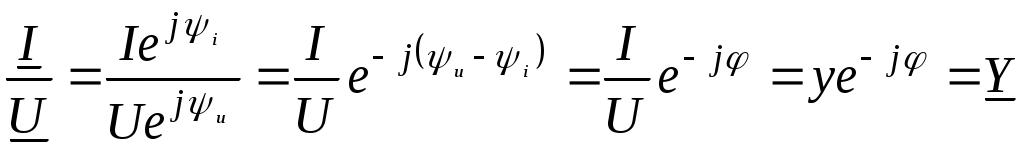
 - полная комплексная проводимость цепи переменного тока в показательной форме записи; - полная комплексная проводимость цепи переменного тока в показательной форме записи;
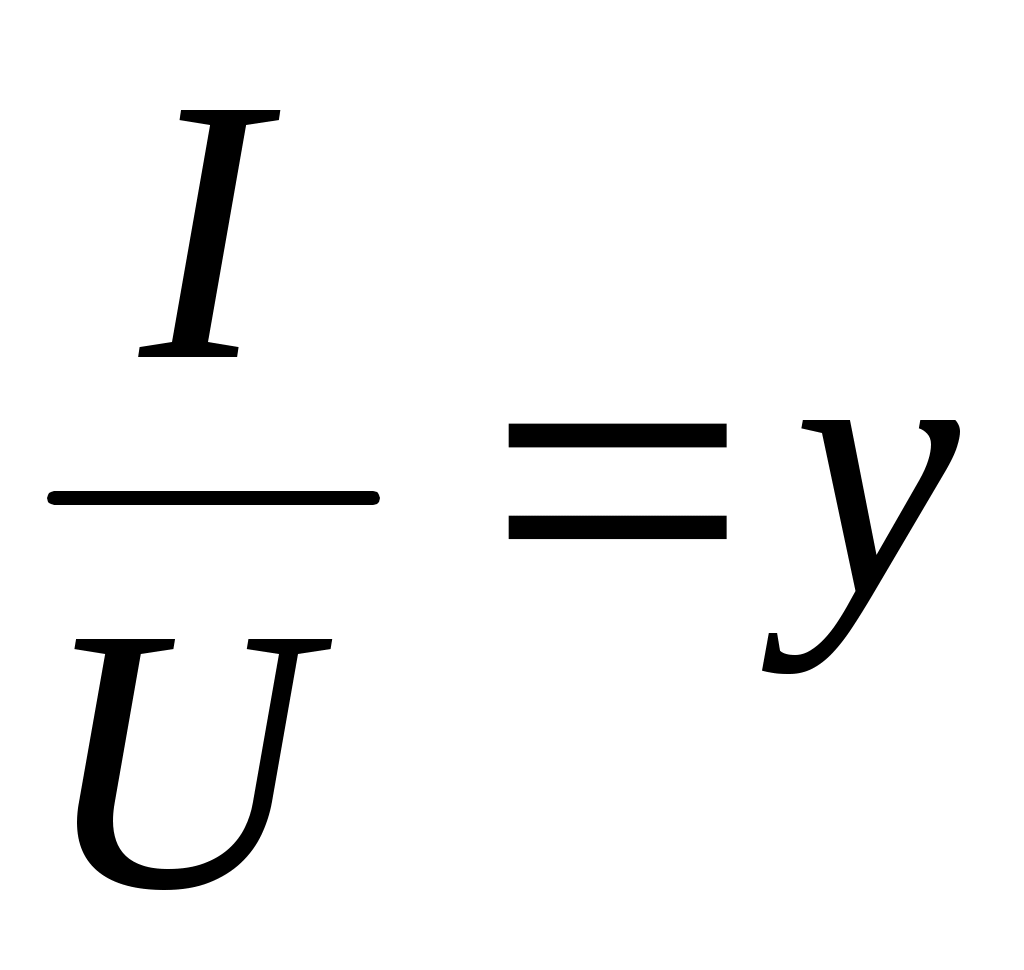 - модуль полной проводимости; - модуль полной проводимости;
Y=y[cos(-φ) + jsin(-φ)] = ycosφ - jysinφ = G + jB- алгебраическая форма записи полной проводимости.
G – вещественная часть, активная проводимость;
B – мнимая часть, реактивная проводимость.
Законы Кирхгофа для электрической цепи синусоидального тока
Для электрической цепи синусоидального тока так же справедливы законы Кирхгофа, сформулированные ранее для цепи постоянного тока. Но так как синусоидальные величины характеризуются мгновенными, амплитудными и действующими значениями, то для каждого из них существуют свои формулировки законов Кирхгофа.
Для мгновенных значений законы Кирхгофа справедливы в алгебраической форме.
Первый закон: Алгебраическая сумма токов, сходящихся в узле равна нулю:
 , ,
где n - число ветвей, сходящихся в узле;
Второй закон - алгебраическая сумма ЭДС в замкнутом контуре равна алгебраической сумме падений напряжений на сопротивлениях этого контура:  , ,
где m - число ЭДС в контуре, а n - число ветвей или число сопротивлений в контуре.
Для амплитудных и действующих значений закон Кирхгофа справедлив только в комплексной форме.
Первый закон: Сумма комплексных токов в узле равна нулю:
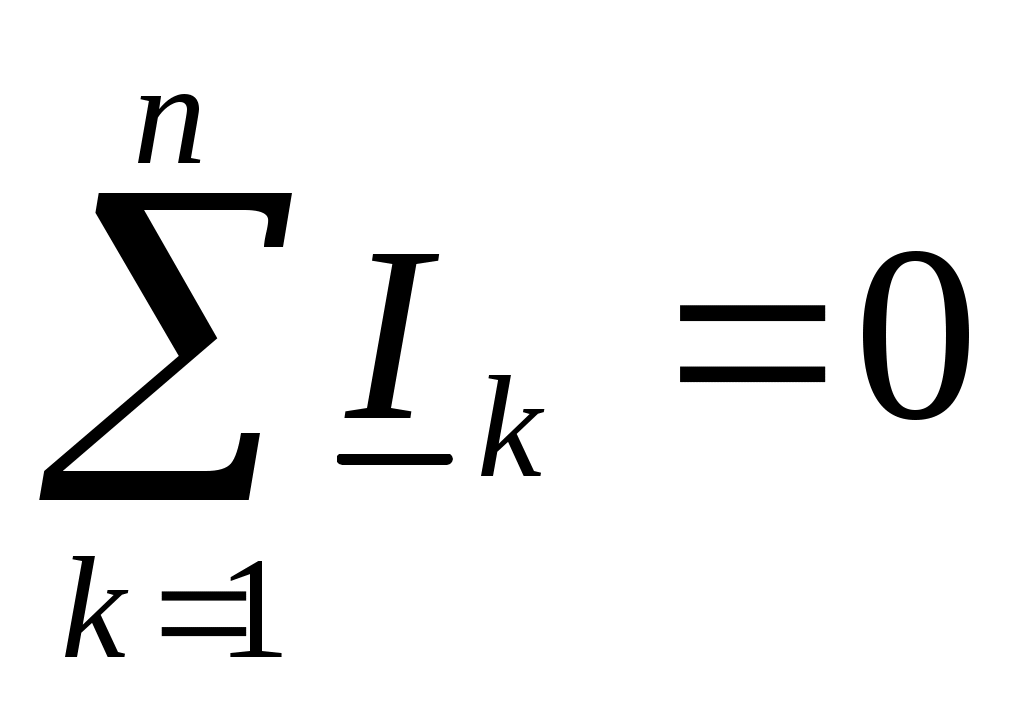
Второй закон: сумма комплексных ЭДС в контуре равна сумме комплексных падений напряжений на сопротивлениях этого контура:
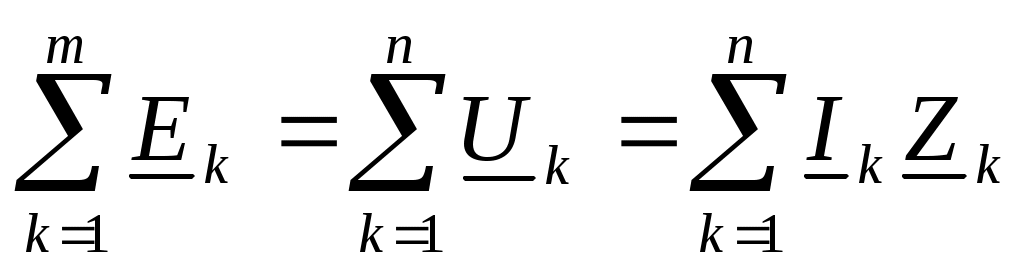
Электрическая цепь с активным сопротивлением
Электрический ток в металлах представляет собой направленное движение электронов. При движение электроны сталкиваются с атомами проводящего вещества и кинетическая энергия, запасенная ими при ускорении, превращается в тепловую. Проводник нагревается и тепло рассеивается в окружающую среду. Это необратимый активный процесс преобразования энергий, который количественно определяется сопротивлением R. Поэтому его называют активным сопротивлением.
В цепях постоянного тока сопротивление R называют просто сопротивлением. В цепях синусоидального тока называют активным сопротивлением.
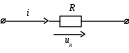
Рис.9
В цепи переменного тока с активным сопротивлением (рис.9) действуют:
ток i=Imsin(ωt+ψi), напряжение на активном сопротивлениеuR=Ri=RImsin(ωt+ψi)=Umsin(ωt+ψi),
Um=RIm
Действующие значения тока и напряжения в комплексной форме:
UR=UR ej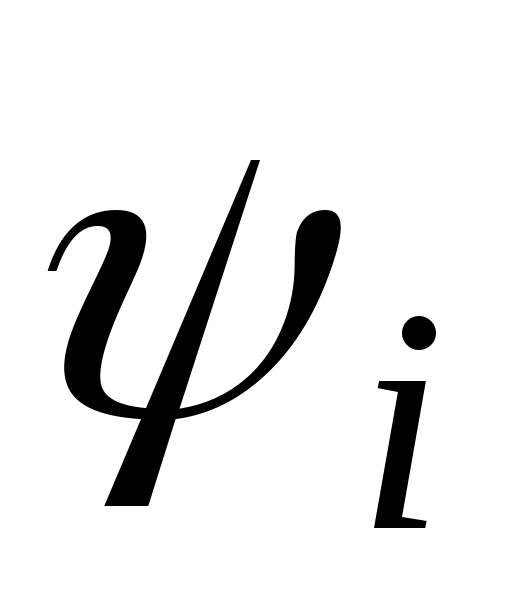
I=Iej
Полное сопротивление:
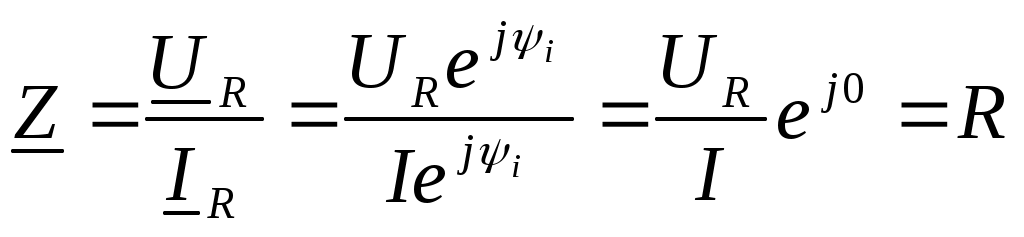
Сопротивление R – положительное вещественное число.
Ток в элементе с активным сопротивлением совпадает по фазе с напряжением на этом элементе (рис.10). На векторной диаграмме ток и напряжение совпадают по направлению(рис.11).

Рис.11
Электрическая цепь с индуктивностью
Индуктивностью L теоретически обладают все проводники с током. Но в некоторых случаях эта индуктивность пренебрежимо мала. Значительна индуктивность у обмоток или катушек, состоящих из большого числа витков провода. Индуктивность возрастает, если созданный током магнитный поток Ф замыкается по пути с малым магнитным сопротивлением (например по стальному сердечнику), в следствие чего магнитный поток увеличивается. Индуктивностью обмоток нельзя пренебрегать при рассмотрении физических процессов в электродвигателях, трансформаторах, дросселях. L- коэффициент пропорциональности между потокосцеплением и током, постоянная величина для каждого проводника.
Размерность индуктивности L - (Гн, генри).
Реальная катушка кроме индуктивности обладают значительным активным (омическим) сопротивлением Rи емкостным сопротивлением с емкостью С. Для сечение S, длины l и материала (коэф. удельного сопротивления материала ρ) обмоточного провода:
R=ρl/S.
В простейшем случае рассматривают идеальную катушку с постоянной индуктивностью L= const, сопротивлением R=0, емкость витков простейшем случае рассматривают идеальную катушку с постоянной индуктивностью L= const, сопротивлением R=0, емкость витков
Пусть к цепи с индуктивностью L (рис.12) приложено синусоидальное напряжение u=Umsinωt. Под действием этого напряжения в цепи создается синусоидальный токi. Этот ток создает магнитный поток Ф, который согласно закону электромагнитной индукции индуцирует в катушке ЭДС самоиндукции: Рис.12
eL=-dψ/dt=-WdФ/dt=-Ldi/dt,
где ψ - потокосцепление ψ=Li=WФ,
W - число витков, Ф - магнитный поток.
Знак минус согласно принципу электромагнитной индукции Ленца указывает на то, что ЭДС самоиндукции eL всегда имеет такое направление, при котором она препятствует изменению магнитного потока и тока в цепи.
Выбираем условные положительные направления тока, напряжения и ЭДС, причем условное положительное направление ЭДС в любой момент времени противоположно падению напряжения на катушке:
eL=-uL.
По второму закону Кирхгофа:
u=-eL, u =uL
или
Umsinωt=Ldi/dt
Получаем дифференциальное уравнение
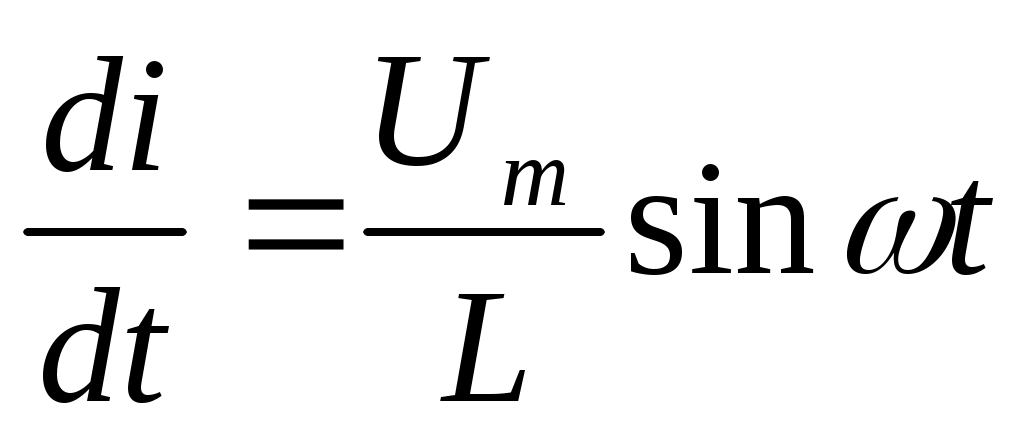
Решая это уравнение получим выражение для тока в цепи:
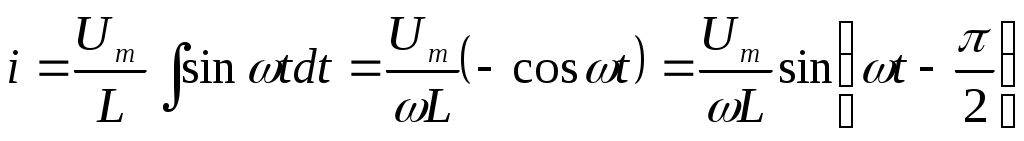
Или i=Imsin(ωt-π/2), где Im=Um/ωL
Таким образом ток в цепи с индуктивностью изменяется по синусоидальному закону и отстает от напряжения на угол π/2 (рис.13).
Знаменатель ωL имеет размерность сопротивления – это индуктивное сопротивление xL.
xL= ωL=2πfL.
Следовательно получаем:
Im=Um/xL –для амплитудного значения тока;
I=U/xL –для действующего значения тока.
В комплексной форме:
U=Uej0 = U ,
I=Ie-jπ/2=-jI .
Индуктивное сопротивление в комплексной форме
  – положительное мнимое число. – положительное мнимое число.
Н а векторной диаграмме вектор напряжения опережает вектор тока на угол π/2 (рис.14). а векторной диаграмме вектор напряжения опережает вектор тока на угол π/2 (рис.14).
Рис.14
Электрическая цепь с емкостью
Элементом электрической цепи, обладающей значительной емкостью, является конденсатор. Конструктивно конденсатор представляет собой две пластины с большой (по сравнению с зазором между пластинами) поверхностью, разделенные между собой диэлектриком. Емкость С конденсатора определяет тот электрический заряд, который накапливается на пластинах при разности потенциала между ними в 1В. Размерность емкости С – (Ф, фарад).
1мкФ=10-6Ф (микрофарада)
1пФ=10-12Ф (пикафарада)
1нФ=10-9Ф (нанафарада).
Зазор в конденсаторе не является препятствием для прохождения переменного тока, так как синусоидальное напряжение периодически меняется по направлению, следовательно, так же непрерывно меняется заряд на обкладках конденсатора (конденсатор перезаряжается).
Реально емкостью обладают любые два проводника, расположенные недалеко друг от друга, но при малой поверхности (по сравнению с зазором) их емкость не велика и ею пренебрегают.
В простейшем случае рассматривают идеальный конденсатор с емкостью С=const, его сопротивление R=0, индуктивность L=0. простейшем случае рассматривают идеальный конденсатор с емкостью С=const, его сопротивление R=0, индуктивность L=0.
Пусть к цепи с конденсатором, емкость которого С, приложено синусоидальное напряжение u=Umsinωt. Под действием этого напряжения в цепи создается синусоидальный ток i и на каждой пластине скапливается заряд Q=Cuc, где uc – падение напряжения на конденсаторе.
Рис.15
Выбираем условные положительные направления тока, напряжения и ЭДС. По второму закону Кирхгофа u=uc, тогда заряд на конденсаторе Q=Cuc=СUmsinωt.
Ток в цепи представляет собой изменение заряда во времени:
i=dQ/dt=ωCUmcosωt=ωCUmsin(ωt+π/2), i=Imsin(ωt+π/2), Im=Um/(1/ωC).
Таким образом, ток в цепи с конденсатором так же изменяется по синусоидальному закону и опережает напряжение на угол π/2 (рис.16).
Знаменатель 1/ωCимеет размерность сопротивления – это емкостное сопротивление хс:
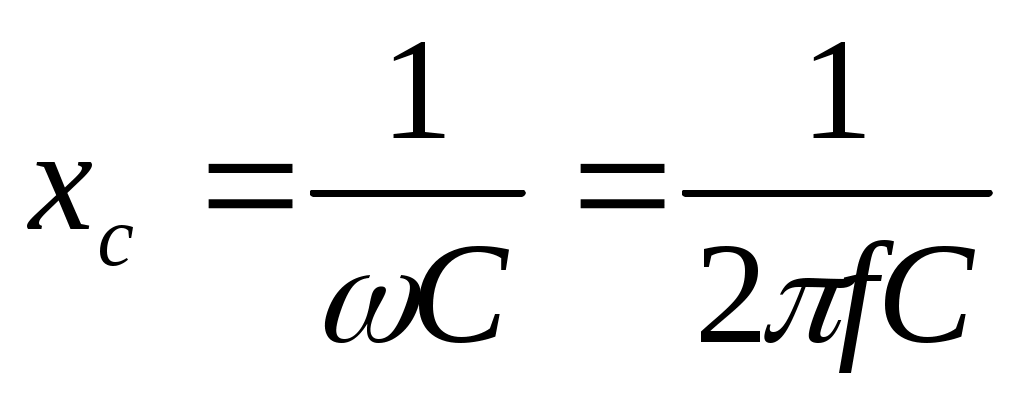 . .
Следовательно получаем
Im=Um/xс –для амплитудного значение тока;
I=U/xс –для действующего значения тока.
В комплексной форме:
U=Uej0 = U ,
I=Iejπ/2=jI .
Индуктивное сопротивление в комплексной форме
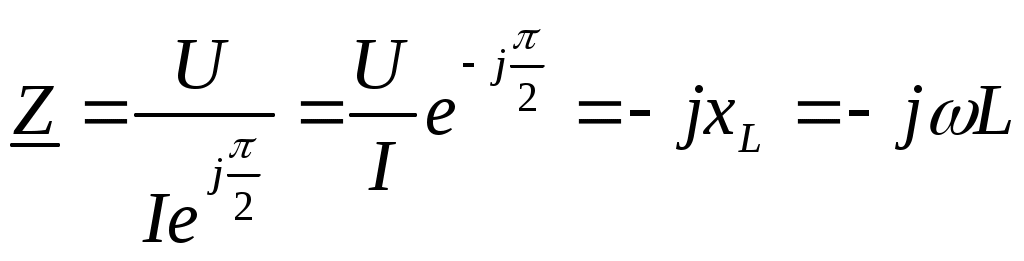 – отрицательное мнимое число. – отрицательное мнимое число.
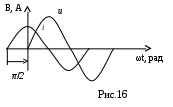
На векторной диаграмме вектор напряжения отстает от вектора тока на угол π/2 (рис.17).
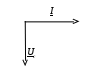
Рис.17
Электрическая цепь при последовательном соединение r, L и С элементов
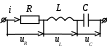
Рис.18
К электроцепи ( рис.18) подводится напряжение u, под действием которого по цепи течет ток i = Imsinωt.
По второму закону Кирхгофа запишется уравнение:
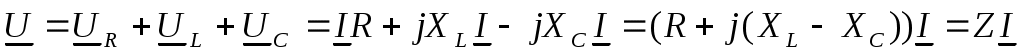 , ,
где 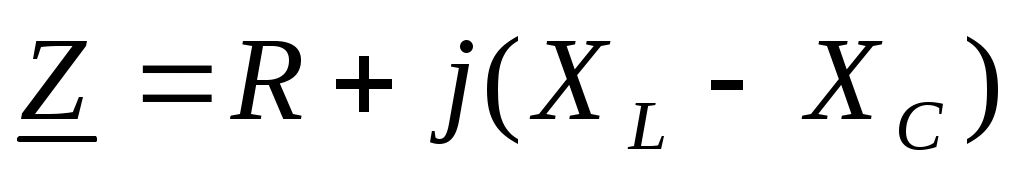 ; ; 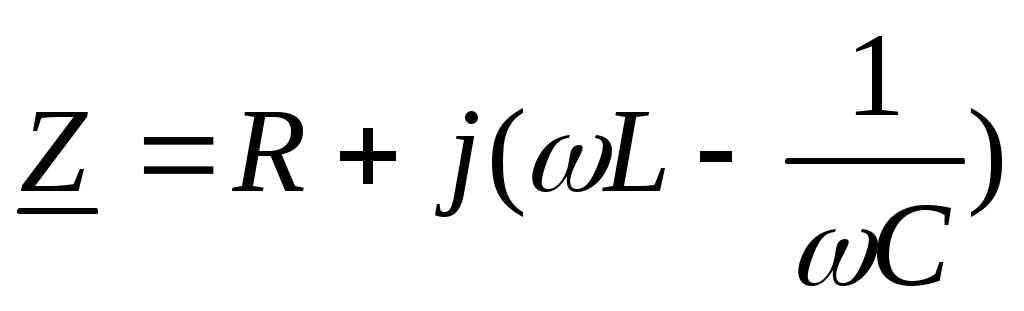 . .
В показательной форме 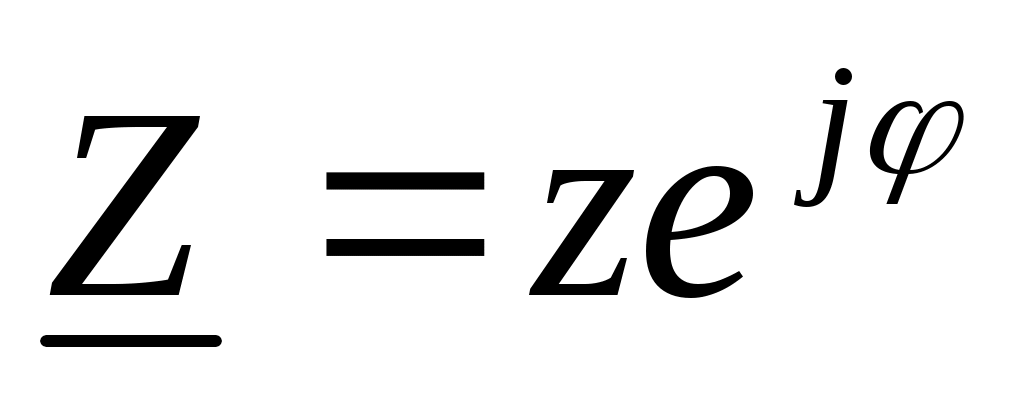 , ,
где 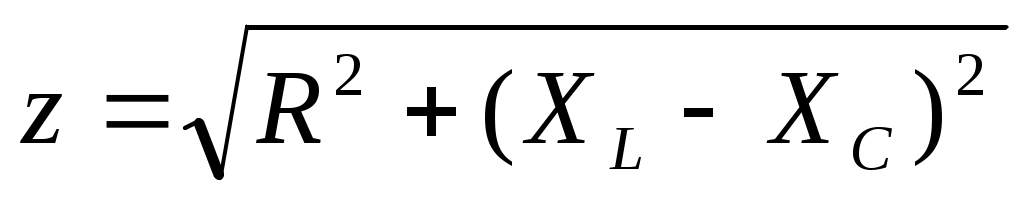 и и 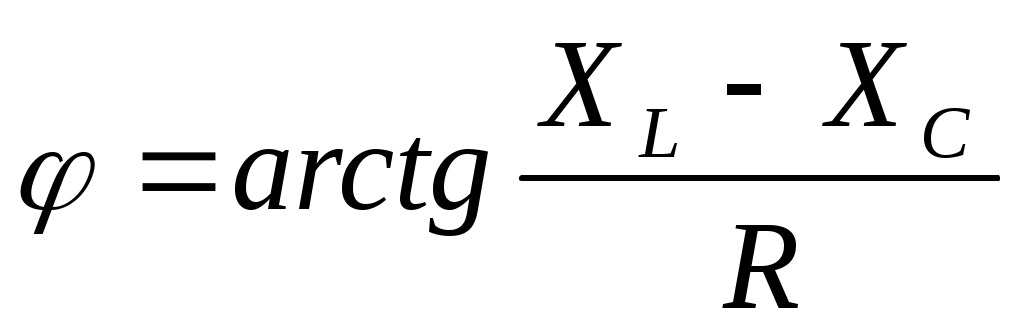 определяются из треугольника сопротивлений (рис.19). определяются из треугольника сопротивлений (рис.19).

Рис.19
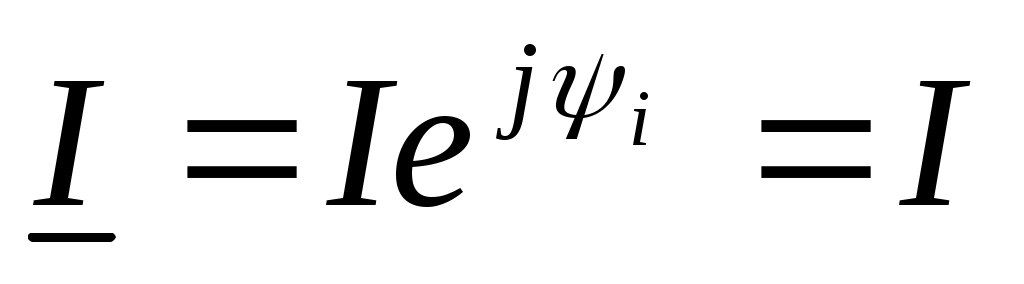 , так как ψi =0. , так как ψi =0.
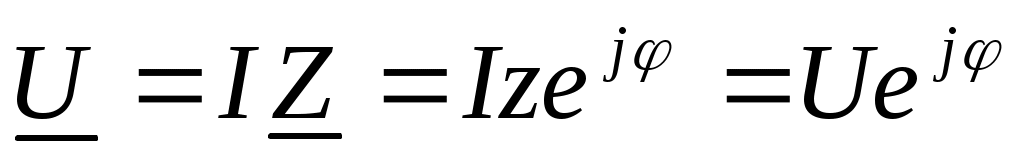 , U=zI , U=zI
Мгновенное значение напряжения u=Umsin(ωt+φ).
Вывод: напряжение опережает ток на фазный угол φ.
В зависимости от соотношения сопротивлений ХLиXC цепь имеет характер:
а) индуктивный, если ХL> XC, при этом φ>0;
б) емкостный, если ХL< XC,при этом φ<0
в) резонанс, если ХL= XC, при этом φ=0.
На рис. 20 приведены векторные диаграммы напряжений и синусоиды напряжений и токов, соответствующие трем выше изложенным режимам.
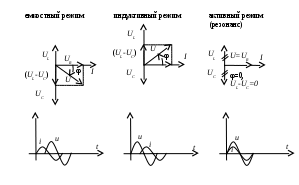
Рис.20
Резонансные явления
Под резонансом понимают явление резкого возрастания амплитуды колебания, когда частота внешнего возмущения и силы совпадает с частотой собственных колебаний системы.
Имеем цепь, которая кроме активного сопротивления содержит и реактивные составляющие. Несмотря на это цепь, имеет активный характер, то есть ток и напряжение совпадают по фазе. Тогда в этой цепи наблюдается резонанс.
Условия резонанса:
i=Imsinωt, u=Umsin(ωt+φ), I=I, U=Uejφ, Z=Zejφ=R+j(xL-xC)=R+jx.
При резонансе: xL=xC, ωL=1/ωC, xL-xC=0, x=0, φ=0
При резонансе полное комплексное сопротивление является вещественным числом Z=R.
Для проводимости:Y=Ye-jφ=g-j(bL-bC)=g-jb, где bL=bC, b=0, φ=0, Y=g.
Резонанс напряжений.
Резонанс напряжений возможен в цепях с последовательно соединенными катушкой индуктивности и конденсатором.
Если xL=xC, то есть ω0L=1/ω0C, где ω0 – резонансная частота или собственная частота цепи.
 , , 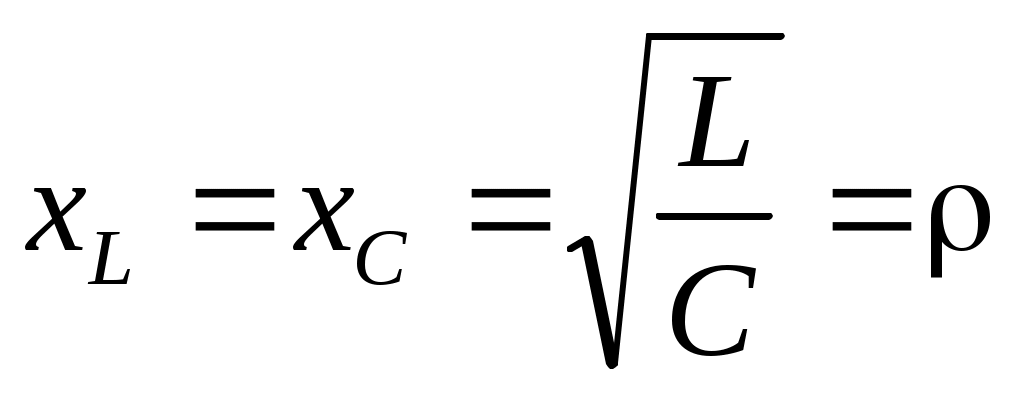 - волновое сопротивление. - волновое сопротивление.
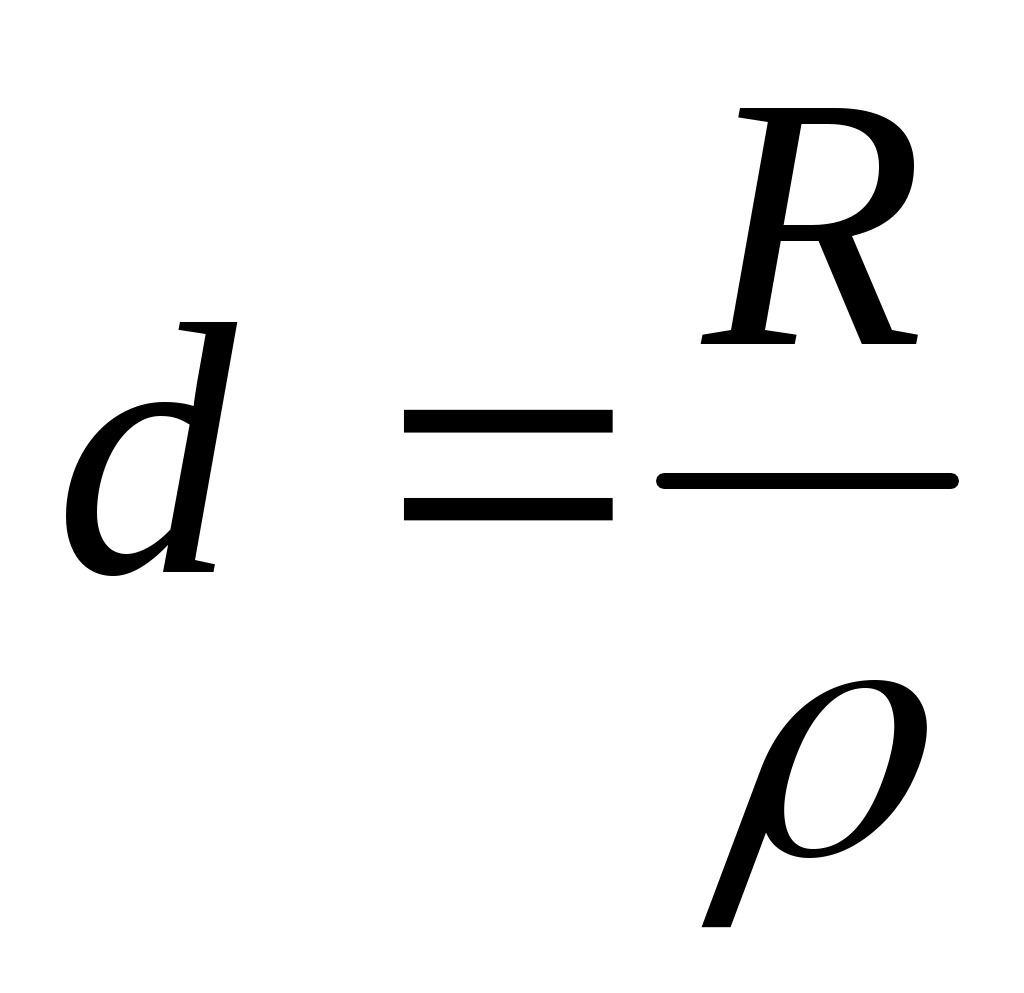 - характеризует насколько резко выражено явление резонанса в цепи. - характеризует насколько резко выражено явление резонанса в цепи.
 - добротность определяет во сколько раз напряжение на каждом реактивном из реактивных элементов больше, чем подведенное к цепи напряжение. - добротность определяет во сколько раз напряжение на каждом реактивном из реактивных элементов больше, чем подведенное к цепи напряжение.
Q – определяет качество конура.
Q=200-500 для радиотехнических контуров.
Так как сопротивление и напряжение находятся в прямо пропорциональной зависимости, то UL=UC, отсюда название – резонанс напряжений. Напряжение на конденсаторе и катушке индуктивности взаимно компенсируют друг друга при резонансе, причем эти два напряжения при резонансе больше чем напряжение источника.
Для действующих значений:
UL=xLI, UC=xCI, UR=RI
При резонансе
UL=ρI, UC=ρI, U= rI,
 , если ρ ›› R, то ULи UC›› U , если ρ ›› R, то ULи UC›› U
Добротность Qопределяет качество контура. Для радиотехнических контуров Q=200500. Добротность Qопределяет во сколько раз напряжение на каждом реактивном элементе больше чем напряжение, подведенное к цепи.
Ток при резонансе имеет максимальное значение. Так как сопротивление цепи определяется только активной составляющее, следовательно, минимально, а как известно сопротивление и ток находятся в обратно пропорциональной зависимости.
I=U/R
При резонансе происходит взаимный обмен энергией между катушкой и конденсатором. Поэтому реактивная составляющая мощности равна нулю. Коэффициент мощности при резонансе имеет максимальное значение.
Резонанс токов.
|
 Скачать 436 Kb.
Скачать 436 Kb.