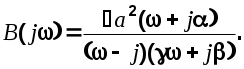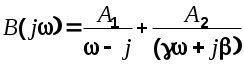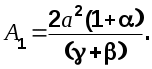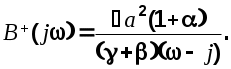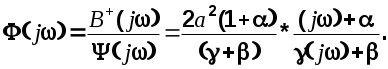|
|
07_Линейные непрерывные САУ при случайных воздействиях. Оглавление Случайные функции и их характеристики
Оглавление 6.1. Случайные функции и их характеристики………….1 6.2. Связь между корреляционными функциями и спектральными плотностями на входе и выходе линейной динамической системы……………………4 6.3. Анализ динамической точности САУ……………… 6 6.4. Формирование сигнала с заданной спектральной плотностью……………………………………………8 6.5. Синтез оптимальных передаточных функций САУ при случайных воздействиях……………………….. 9 При изучении основ теории автоматического управления ранее предполагалось, что задающие и возмущающие воздействия представляют собой известные функции времени. Во многих практических случаях необходимо исследовать качество работы САУ, когда указанные выше воздействия являются случайными функциями, т.е. когда понятие о переходном процессе теряет смысл.
Это направление ТАУ основывается на методах теории случайных функций и математической статистики.
6.1. Случайные функции и их характеристики.
Функция, которая при каждом данном значении независимой переменной является случайной величиной, называется случайной функцией. Cлучайные функции, для которых независимой переменной является время, часто называют стохастическими процессами.
Основными характеристиками случайной функции (СФ) являются математическое ожидание 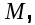 дисперсия дисперсия 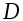 и корреляционная функция и корреляционная функция 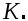
Математическое ожидание определяется выражением
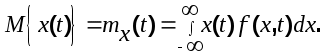 (6.1) (6.1)
Дисперсия
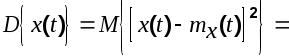
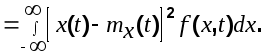 (6.2) (6.2)
Физический смысл понятия корреляционной функции заключается в определении вероятности того, что в момент времени 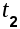 случайная функция примет значение случайная функция примет значение 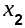 , если в момент , если в момент 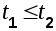 она получила значение она получила значение 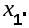
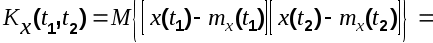 (6.3) (6.3)
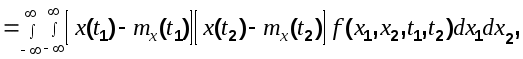
где 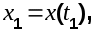 а а 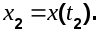
В приведенных выражениях:
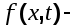 одномерный дифференциальный закон распределения, одномерный дифференциальный закон распределения,
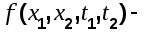 двумерный дифференциальный закон распределения. двумерный дифференциальный закон распределения.
В теории СФ математическое ожидание называют начальным моментом первого порядка, дисперсию-центральным моментом второго порядка, а корреляционную функцию - смешанным центральным моментом второго порядка. Раздел теории СФ, оперирующий только с моментами первых двух порядков, носит название корреляционной теории случайных функций.
Наиболее важным свойством СФ, определяющим возможность применения особых методов исследования, является зависимость или независимость свойств ее от начала отсчета времени. В соответствии с этим различаю
стационарные и нестационарные случайные функции. Для стационарных СФ все многомерные законы распределения зависят от взаимного расположения моментов времени 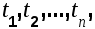 но не от самих значений этих величин (стационарность в узком смысле). Если этому условию удовлетворяют только моменты первых двух порядков то СФ называется стационарной в широком смысле. Процессы преобразования именно стационарных в широком смысле СФ системами автоматического управления мы и будем рассматривать, называя в дальнейшем эти СФ просто стационарными. но не от самих значений этих величин (стационарность в узком смысле). Если этому условию удовлетворяют только моменты первых двух порядков то СФ называется стационарной в широком смысле. Процессы преобразования именно стационарных в широком смысле СФ системами автоматического управления мы и будем рассматривать, называя в дальнейшем эти СФ просто стационарными.
По определению стационарной СФ ее математическое ожидание и дисперсия не зависят от времени, а корреляционная функция является функцией только промежутка времени 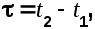 а не самих моментов отсчета времени. а не самих моментов отсчета времени.
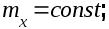 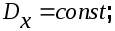
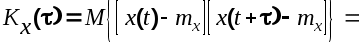
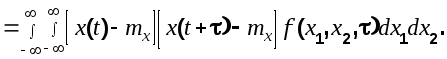 (6.4) (6.4)
Основные свойства корреляционной функции:
1.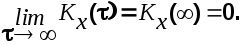
2.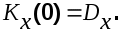
3.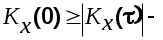 не возрастающая функция. не возрастающая функция.
4.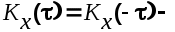 четная функция. четная функция.
Важной характеристикой стационарной СФ является ее спектральная плотность 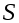 , которая связана с корреляционной функцией преобразованием Фурье. , которая связана с корреляционной функцией преобразованием Фурье.
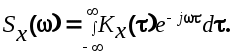 (6.5) (6.5)
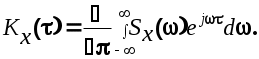 (6.6) (6.6)
Учитывая свойство 2, получим
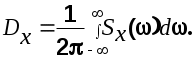 (6.7) (6.7)
Стационарный случайный процесс обладает эргодическим свойством. Это означает, что все его статистические характеристики могут быть определены по одной реализации достаточно большой длительности, либо по ансамблю относительно коротких реализаций.
В практических приложениях широкое распостранение получил стационарный случайный процесс типа “белый шум”,для которого
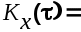 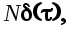 (6.8) (6.8)
где 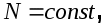 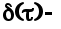 дельта-функция. дельта-функция.
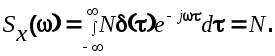 (6.9) (6.9)
Важное прикладное значение такого сигнала состоит в том, что анализ систем относительно случайных сигналов произвольной формы с помощью специальных формирующих фильтров можно заменить анализом относительно белого шума, что значительно упрощает решение задачи.
До сих пор мы рассматривали одну случайную функцию. Рассмотрим теперь в рамках корреляционной теории систему двух стационарных случайных функций 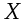 и и 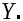 Так как первый и второй моменты каждой СФ в отдельности представляют собой уже изученные математические ожидания и корреляционные функции, то остается рассмотреть второй смешанный момент ординат различных СФ, взятых в различные моменты времени- так называемую взаимную корреляционную функцию. Так как первый и второй моменты каждой СФ в отдельности представляют собой уже изученные математические ожидания и корреляционные функции, то остается рассмотреть второй смешанный момент ординат различных СФ, взятых в различные моменты времени- так называемую взаимную корреляционную функцию.
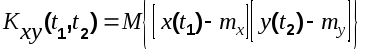
Eсли взаимная корреляционная функция зависит только от промежутка времени 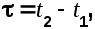 а не от самих моментов времени, то говорят, что указанные СФ стационарно связаны и их взаимную корреляционную функцию можно записать в следующем виде а не от самих моментов времени, то говорят, что указанные СФ стационарно связаны и их взаимную корреляционную функцию можно записать в следующем виде
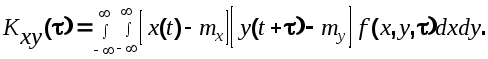 (6.10) (6.10)
Для взаимной корреляционной функции справедливо равенство
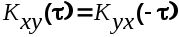 (6.11) (6.11)
Остальные свойства взаимной корреляционной функции аналогичны свойствам обычной, как часто говорят-автокорреляционной функции. Если к взаимной корреляционной функции применить преобразование Фурье, то получим взаимную спектральную плотность.
6.2.Связь между корреляционными функциями и спектральными плотностями величин на входе и выходе линейной динамической системы.
Пусть на вход САУ с передаточной функцией 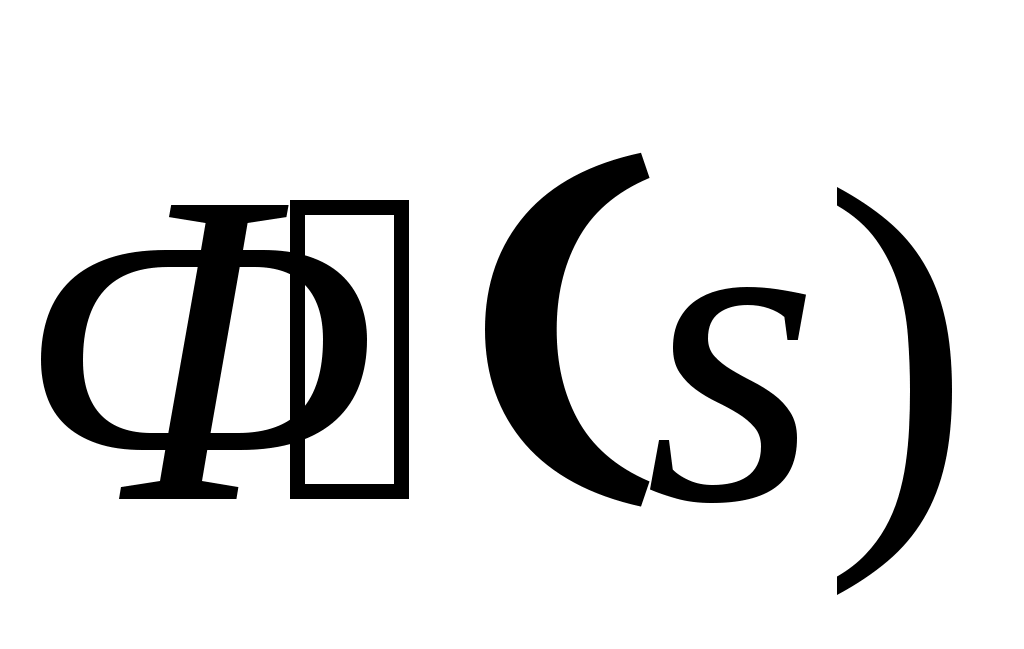 и функцией веса и функцией веса 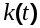 поступает случайный стационарный сигнал поступает случайный стационарный сигнал 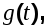 имеющий корреляционную функцию имеющий корреляционную функцию 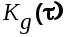 и спектральную плотность и спектральную плотность 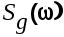 (рисунок 6.1). (рисунок 6.1).
Ф(s)
  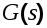  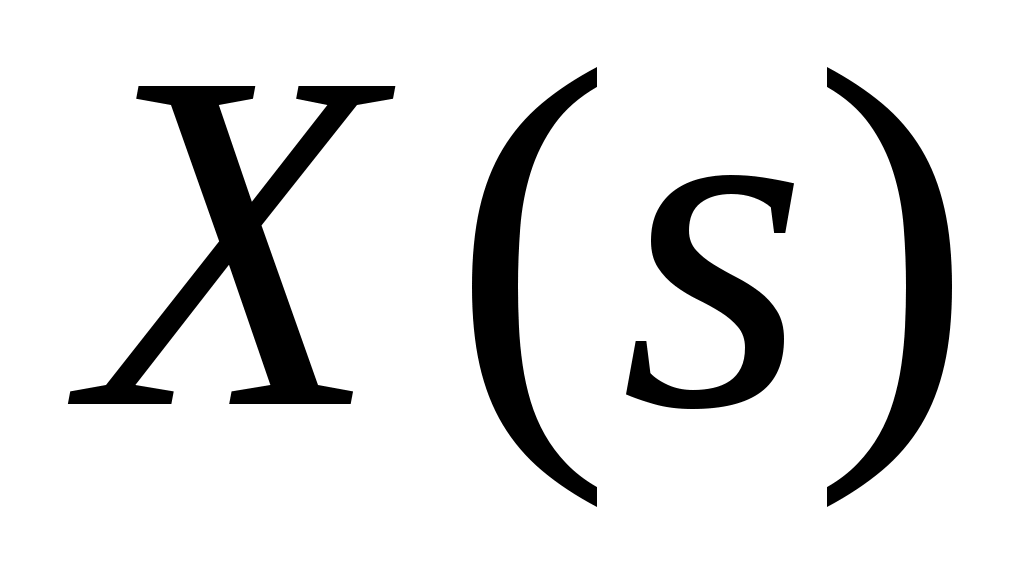
Рис.6.1. САУ при случайном воздействии на входе
Известно, что выходной сигнал определяется выражением
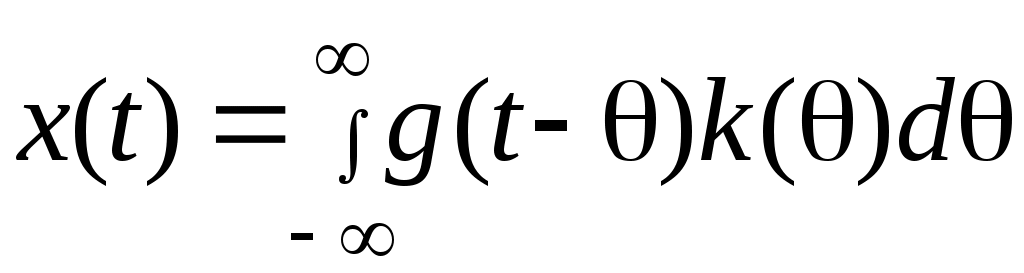 - (6.12) - (6.12)
Тогда математическое ожидание сигнала на выходе будет
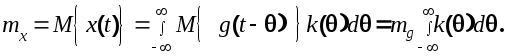
Так как функция веса является оригиналом передаточной функции, то в соответствии с теоремой о конечном значении оригинала получим
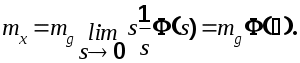 (6.13) (6.13)
Умножим обе части выражения (6.12) на 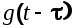
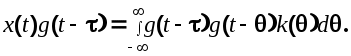
Применив к этому выражению операцию математического ожидания, получим
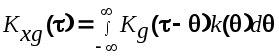 (6.14) (6.14)
Умножив обе части (6.12) на 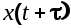 и применив снова операцию математического ожидания, можно записать и применив снова операцию математического ожидания, можно записать
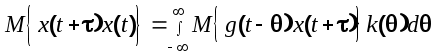 или или
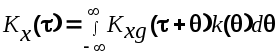 (6.15) (6.15)
Применив к выражению (6.14) преобразование Фурье, получим
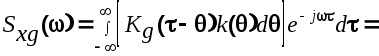
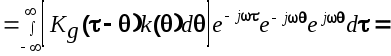
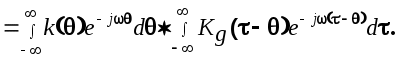
Отсюда
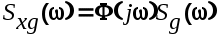 (6.16) (6.16)
С помощью преобразования Фурье, после аналогичных преобразований, из выражения (6.15) получим
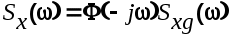 (6.17) (6.17)
Подставим (6.16) в (6.17) и будем иметь
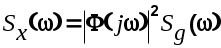 (6.18) (6.18)
Спектральная плотность сигнала на выходе линейной динамической системы равна спектральной плотности входного сигнала, умноженной на квадрат амплитудно-фазовой частотной характеристики системы.
Зная спектральную плотность, по выше приведенным формулам можно определить корреляционную функцию и дисперсию выходного сигнала.
6.3.Анализ динамической точности САУ.
Задача состоит в оценке динамической точности САУ, т.е. при непрерывно случайным образом изменяющихся воздействиях. Мерой динамической точности принято считать среднее квадратическое отклонение, которое определяется как
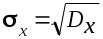 (6.19) (6.19)
Критерий минимума среднего квадратического отклонения (СКО) эффективен для широкого класса систем, но он не является универсальным, так как обеспечивает малое значение лишь средней, а не мгновенной ошибки. Поэтому в системах, где недопустимы большие, хотя и кратковременные ошибки, желательно задачу о целесообразном выборе передаточной функции системы решать не только на основе критерия минимума СКО, а с учетом ошибок в режиме переходного процесса.
Пусть на вход системы с передаточной функцией в разомкнутом состоянии 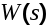 поступает полезный случайный сигнал поступает полезный случайный сигнал 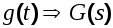 , имеющий спектральную плотность , имеющий спектральную плотность 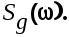

     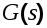 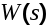 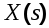

Рис 6.2. Система со случайным сигналом на входе
Передаточная функция системы по ошибке от задающего воздействия будет
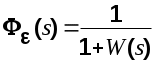
Cпектральная плотность ошибки определится как
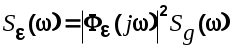 (6.20) (6.20)
Далее определяются дисперсия и СКО.
Cистема может находиться одновременно под воздействием двух случайных сигналов: полезного -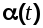 и возмущающего - и возмущающего - 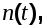 приложенных в одной точке, т.е. приложенных в одной точке, т.е. 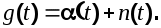 Очевидно, что в этом случае Очевидно, что в этом случае
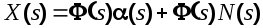
В данном случае передаточная функция замкнутой системы по возмущению совпадает с передаточной функцией по задающему воздействию. Ошибка системы определяется как разность между полезным (задающим) воздействием и управляемой величиной.
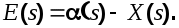
Отсюда
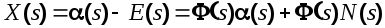
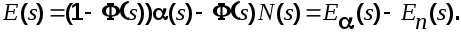
В этих выражениях
 составляющая ошибки от задающего воздействия; составляющая ошибки от задающего воздействия;
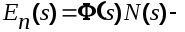 составляющая ошибки, вызванная помехой. составляющая ошибки, вызванная помехой.
Если полезный сигнал и помеха некоррелированны, то спектральная плотность ошибки будет
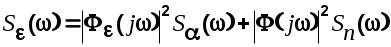 (6.21) (6.21)
Рассмотрим случай, когда задающее и возмущающее воздействия приложены различных точках (рис.6.3).
W1(s)
W2(s)
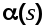      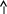   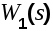  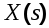
N(s)
 Рис. 6.3. Система с воздействиями в разных точках Рис. 6.3. Система с воздействиями в разных точках
Уравнения элементов системы в соответствии со схемой будут

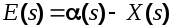
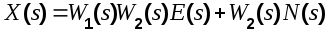
Определив из первого уравнения 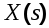 и подставив во второе, найдем и подставив во второе, найдем
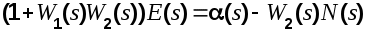
Отсюда
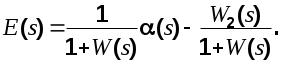
В этом выражении 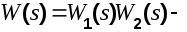 передаточная функция разомкнутой системы; передаточная функция разомкнутой системы;
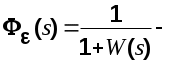 передаточная функция замкнутой САУ по ошибке от задающего воздействия. передаточная функция замкнутой САУ по ошибке от задающего воздействия.
Обозначим через 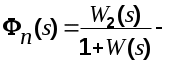 передаточную функцию замкнутой системы по помехе. Eсли полезный сигнал и помеха не коррелированы, то можно записать передаточную функцию замкнутой системы по помехе. Eсли полезный сигнал и помеха не коррелированы, то можно записать
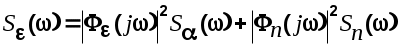 (6.22) (6.22)
Далее по прежнему следует вычисление дисперсии и СКО.
В практических приложениях вычисление интеграла вида
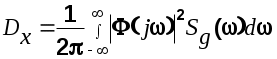
может вызвать существенные трудности. Для облегчения решения задачи от этот интеграл приводится к специальному табличному виду. Методика приведения и значения табличных интегралов приводятся в приложениях.
6.4. Формирование сигнала с заданной спектральной плотностью.
В ряде случаев теоретического и экспериментального исследования установившихся случайных процессов оказывается целесообразным свести приложенные к системе воздействия к одному и тому же типовому воздействию, в качестве которого выбирается белый шум.
Естественно, что при этом схема исследования должна быть преобразована таким образом, чтобы реализуемый ею установившийся случайный процесс 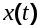 имел бы такие же значения характеристик (корреляционной функции,спектральной плотности и математического ожидания), которые совпадали бы с их реальными значениями. Преобразование это может быть осуществлено с помощью стационарного формирующего устройства, параметры которого должны выбираться так, чтобы образующийся на выходе его установившийся случайный процесс под влиянием приложенного ко входу белого шума обладал бы характеристиками реального входного воздействия. Схемы, поясняющие описанное преобразование показаны на рисунках 6.4a и 6.4b. имел бы такие же значения характеристик (корреляционной функции,спектральной плотности и математического ожидания), которые совпадали бы с их реальными значениями. Преобразование это может быть осуществлено с помощью стационарного формирующего устройства, параметры которого должны выбираться так, чтобы образующийся на выходе его установившийся случайный процесс под влиянием приложенного ко входу белого шума обладал бы характеристиками реального входного воздействия. Схемы, поясняющие описанное преобразование показаны на рисунках 6.4a и 6.4b.
  
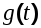        Ф(s) Ф(s) 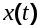  Ф(s) Ф(s) 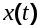
белый шум
Рис.6.4a. Случайный сигнал Рис.4b. Белый шум на входе
на входе системы формирующего фильтра
Так как спектральная плотность является четной дробно-рациональной функцией частоты, то она может быть представлена в виде двух комплексно-сопряженных сомножителей
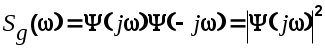  (6.23) (6.23)
Потребуем, чтобы спектральная плотность реального случайного сигнала была равна
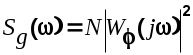 (6.24) (6.24)
Из (6.23) и (6.24) находится амплитудно-фазовая частотная характеристика формирующего фильтра
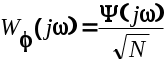 (6.25) (6.25)
Отметим, что установившиеся случайные процессы в реальной системе и в системе с формирующим устройством эквивалентны друг другу лишь по своим первым и вторым моментам и могут значительно различаться по моментам более высоких порядков. Однако, если воздействие в реальной системе и процесс на выходе формирующего устройства являются нормальными случайными функциями, то они полностью cоответствуют друг другу.
6.5.Синтез оптимальных передаточных функций САУ при случайных воздействиях.
Выше было показано,что если на входе системы помимо управляющего есть и возмущающее воздействие (помеха), то ошибка такой системы состоит из двух составляющих. Часто оказывается, что стремление уменьшить одну составляющую приводит к увеличению второй и наоборот. Задача синтеза и состоит в том, чтобы обеспечить минимально возможную сумму обеих составляющих.
Возможны несколько способов решения задачи синтеза. Первый и наиболее простой применим, если уже известна структура системы. В этом случае необходимо, используя выше приведенные выражения определить СКО как функцию варьируемых параметров системы и обычным методом определить их значения, дающие минимум ошибки. Еще один способ применим когда полезный сигнал имеет более низкочастотный спектр, чем помеха (рис.5).
   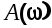 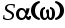 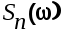

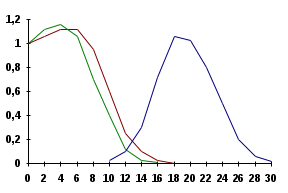 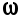
Рис.6.5. АЧХ системы спектральные плотности полезного сигнала
и помехи
В этом случае полоса пропускания системы должна быть выбрана достаточно широкой для обеспечения необходимой точности воспроизведения полезного сигнала, но такой ширины, чтобы полностью отфильтровать помехи.
В наиболее общем случае, когда спектры полезного сигнала и помехи накладываются друг на друга систему строят так, чтобы ее частотная характеристика максимально приближалась к спектральной характеристике полезного сигнала.
Рассмотрим методику определения оптимальной передаточной функции по критерию минимума СКО, когда структура системы неизвестна, а известна только передаточная функция неизменяемой части.
При определении оптимальной частотной характеристики замкнутой САУ 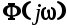 по критерию минимума СКО между идеальным сигналом по критерию минимума СКО между идеальным сигналом 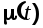 и оптимальным сигналом и оптимальным сигналом 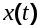 , предположим, что: , предположим, что:
1) идеальная частотная характеристика 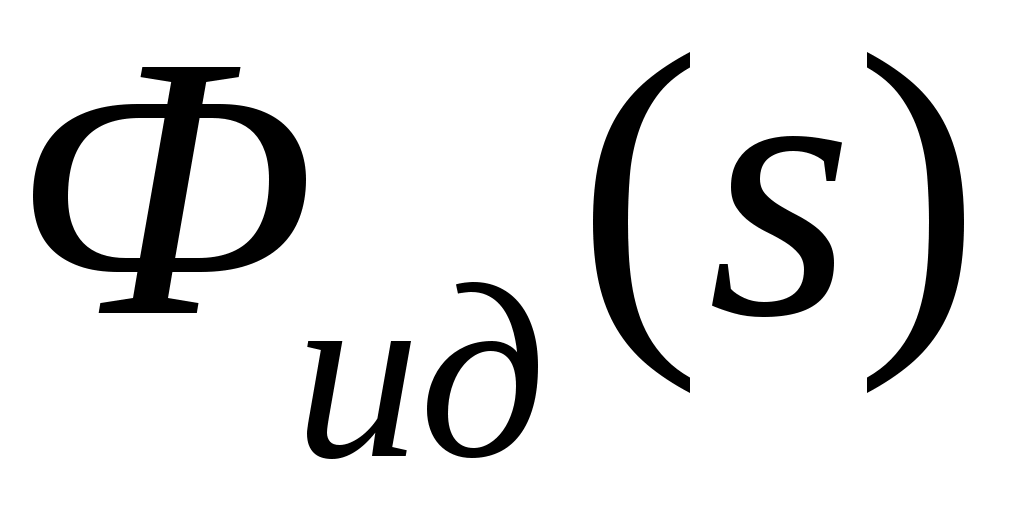 или идеальная функция веса или идеальная функция веса 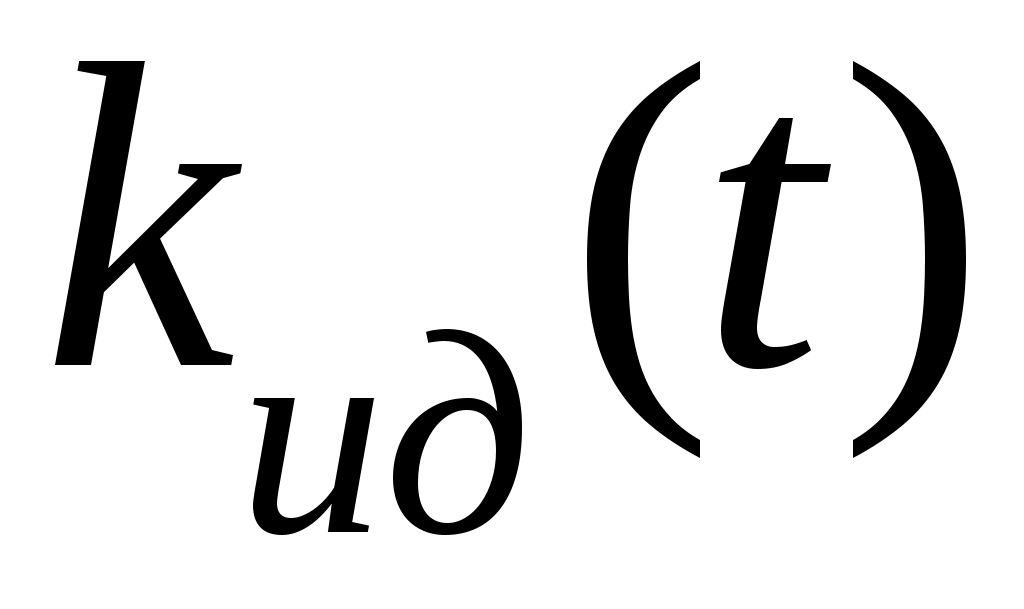 известны; известны;
2) полезный сигнал 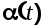 и помеха и помеха 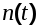 являются стационарными эргодическими случайными процессами с нулевым математическим ожиданием и их корреляционные функции и спектральные плотности известны; являются стационарными эргодическими случайными процессами с нулевым математическим ожиданием и их корреляционные функции и спектральные плотности известны;
3) на время переходного процесса ограничения не накладываются, т.е. решение ищется в классе систем с “ бесконечной памятью”.
Схема постановки задачи приведена на рисунке 6. 6.
Фид(s)
kид(t)
    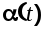  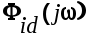 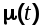
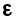 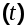
 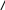  
Ф(s)
k(t)
 - -
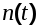     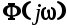
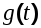 x(t) x(t)
Рис.6.6. Cхема синтеза оптимальной САУ 
Необходимое условие, которому должна удовлетворять оптимальная импульсная переходная функция 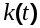 получена Н.Винером в виде интегрального уравнения получена Н.Винером в виде интегрального уравнения
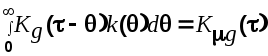 (6.26) (6.26)
при 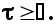
Корреляционная функция суммарного сигнала на входе определяется выражением
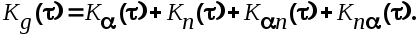
Условие 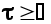 отражает принцип физической осуществимости системы. Если полезный сигнал и помеха некоррелированы, то отражает принцип физической осуществимости системы. Если полезный сигнал и помеха некоррелированы, то
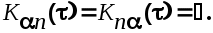
Уравнение (26) можно преобразовать к виду
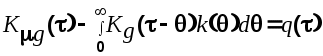 , (6.27) , (6.27)
где 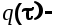 некоторая функция, равная нулю при некоторая функция, равная нулю при 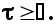 Это условие приводит к тому, что функция Это условие приводит к тому, что функция 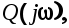 связанная с связанная с 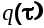 преобразованием Фурье, не будет содержать полюсов в верхней полуплоскости плоскости преобразованием Фурье, не будет содержать полюсов в верхней полуплоскости плоскости 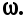 Преобразование Фурье дает возможность перейти к спектральным плотностям. Преобразование Фурье дает возможность перейти к спектральным плотностям.
 (6.28) (6.28)
Предположим, что спектральная плотность входного сигнала имеет дробно-рациональный вид и может быть представлена в виде
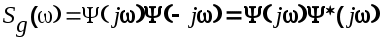 (6.29) (6.29)
Здесь 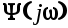 имеет все нули и полюсы в верхней полуплоскости, а имеет все нули и полюсы в верхней полуплоскости, а 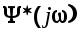 -в нижней полуплоскости плоскости -в нижней полуплоскости плоскости 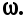 Разделим (6.28) на Разделим (6.28) на 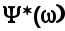 и получим и получим
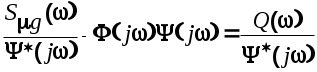 (6.30) (6.30)
Дробь в левой части выражения (6.30) можно преобразовать к виду суммы
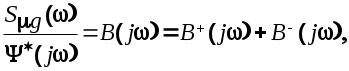 причем причем 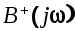 имеет все нули и полюсы только в верхней полуплоскости, а имеет все нули и полюсы только в верхней полуплоскости, а 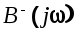 -только в нижней полуплоскости плоскости . С учетом этого выражение (6.30) преобразуем к виду -только в нижней полуплоскости плоскости . С учетом этого выражение (6.30) преобразуем к виду
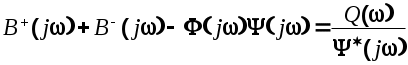
Последнее выражение справедливо для всей плоскости . Однако, поскольку необходимо выполнение условия физической реализуемости 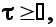 то решение ищется только в верхней полуплоскости и указанное выражение принимает вид то решение ищется только в верхней полуплоскости и указанное выражение принимает вид
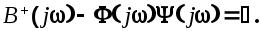
Отсюда для амплитудно-фазовой характеристики замкнутой САУ получим
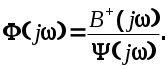 (6.31) (6.31)
Передаточная функция замкнутой САУ 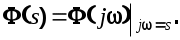 По этой передаточной функции определяется передаточная функция разомкнутой системы, а затем, с учетом известной передаточной функции неизменяемой части, находится передаточная функция корректирующего устройства. По этой передаточной функции определяется передаточная функция разомкнутой системы, а затем, с учетом известной передаточной функции неизменяемой части, находится передаточная функция корректирующего устройства.
Пример.
Полезный сигнал и помеха заданы своими корреляционными функциями:
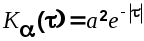 ; ; 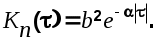
Полезный сигнал и помеха не коррелированы. Идеальная передаточная функция 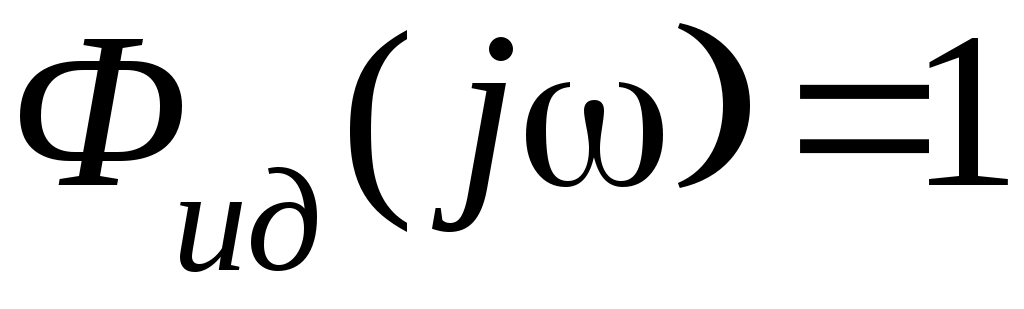 ,т.е. должна быть решена задача оптимальной фильтрации. ,т.е. должна быть решена задача оптимальной фильтрации.
Прежде всего определим спектральные плотности.
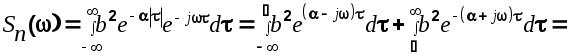
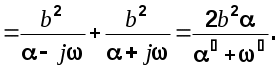
Аналогично получим
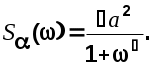
Далее процесс решения задачи Винера состоит из следующих операций:
1.Вычислим
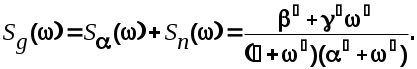
Здесь 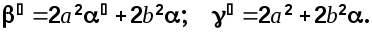
Разложим эту функцию на комплексно-сопряженные множители
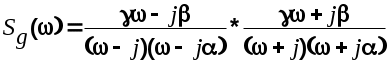
Отсюда
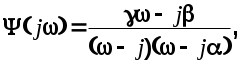
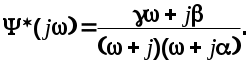
2. Вычислим взаимную спектральную плотность
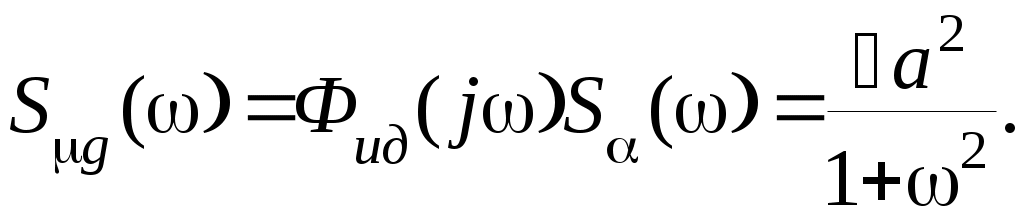 Ф Ф
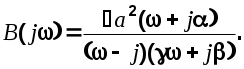
3. Определим функцию 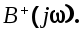
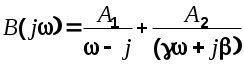
Приведя к общему знаменателю и приравнивая числители этого и предыдущего выражений, получим систему уравнений, из решения которой будем иметь
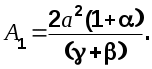
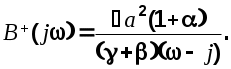
4. Вычислим частотную характеристику оптимальной системы
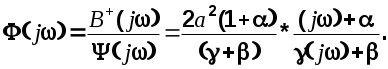 |
|
|
 Скачать 486.5 Kb.
Скачать 486.5 Kb.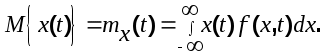 (6.1)
(6.1)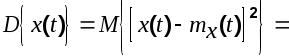
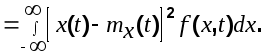 (6.2)
(6.2)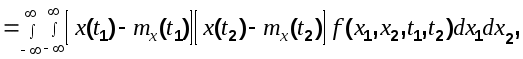
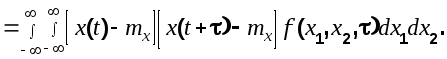 (6.4)
(6.4)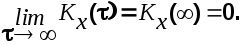
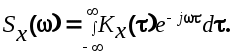 (6.5)
(6.5)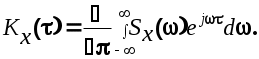 (6.6)
(6.6)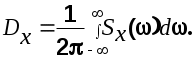 (6.7)
(6.7)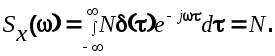 (6.9)
(6.9)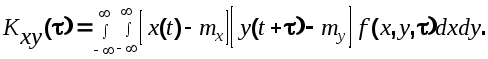 (6.10)
(6.10)

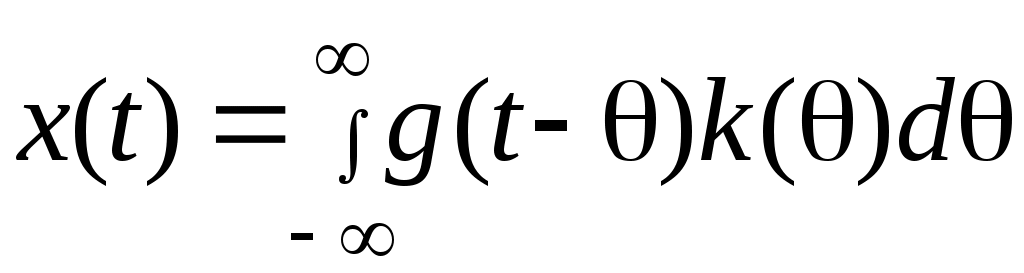 - (6.12)
- (6.12)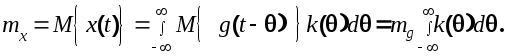
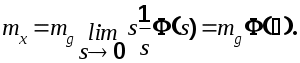 (6.13)
(6.13)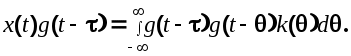
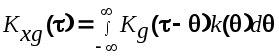 (6.14)
(6.14)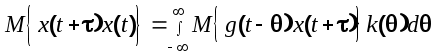 или
или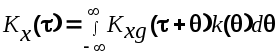 (6.15)
(6.15)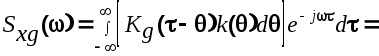







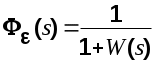




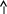



 Рис. 6.3. Система с воздействиями в разных точках
Рис. 6.3. Система с воздействиями в разных точках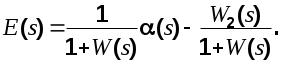
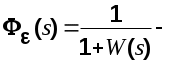 передаточная функция замкнутой САУ по ошибке от задающего воздействия.
передаточная функция замкнутой САУ по ошибке от задающего воздействия.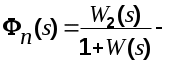 передаточную функцию замкнутой системы по помехе. Eсли полезный сигнал и помеха не коррелированы, то можно записать
передаточную функцию замкнутой системы по помехе. Eсли полезный сигнал и помеха не коррелированы, то можно записать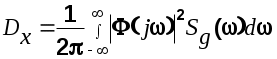





 Ф(s)
Ф(s) 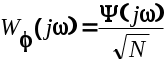 (6.25)
(6.25)







 -
- 


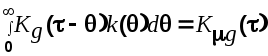 (6.26)
(6.26)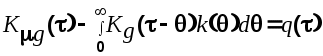 , (6.27)
, (6.27)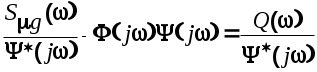 (6.30)
(6.30)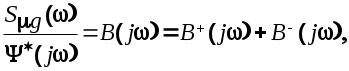 причем
причем 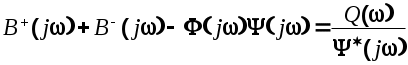
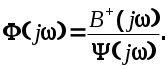 (6.31)
(6.31)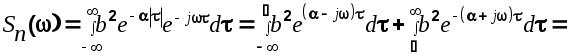
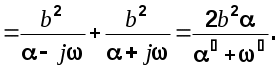
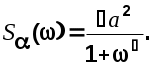
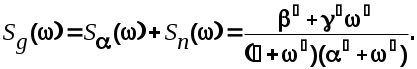
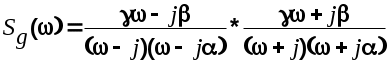
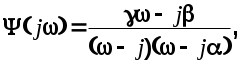
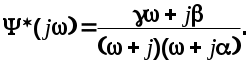
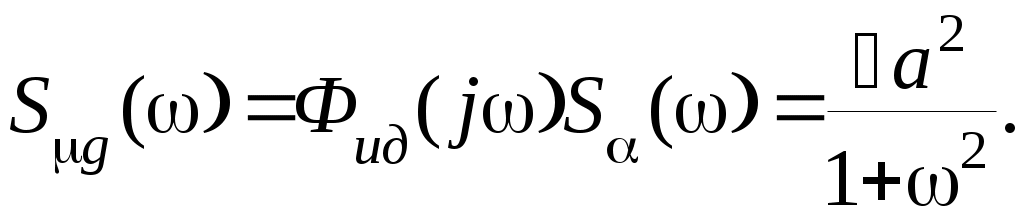 Ф
Ф