Кадровое агентство. Практическая округление чисел (1). Округление чисел в процессе вычислений
 Скачать 43.47 Kb. Скачать 43.47 Kb.
|
|
Практическое занятие №4 Тема: "Округление чисел в процессе вычислений" Цель работы: Используя теоретический материал и образцы решения задач, решить примеры по теме «Элементы теории погрешностей». Краткие теоретические сведения. Приближенное число заменяет собой число точное, которое чаще всего остается неизвестным. Верной цифрой называют такую, погрешность которой не превышает половины единицы следующего разряда. Сомнительная цифра – это цифра, следующая за верной. Значащими цифрами данного числа называют цифры, начиная с первой слева, отличной от нуля, и кончая последней, за точность которой еще можно поручиться. Погрешностью 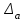 приближенного значения а числа х называется разность приближенного значения а числа х называется разность 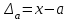 , а модуль этой погрешностью называется абсолютной погрешностью. , а модуль этой погрешностью называется абсолютной погрешностью.Если 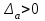 , то а взято с недостатком. Если , то а взято с недостатком. Если 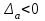 , то а взято с избытком. , то а взято с избытком.Границей погрешности приближенного значения а числа х называется всякое неотрицательное число 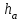 , которое не меньше модуля погрешности: , которое не меньше модуля погрешности: 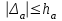 . .Говорят, что приближение а приближает число х с точностью до 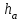 , если , если 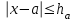 , , 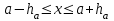 , , 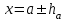 . .Относительной погрешностью приближенного значения а числа х называется отношение 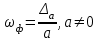 . .Квадратный корень из приближенного числа вычисляется по формуле: 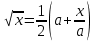 , где , где 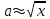 . .Общая формула для вычисления корня n-ой степени: 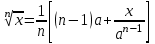 , где , где 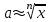 . .Пример 1.Округлить сомнительные цифры числа 72,353(±0,026) , оставив верные знаки в узком смысле. Решение. Пусть 72, 353 (±0, 026)=a . Согласно условию, погрешность a = 0, 026<0, 05;это означает, что в числе72,353верными в узком смысле являют- ся цифры 7, 2, 3. По правилам округления найдем приближенное значение числа, сохранив десятые доли: a1=72, 4;αa1=αa+ ∆окр=0, 026+0, 047=0, 073. Полученная погрешность больше 0,05; значит, нужно уменьшить число цифр в приближенном числе до двух: a2=72;αa2=αa+ ∆окр=0, 026+0, 353=0, 379. Так как αa2< 0, 5 , то обе оставшиеся цифры верны в узком смысле. Пример 2.Округлить сомнительные цифры числа 2,3544;δ=0,2% , оставив верные знаки в широком смысле. Решение. Пустьa=2, 3544;δa=0, 2%;тогдаαa=a⋅δa=0, 00471.В данном числе верными в широком смысле являются три цифры, поэтому округляем его, сохраняя эти три цифры: a1=2, 35;αa1=0, 0044+0, 00471=0, 00911<0, 01. Значит, в округленном числе 2,35 все три цифры верны в широком смысле. Порядок проведения работы: 1. Используя теоретические сведения, выполнить предложенное преподавателем задание. 2. Соответствующим образом оформить работу Перечень заданий. Округлить сомнительные цифры числа, оставив верные знаки: а) в узком смысле; б) в широком смысле. Определить абсолютную погрешность результата.
Содержание отчета Отчет должен содержать: 1.Название работы 2.Цель работы 3.Задание 4.Формулы расчета 5.Результат | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
