Современные системы компьютерной алгебры. отчет. Описать особенности реализации алгебраических структур в ска

• Название: Описать особенности реализации алгебраических структур в ска
• Анкор: Современные системы компьютерной алгебры
• Дата: 27.12.2021
• Размер: 141.33 Kb.
• Имя файла: отчет.docx
• Тип: Документы; #319989

Введение

В данной работе рассматриваются вопросы изучения, а также применения современных систем компьютерной алгебры при решении исследовательских задач. В процессе выполнения работы необходимо решить следующие задачи:

1. 
   Изучить представление алгебраических структур в СКА.
   
2. 
   Описать особенности реализации алгебраических структур в СКА.
   
3. 
   Изучить существующие генераторы битовых последовательностей и последовательностей целых чисел. Обосновать актуальность исследования псевдослучайных последовательностей и методов их построения.
   
4. 
   Реализовать мультипликативный генератор Фибоначчи с запаздыванием, генерирующий последовательность, элементами которой являются элементы множества (p – простое число). В качестве умножения матриц использовать умножение, обеспечивающее выполнение аксиом кольца.
   
5. 
   Провести исследование периодов последовательностей, вырабатываемых генератором, реализованным в пункте
   
6. 
   Найти закономерности и сделать выводы.
   

1 Алгебраические структуры в СКА

1.1 Характеристика систем компьютерной алгебры

Направление «компьютерная алгебра» представлено теорией, технологиями, программными средствами. К прикладным результатам относят разработанные алгоритмы и программное обеспечение для решения с помощью компьютера задач, в которых исходные данные и результаты имеют вид математических выражений, формул. Основным продуктом компьютерной алгебры стали программные системы компьютерной алгебры – СКА (англ. Computer Algebra System, CAS).

Основное назначение СКА – работа с математическими выражениями в символьной форме. Базовые типы данных СКА: числа и математические выражения. Числа: короткие и длинные целые (одинарной и кратной точности), рациональные, комплексные, алгебраические числа. Алгебраическое число задается своим минимальным многочленом, а иногда для его задания требуется указать интервал на прямой или область в комплексной плоскости, где содержится единственный корень данного многочлена. Математические выражения: арифметика, функции, уравнения, производные, интегралы, векторы, матрицы, тензоры. Кроме того, в компьютерной алгебре рассматриваются такие объекты, как: функциональные, дифференциальные поля, допускающие показательные, логарифмические, тригонометрические функции; матричные кольца и другие.

СКА работают следующим образом [7]:

– математические объекты (алгебраические выражения, ряды, уравнения, векторы, матрицы и др.) и указания, что с ними делать, задаются пользователем на входном языке системы в виде символьных выражений;

– интерпретатор анализирует и переводит символьные выражения во внутреннее представление;

– символьный процессор системы выполняет требуемые преобразования или вычисления и выдает ответ в математической нотации. Алгоритмы внутренних преобразований имеют алгебраическую природу, что и отражено в названии систем – системы компьютерной алгебры. Содержание техники символьных вычислений;

– внутреннее представление математического выражения в системе символьных вычислений – синтаксическое дерево (список списков);

– суть символьных вычислений (аналитических преобразований) – переписывание терма с помощью последовательного применения правил из определённого пользователем или системой списка;

– преобразование из внешнего представления во внутреннее и обратно обеспечивается дополнительными инструментальными средствами.

Многие выделяют СКА общего назначения и специализированные. Наиболее известные системы из первой группы: Derive, Mathematica, Maple, Macsyma и еѐ потомок Maxima, Scratchpad и еѐ потомок Axiom, Reduce, MuPAD, Mathcad, MATLAB, Sage, SMath Studio, Yacas, Scientific WorkPlace, Kalamaris. Системы для решения задач одного или нескольких смежных разделов символьной математики – это специализированные СКА. Примерами таковых являются: GAP (теория групп), Cadabra (тензорная алгебра), KANT (алгебра и теория чисел), Singular (полиномиальные вычисления с акцентом на нужды коммутативной алгебры, алгебраическая геометрия), Calc3D (для работы с 3D матрицами, векторами, комплексными числами), GRTensorII (дифференциальная геометрия). Классификация СКА по типу архитектуры является, скорее следствием истории становления, потому что у большинства на современном этапе структуры одинаковые. Отличительным признаком является – используется собственное ядро или заимствовано от других. Более того, у 9 некоторых изначально было ядро одного производителя, потом перешли на другое. Например, у Mathcad символьные вычисления выполнялись на базе сокращѐнного ядра системы Maple, начиная с 14 версии, используется символьное ядро MuPAD [7].

1.2 Понятие алгебраических структур

Алгебраическая структура – это множество   с заданным на нём набором операций и отношений, удовлетворяющим некоторой системе аксиом [4].

Группа – моноид , все элементы которого обратимы. Другими словами, предполагаются выполненными следующие аксиомы:

G0) на множестве G определена бинарная операция

G1) операция ассоциативна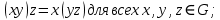

G2) обладает нейтральным (единичным) элементом для всех

G3) для каждого элемента 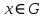существует обратный [4].

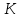Пусть – не пустое множество, на котором заданы две операции сложение и умножение, удовлетворяющие следующим условиям:

К1) ( ,+) – абелева группа;

К2) ( ,*) – полугруппа;

К3) операции сложения и умножения связаны дистрибутивными законами




для всех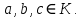

Тогда называется кольцом [4].

Поле 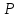– это коммутативное кольцо с единицей в котором каждый элемент [4].

1.3 Реализация конечных колец, полей, векторных пространств квадратных матриц над конечными полями в системе Sage

Рассмотрим, как можно реализовать работу с конечными кольцами, полями, а также элементами векторного пространства в системе Sage.

Конечное кольцо можно задать следующим образом.

Сначала задаём кольцо целых чисел, затем его идеал, образованный с помощью какого – либо элемента кольца, а затем факторизацию кольца целых чисел по идеалу K:
sage: K=ZZ; I=K.ideal(14)

sage: L=K.quotient_ring(I)
Итак, в мы получили конечное кольцо, элементы которого можно отождествить с остатками от деления на целое число 14.

Можно просмотреть в таком виде все элементы кольца с помощью следующего набора команд:
sage: for x in L:

print(x)

В результате получим:
0

1

2

3

4

5

6

7

8

9

10

11

12

13

Можно выяснить, является ли построенное кольцо полем с помощью команды L.is_field(). В результате получим «True», что означает, что построенное кольцо является полем.

Если нужно построить и просмотреть таблицу сложения элементов построенного кольца, то можно ввести следующие команды:
sage: ms=L.addition_table(names='elements'); print(ms)

Результат представлен на рисунке 1.



Рисунок 1 – Таблица сложения элементов построенного кольца
Если нужно построить и просмотреть таблицу умножения элементов построенного кольца, то можно ввести следующие команды:
sage: mt=L.multiplication_table(names='elements'); print(mt)
Результат представлен на рисунке 2.

Рисунок 2 – Таблица умножения элементов построенного кольца
Рассмотрим, как можно в Sage работать с произвольными конечными полями.

Далее представлен код, который реализует конечное поле (поле Галуа) GF(9) вместе с таблицами сложения и умножения элементов этого поля:
sage: F.=GF(2^3); M=F.list(); M
Поиск многочлена, на который делим.
sage: ms=F.addition_table(names='elements'); ms

sage: mt=F.multiplication_table(names='elements'); mt
В результате в Sage поле, элементы которого можно отождествить с многочленами, являющимися остатками при делении на многочлен.

Вид таблицы сложения элементов поля 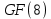представлен на рисунке 3.

Рисунок 3 – Вид таблицы сложения элементов поля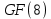
Вид таблицы умножения элементов поля 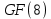представлен на рисунке 4.


Рисунок 4 – Вид таблицы умножения элементов поля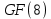
Рассмотрим, как задается векторное пространство над полем действительных чисел в Sage. Например, далее следует набор команд, задающий векторное пространство над полем действительных чисел.
sage: W=VectorSpace(RR,2)

sage: M=W.basis(); print(M); d=W.dimension(); print(d)
Матрицы фиксированного размера над полем сами образуют векторное пространство над этим полем. Его можно явно задать и после этого выполнять в нем все допустимые в векторных пространствах операции.

Далее в работе нам понадобится реализация матричного пространства с квадратными матрицами, элементами которых являются элементы конечного поля.

Пространство квадратных матриц размера 2х2 над конечным простым полем характеристики 7 можно задать так:
sage: M = MatrixSpace(GF(7),2,2)
Приведём пример того, как можно перемножать такие матрицы на примере квадратных матриц второго порядка.
sage: A = M([3,1, 2,0]);print("A="); print(A)

sage: B = M([1,2, 3,4]);print("B="); print(B)

sage: C= A*B

sage: print("C="); print(C)
Результат выполнения этих команд:

A=

[3 1]

[2 0]

B=

[1 2]

[3 4]

C=

[6 3]

[2 4]
Приведем пример кода, реализующего матричное пространство над полем Галуа GF(8) и пример умножения таких матриц.
sage: F.=GF(2^3)

sage: M = MatrixSpace(F,3,3)

sage: A = M.random_element();print("A="); print(A);print()

sage: B = M.random_element();print("B="); print(B);print()

print("AB="); print(A*B)
Результат выполнения этих команд представлен на рисунке 5:

Рисунок 5 – Результат умножения квадратных матриц в системе Sage

2 Индивидуальное задание

2.1 О генераторах последовательностей

Генератор псевдослучайных чисел – алгоритм, генерирующий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению. ГПСЧ, не используют внешних источников случайности, а формируют число только алгебраическими преобразованиями, поэтому получаемые числа нельзя называть случайными, именно из-за этого их называют псевдослучайными.

Использование ГПСЧ широко применимы, потому что элемент случайности может пригодиться в различных областях, например:

1. 
   игры и развлечения. В последнее время в видео играх часто применяется механика loot box, суть ее в создании «сундуков» со случайными предметами. Также псевдослучайные числа применимы для настройки поведения игровых персонажей.
   
2. 
   защита информации.
   
3. 
   моделирование физических явлений.
   

Случайное число – число, представляющее собой реализацию случайной величины [5].

Детерминированный алгоритм – алгоритм, который возвращает те же выходные значения при тех же входных значениях.

Псевдослучайное число – число, полученное детерминированным алгоритмом, используемое в качестве случайного числа.

Физическое случайное число (истинно случайное) – случайное число, полученное на основе некоторого физического явления.

Как правило, генерация случайного числа состоит из двух этапов:

1) генерация нормализованного случайного числа (то есть равномерно распределенного от 0 до 1);

2) преобразование нормализованных случайных чисел в случайные числа, которые распределены по заданному закону распределения или в необходимом интервале.

Генератор случайных бит (ГСБ) – это устройство или алгоритм, который выдает последовательность статистически независимых и несмещенных бит (то есть подчиняющихся закону распределения) [5].

Генератором псевдослучайных бит (детерминированным ГПСБ) будем называть детерминированный алгоритм 1, который получает на вход двоичную последовательность длины k и выдает на выходе двоичную последовательность длины ( 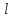значительно больше ), которая «выглядит случайной». Входное значение ГПСБ называется начальным вектором (также называют инициализационным вектором и обозначают IV), а выход называется псевдослучайной последовательностью бит [5].

Алгоритмический генератор является комбинацией физического генератора и детерминированного алгоритма. Такой генератор использует ограниченный набор данных, полученный с выхода физического генератора для создания. Генераторы псевдослучайных чисел длинной последовательности чисел преобразованиями исходных чисел. Данный вид генераторов представляет наибольший интерес в силу его очевидных преимуществ над генераторами случайных чисел других видов [5].

Традиционные генераторы псевдослучайных последовательностей строятся на генераторах, основанных на линейных конгруэнтных методах, а также использующие идею построения последовательностей Фибоначчи.

Рассмотрим основные идеи построения таких генераторов.

Общая схема линейных конгруэнтных генераторов была предложена Д.Г. Лехмером в 1949 году.

Сформулируем последовательность { } такую, что
,
или, обобщая:
.
Эта последовательность называется линейной конгруэнтной последовательностью. Максимальный период такой последовательности равен .

Полиномиальный конгруэнтный генератор, уравнение работы которого имеет вид
.
Максимальный период такой последовательности равен .

Аддитивный генератор Фибоначчи и аддитивный генератор Фибоначчи с запаздыванием, уравнения работы которых имеют соответственно вид
и ,
где – четное.

Дж. Марсалья предложил заменить сложение в формуле для аддитивного генератора умножением, получив тем самым мультипликативный генератор Фибоначчи с запаздыванием:
,
где – чётное, а – целые нечетные числа, сравнимые с 1 по модулю 4.

Инверсивный конгруэнтный генератор, уравнение работы которого имеет вид
,
где – простое число, [9, с.27].


2.2 Реализация мультипликативного генератора Фибоначчи с запаздыванием, генерирующего последовательности, элементами которых являются элементы множества (p – простое число)


В результате изучения литературы по генераторам псевдослучайных последовательностей можно сделать вывод, что наиболее исследованы генераторы псевдослучайных битовых и числовых последовательностей. Современные разработки направлены в сторону иных математических объектов, изучение которых нацелено на поиск способов улучшения широко известных генераторов. Например, в качестве таких объектов рассматриваются точки эллиптических кривых [6-8], элементы групп подстановок [1], элементы колец Галуа [3] и другие.

Будем рассматривать в качестве элементов последовательностей матрицы над конечными полями.

Построим мультипликативный генератор Фибоначчи, с помощью которого можно будет получать последовательность, элементами которой являются элементы множества (p – простое число). В качестве умножения матриц будем рассматривать использовать скобку Ли.

По аналогии с числовым мультипликативным генератором Фибоначчи с запаздыванием, определим мультипликативный генератор Фибоначчи с запаздыванием, вырабатывающий квадратные матрицы с элементами из простого конечного поля, определим с помощью рекуррентного соотношения вида

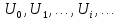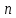где – целые числа, – квадратные матрицы порядка . Элементами матриц являются элементы простого конечного поля GF(p). Каковы аналогичные числовым ограничения на начальные матрицы, авторам работы пока не известно.

Определённый таким образом генератор реализован в системе компьютерной алгебры Sage. Он реализован в виде программы, позволяющей получать последовательности по описанным рекуррентным соотношениям и находить соответствующие им периоды.
sage: p=7; n=3; t=20; k=10000; l=100000

sage: M = MatrixSpace(GF(p),n,n)

sage: z = []

sage: for r in range(t):

U = M.random_element();print("U0="); print(U);print()

V = M.random_element();print("U1="); print(V);print()

for i in range(k):

W = U*V; U=V; V=W

W = U*V; U=V; V=W; X=W

W = U*V; U=V; V=W; Y=W

s=1;b=false;

for j in range(k+1,l):

W = U*V

if (V==X) and (W==Y):

b=true; break;

W = U*V; U=V; V=W;s=s+1

if b:

print("Период равен ", s); print(); z.append(s)

if b==false:

print("Период не найден"); print(); z.append(0)

sage: print(); print("Массив найденных периодов"); print(z)

sage: print("Максимальное значение периода ", max(z))

sage: print("Минимальное значение периода ", min(z))

2.3 Исследование периодов последовательностей мультипликативного генератора Фибоначчи

Проведём исследование реализованного в пункте 2.2 генератора. В ячейках таблицы 1 представлены максимальные значения периодов, которые удалось достичь при случайной генерации последовательностей. Выбор максимально возможного периода происходил как наибольшего числа из полученных периодов.

Одной из наиболее значимых характеристик генераторов является значение максимальных периодов вырабатываемых ими последовательностей. Мы исследовали получающиеся возможные максимальные значения периодов последовательностей.


Таблица 1 – Результаты нахождения максимально возможных значений периода последовательности

p	n=2		n=3		n=4		n=5		n=6
	min	max	min	max	min	max	min	max	min	max
2	1	8	1	128	1	3276	1	157604	1	1963920
3	1	48	1	3432	1	262320	6	3804096	–	–
5	1	150	1	60636	4	3286992	–	–	–	–
7	1	1176	1	202920	–	–	–	–	–	–

Для изучения характера зависимости максимальных периодов от характеристик полей нами построены графики этих зависимостей, которые представлены далее на рисунках 6-9.

Рисунок 6 – График зависимости максимальных значений периода от порядков матриц при

Рисунок 7 – График зависимости максимальных значений периода от порядков матриц при

Рисунок 8 – График зависимости максимальных значений периода от порядков матриц при

Рисунок 9 – График зависимости максимальных значений периода от порядков матриц при
По результатам изучения максимально возможных периодов последовательностей, реализованных в СКА можно сделать вывод, что мощности онлайн системы не хватает для полноценного исследования генератора данного типа. Так, например, не удается найти периоды, уже начиная с . В процессе исследования было замечено, что при выбранной размерности поля максимальный период возрастает на всей размерности поля. Можно выдвинуть гипотезу о том, что зависимости носят экспоненциальный характер.

Таким образом, частично удалось выявить зависимость роста значений периода зависимости от характеристик поля и размерности матриц. Для улучшения представлений о характере этих зависимостей необходимо проводить дальнейшие исследования с помощью инструментов высокопроизводительных вычислений.

Заключение

По результатам выполнения поставленных в работе задач можно сделать следующие выводы.

Первая задача, поставленная в данной работе, заключалась в том, чтобы, изучить представление алгебраических структур в СКА. В результате изучены источники по различным СКА и перечислены их возможности для представления алгебраических структур.

Вторая задача, сформулированная в работе, предполагала сделать описание особенностей реализации алгебраических структур в СКА. В работе представлено изучение Sage. Для выполнения практических заданий практики выбрана система Sage, так как она позволяет программировать, используя основные конструкции языка программирования Python.

Третья задача работы заключалась в реализации работы с конечными кольцами и полями, векторными пространствами квадратных матриц над конечными полями в выбранной СКА Sage. Рассмотрены функции, позволяющие осуществлять работу с конечными кольцами, полями, а также векторными пространствами матриц над конечными полями.

Изучить существующие генераторы битовых последовательностей и последовательностей целых чисел и обосновать актуальность исследований псевдослучайных последовательностей и методов их построения стало четвёртой задачей работы. В результате изучены существующие генераторы, особенности их создания, работы и применения на практике и установлено, что данная тема является актуальной, так как при реализациях алгоритмов существующих генераторах остаются проблемы.

Пятая задача связана с реализацией мультипликативного генератора Фибоначчи с запаздыванием, генерирующего последовательность, элементами которой являются элементы множества (p – простое число). В качестве умножения матриц использовать умножение, обеспечивающее выполнение аксиом кольца. В программной среде Sage реализован данный мультипликативный генератор Фибоначчи с запаздыванием. Программа позволяет не только находить элементы последовательностей, но и периоды генерируемых последовательностей, выбирать максимальный и минимальный значения периодов из всех периодов сгенерированных последовательностей.

Шестая заключалась в проведении исследования периодов последовательностей, создаваемых реализованным генератором. В результате была частично выявлена закономерность между значениями характеристик поля, порядка квадратных матриц и максимально достигаемым периодом.

Список использованных источников

1. 
   Бахта, Н.С. Методы построения псевдослучайных последовательностей элементов групп / Н.С. Бахта, Н.А. Попова // Вестник ОмГУ. – 2014. – №2 (72). – С. 15-16.
   
2. 
   Иванов, М.А. Теория, применение и оценка качества генераторов псевдослучайных последовательностей / М.А. Иванов, И.В. Чугунков. – Москва: КУДИЦ-ОБРАЗ, 2003. – 238 с.
   
3. 
   Камловский, О.В. Уточнение оценок для числа появлений элементов в линейных рекуррентных последовательностях над кольцами Галуа / О.В. Камловский // Фундаментальная и прикладная математика. – 2012. – 17:7. – С. 97-115.
   
4. 
   Кострикин, А.И. Введение в алгебру. Часть 1. Основы алгебры: Учебник для вузов / А.И. Кострикин. – М.: Физико-математическая литература, 2000. – 272 с.
   
5. 
   Слеповичев, И.И. ГЕНЕРАТОРЫ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ: учебное пособие / И.И. Слеповичев – 2017. – 118 с.
   
6. 
   Тараканов, В.Е. Линейные рекуррентные последовательности на эллиптических кривых и их применение в криптографии / В.Е. Тараканов // Труды по дискретной математике. – 2006. – Т. 9. – С. 340-356.
   
7. 
   Таранчук, В.Б. Основные функции систем компьютерной алгебры: пособие для студентов фак. прикладной математики и информатики / В.Б. Таранчук. – Минск: БГУ.­ – 2013. – 59 с.
   
8. 
   Червяков, Н.И. Реализация EC-последовательностей на точках эллиптической кривой с использованием нейронных сетей / Н.И. Червяков, М.Г. Бабенко, А.С. Назаров, И.С. Крисина // Высокопроизводительные параллельные вычисления на кластерных системах. Материалы XIII Всероссийской конференции (Н. Новгород, 14–16 ноября 2013 г.) – Нижний Новгород: Изд-во Нижегородского госуниверситета. – 2013. – С. 274–278.
   
9. 
   Иванов,М.А.Теория, применение и оценка качества генераторов псевдослучайных последовательностей / М.А. Иванов, И.В. Чугунков. – М.: КУДИЦ-ОБРАЗ, 2003. – 238 с.
   
10. 
    Калядин, В.П. Алгебраические структуры: Электронное учебное пособие / В.П. Калядин – Самара: Издательство «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С.П.КОРОЛЕВА (НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)», 2011. – 70 c..
    
11. 
    Малакаев, М.С. Основы работы с системой компьютерной алгебры Maxima: Учебно-методическое пособие / М.С. Малакаев, Л.Р. Секаева, О.Н. Тюленева. – К.: Казанский университет, 2012. – 57 с.
    
12. 
    Панкратьев, Е.В. Элементы компьютерной алгебры: учебник / Е.В. Панкратьев; Национальный Открытый Университет «ИНТУИТ». – М.: Интернет-Университет Информационных Технологий (ИНТУИТ): Бином. Лаборатория знаний, 2007. – 247 с.
    
13. 
    Мещеряков, В.В. Задачи по математике с MATLAB & Simulink: учебное пособие: [16+] / В. В. Мещеряков. – М.: Диалог-МИФИ, 2007. – 528 с.
    
14. 
    Зобнин, А.И. Компьютерная алгебра в системе Sage: учебное пособие / А.И. Зобнин, О.В. Соколова – М.: Издательство МГТУ им. Баумана, 2011. – 55 с.
    
15. 
    Яцкин, Н.И. Алгебраические вычисления в системе Sage: Методические указания по дисциплинам «Фундаментальная алгебра» и «Компьютерная алгебра» для студентов 2 курса факультета математики и компьютерных наук (квалификация «Бакалавр») / Н.И. Яцкин. – Иваново: Издательство «Ивановский государственный университет», 2014. – 47 с.
    
16. 
    Документация по работе с Sage «Sage Tutorial in Russian» Выпуск 9.3 от 10.05.2021 [Электронный ресурс]. – Режим доступа: https://doc.sagemath.org/pdf/ru/tutorial/SageTutorial_ru.pdf
    
17. 
    L’Ecuyer, P. History of uniform random number generation / P. L'Ecuyer // Proceedings of the 2017 Winter Simulation Conference. – P. 202-230. –https://www.researchgate.net/publication/318318619_History_of_uniform_random_number_generation.