Главная страница
Навигация по странице:

  • Минимум и максимум

  • Среднее линейное отклонение (

  • среднеквадратическое отклонение

  • Частота встречаемости ( абсолютная частота )

  • X i 55 58 60 62

  • Пример.

    		•

    Описательная статистика (ручной расчёт). Описательная статистика


    Скачать 366 Kb.
    НазваниеОписательная статистика
    Дата04.03.2018
    Размер366 Kb.
    Формат файлаdoc
    Имя файлаОписательная статистика (ручной расчёт).doc
    ТипДокументы
    #37681

    ОПИСАТЕЛЬНАЯ СТАТИСТИКА.

    Цель занятия - максимально развить интуитивное и практическое представление об анализе данных, статистической обработке эксперимента, не предполагая наличия у них специальной подготовки. Познакомить с культурой анализа данных.

    Статистика позволяет компактно описать данные, понять их структуру, провести классификацию, увидеть закономерности в хаосе случайных явлений.

    Первый раздел математической статистики – описательная статистика – предназначен для представления данных в удобном виде и описания информации в терминах математической статистики и теории вероятностей.

    Медицинская статистика - это отраслевая статистика, комплекс методов прикладной статистики, которые применяются в научной, практической медицине и здравоохранении.

    Основные задачи медицинской статистики:

    - статистика рождаемости и смертности;

    - статистика заболеваемости;

    - статистика деятельности учреждений здравоохранения.

    Вместе описательная и аналитическая статистики решают следующую задачу:

    - сбор данных и описание их в удобном для статистической обработки виде;

    - обработка результатов методами теоретической (общей ) статистики;

    - анализ полученных результатов, прогнозирование, выработка оптимальных решений.

    Основной величиной в статистических измерениях является единица статистической совокупности. Единица статистической совокупности характеризуется набором признаков или параметров. Значения каждого параметра или признака могут быть различными и в целом образовывать ряд случайных значений x1, х2, …, хn.

    Переменная - это параметр измерения, который можно контролировать или которым можно манипулировать в исследовании. Так как значения переменных не постоянны, нужно научиться описывать их изменчивость.

    Для этой цели существует описательная или дескриптивная статистика.

    Идея описательной статистики очень проста: вместо того чтобы рассматривать все значения переменной, а их может быть очень много (тысячи и миллионы), вначале стоит просмотреть описательные статистики. Они дают общее представление о значениях, которые принимает переменная.

    Остановимся на основных понятиях описательной статистики.

    Минимум и максимум — это минимальное и максимальное значения переменной.

    Среднее (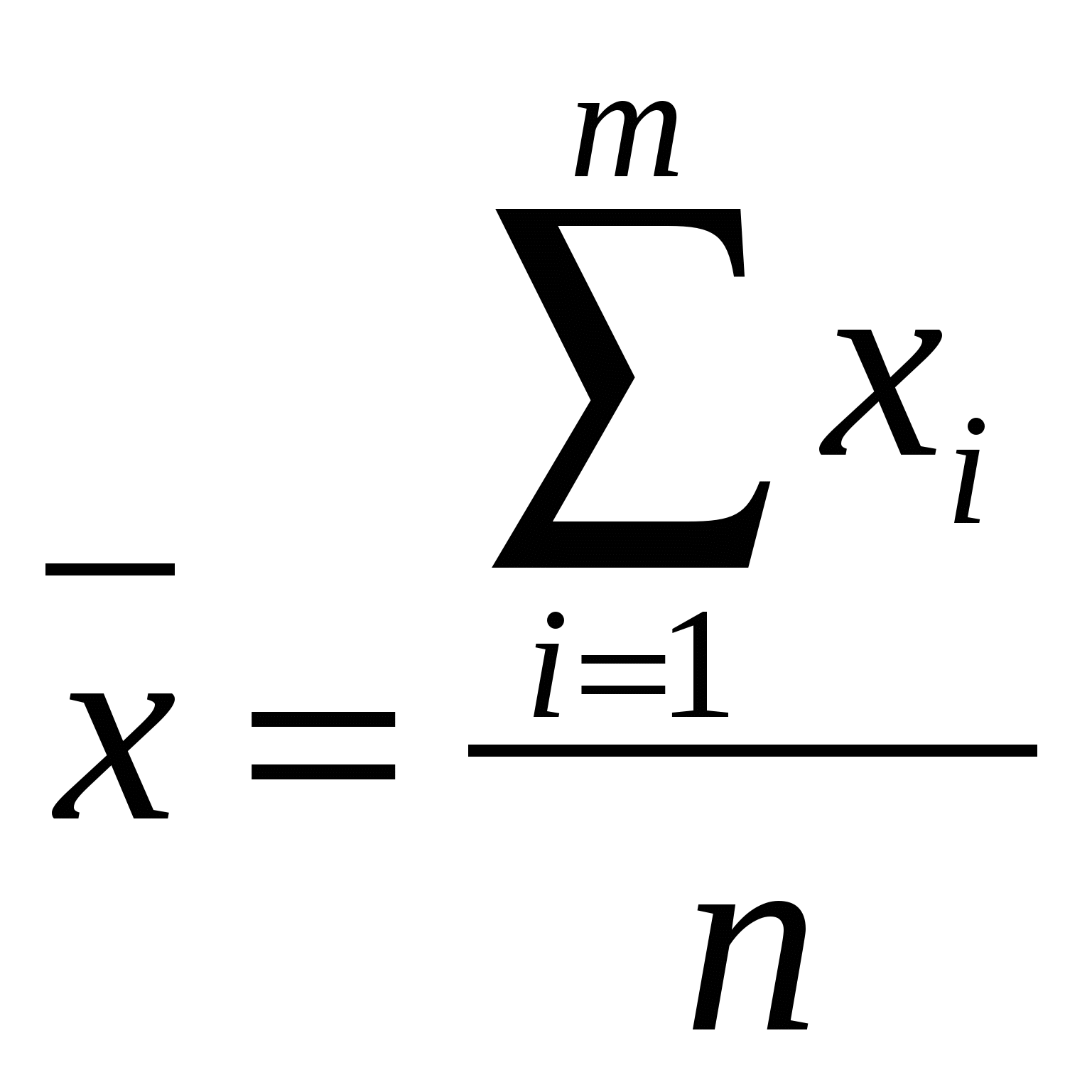)— сумма значений переменной, деленная на n (число значений переменной):

    (1)

    Среднее линейное отклонение (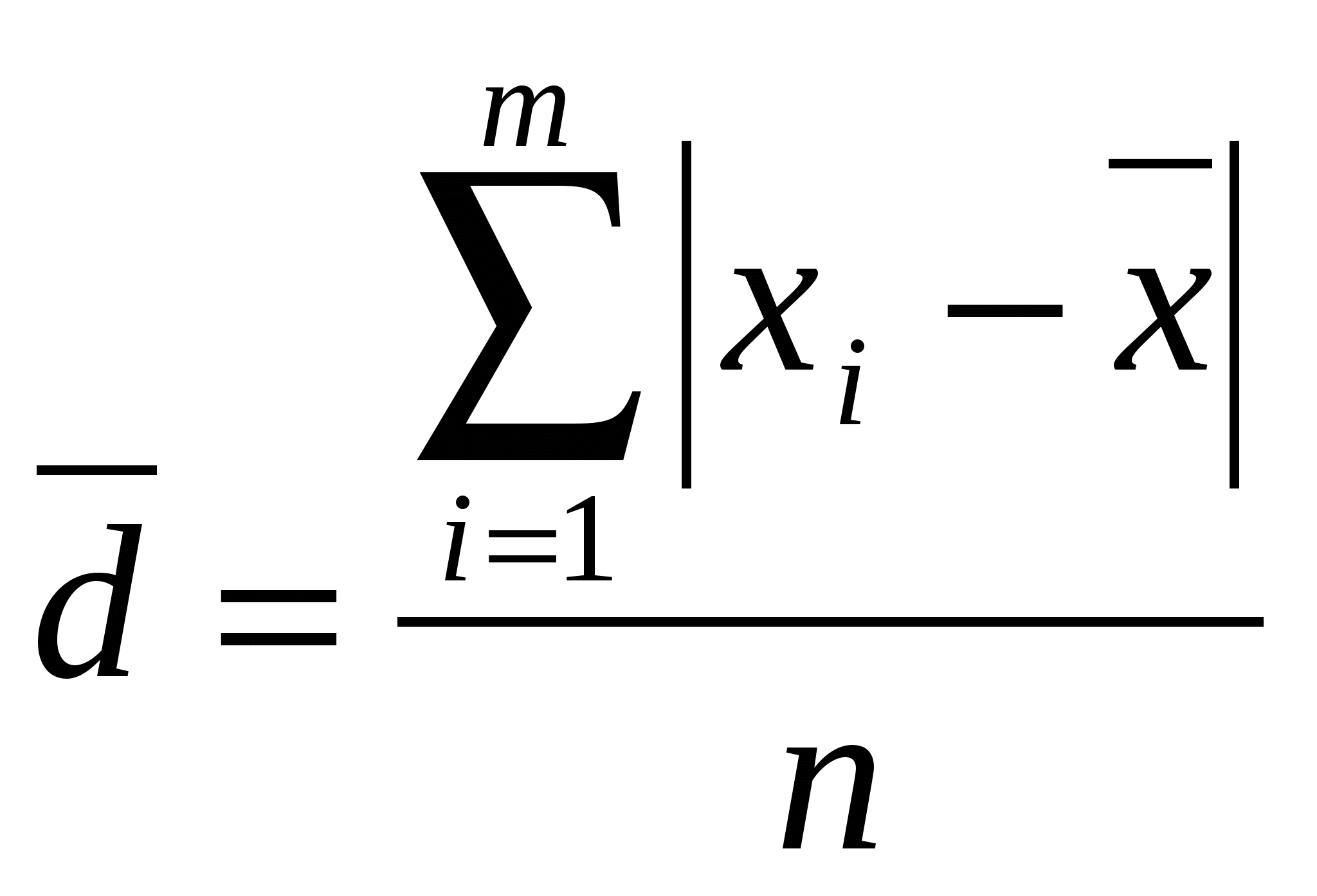) - характеризует меру разброса значений совокупности данных вокруг их среднего значения, определяемое по формуле:

    (2)

    Дисперсия (сигма в квадрате) -представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины. Как и среднее линейное отклонение, дисперсия также отражает меру разброса данных вокруг средней величины.

    Дисперсия бывает двух видов:

    1) простая дисперсия используется для несгруппированных данных и определяется по формуле: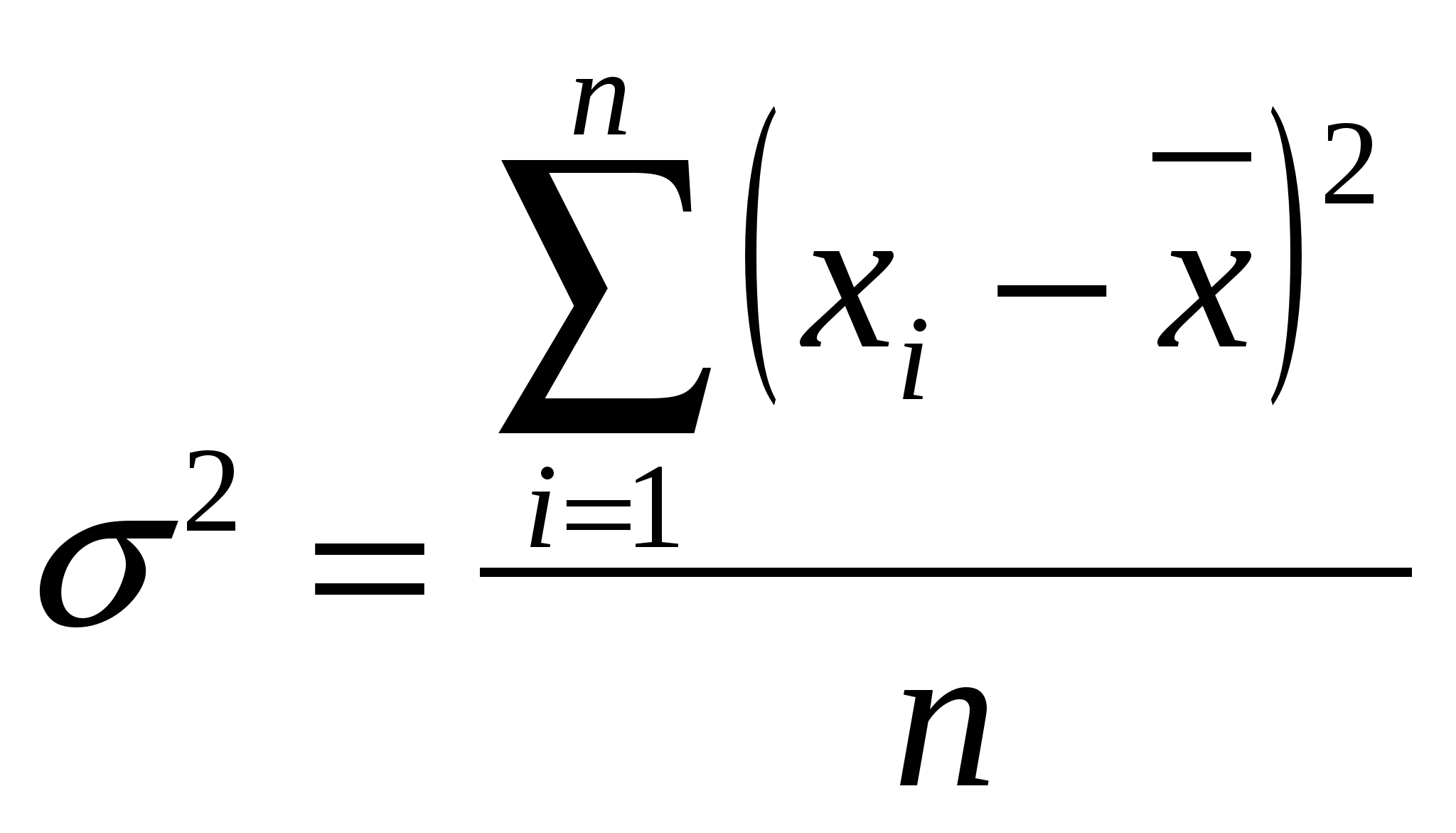

    (3)

    где - i-ое значение переменной;

    - среднее значение переменной;

    - число значений переменной.

    Более удобно вычислять дисперсию по формуле:

    (4)

    которая получается из основной путем несложных преобразований. В этом случае средний квадрат отклонений равен средней из квадратов значений признака минус квадрат средней.

    2) взвешенная дисперсия применяется в случае вариационного ряда и вычисляется по формуле: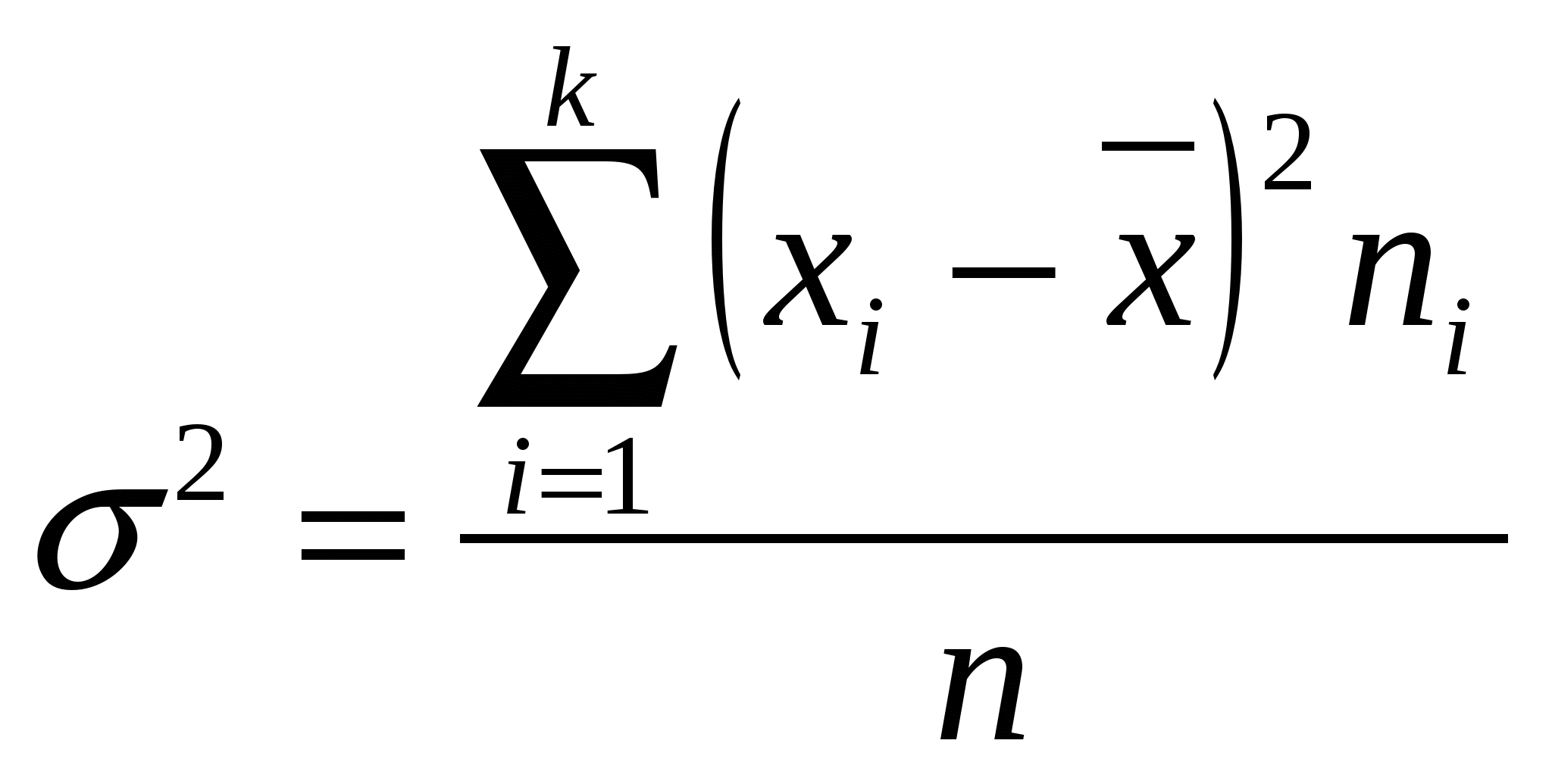

    (5)

    где - i-ое значение переменной;

    - среднее значение переменной

    - частота (повторяемость фактора )

    Дисперсия меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости, когда значения переменной постоянны.

    Чтобы использовать дисперсию дл анализа данных из нее извлекают квадратный корень. Получается так называемое среднеквадратическое отклонение.

    Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего. Часто стандартное отклонение — более удобная характеристика, т.к измерена в тех же единицах, что исходная величина.

    Медиана разбивает выборку на две равные части. Половина значений переменной лежит ниже медианы, половина — выше.

    Медиана дает общее представление о том, где сосредоточены значения переменной, иными словами, где находится ее центр.

    Мода представляет собой максимально часто встречающееся значение переменной (иными словами, наиболее «модное» значение переменной), например, популярная передача на телевидении, модный цвет платья или марка автомобиля и т. д.

    Рассмотрим нахождение основных показателей описательной статистики на примере.

    Задача 1. Имеются данные по группе из 20 студентов. Рассчитать среднее значение, среднее линейное отклонение, построить интервальный ряд распределения, и изучить его дисперсию.

    № п/п
    Рост (см)

    1
    159

    2
    160

    3
    161

    4
    162

    5
    162

    6
    164

    7
    166

    8
    169

    9
    170

    10
    170

    11
    171

    12
    171

    13
    172

    14
    174

    15
    176

    16
    176

    17
    178

    18
    181

    19
    183

    20
    192


    1. По формуле (1) вычисляем среднюю величину роста студентов: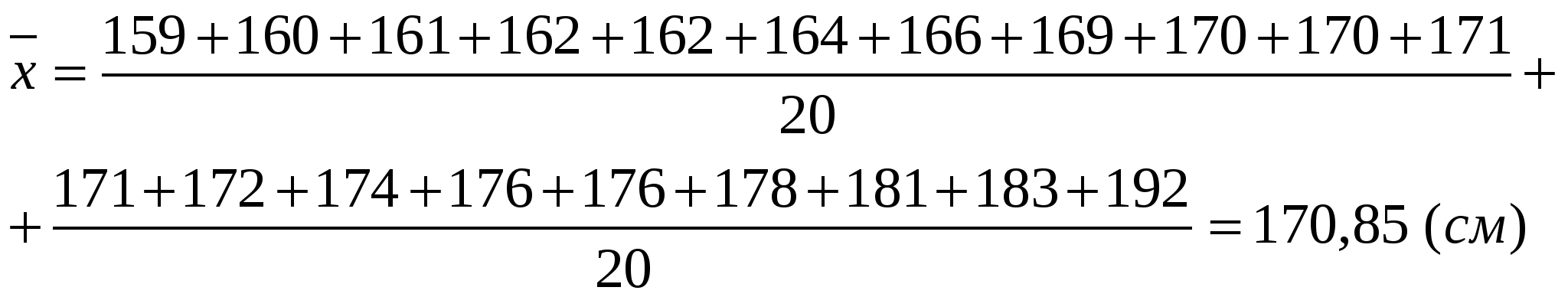



    Вывод: средний рост студентов равен 170,85 см.

    2. По формуле (2) вычисляем среднее линейное отклонение: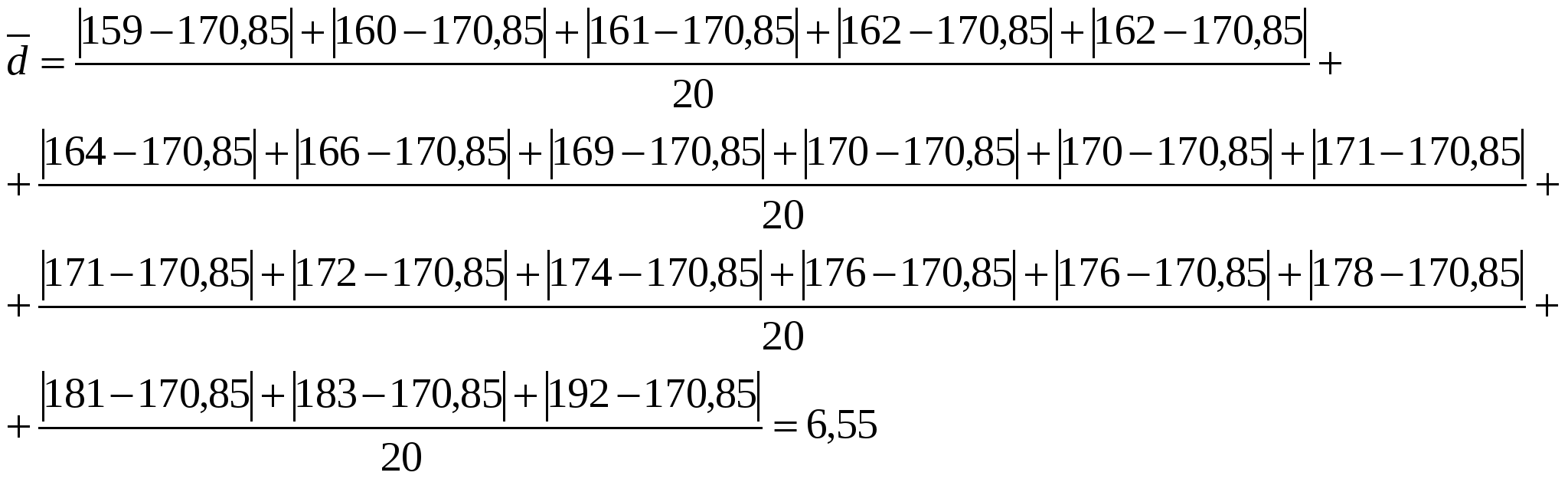



    Вывод: разброс значений совокупности данных вокруг среднего значения, равен 6,55 см.
    3. По формуле (3) найдём значение дисперсию.



    4.Извлекая квадратный корень их дисперсии, находим среднеквадратическое отклонение.

    см.
    Вывод: сравнив полученное значение среднеквадратического отклонения со значением среднего линейного отклонения, рассчитанного в п.2, можно сделать вывод, что среднеквадратическое отклонение является более точным показателем меры рассеяния данных, чем среднее линейное отклонение.
    Построим интервальную группировку.

    1. Определяем количество интервалов по формуле:

    , где N – количество студентов, участвующих в исследовании.

    В нашем случае

    2. Определим шаг интервала по формуле:



    В нашем случае

    3.
    3. Составляем интервальную группировку в виде таблицы.

    Группы студентов по росту
    Число студентов

    159-165,6
    6

    165,6-172,2
    7

    172,2-178,8
    4

    178,8-185,4
    2

    185,4-192
    192

    Сумма
    20


    Для дальнейших расчётов строим вспомогательную таблицу.






































































































    Частота встречаемости ( абсолютная частота ) – число, показывающее, сколько раз объект с данным числовым значением признака встречается в совокупности или ее интервале.

    Абсолютною частоту обозначают символом ni ( µi ).


    Задача №1
    В таблице приведены результаты измерения частоты пульса у 41 некурящих студентов-медиков в возрасте 20 лет:

    Xi
    55
    58
    60
    62
    65
    68
    70

    Pi
    2
    4
    9
    10
    8
    5
    3



    1. Вычислите среднюю величину, стандартное отклонение, моду, медиану, коэффициент вариации (оцените его).

    2. Можно ли считать, что предложенный для анализа признак имеет нормальное распределение?


    Пример. Исследуется случайная величина Х‒ число заболевших гриппом в течение одних суток в некотором городе N.

    Получены данные за первые 150 суток года

    Таблица 1

    3
    5
    4
    4
    5
    8
    2
    3
    1
    6
    6
    1
    2
    5
    5

    4
    4
    4
    3
    4
    5
    5
    2
    2
    3
    4
    3
    2
    4
    4

    8
    10
    1
    4
    3
    3
    2
    5
    7
    5
    3
    6
    7
    5
    6

    1
    4
    6
    4
    5
    4
    5
    7
    6
    5
    3
    5
    5
    8
    7

    7
    5
    5
    4
    5
    3
    3
    6
    3
    5
    2
    2
    2
    6
    2

    5
    6
    8
    4
    4
    8
    3
    6
    4
    4
    5
    5
    7
    5
    5

    3
    5
    4
    5
    5
    4
    7
    6
    9
    3
    5
    5
    6
    6
    3

    4
    5
    2
    6
    7
    5
    5
    4
    2
    5
    2
    2
    6
    2
    7

    5
    5
    8
    5
    3
    5
    2
    5
    3
    7
    6
    6
    3
    6
    0

    4
    4
    4
    5
    2
    7
    7
    3
    1
    1
    6
    6
    5
    7
    6






    написать администратору сайта