билеты. Определение Будем говорить, что во множестве рациональных чисел q произведено сечение, если QАА, а

• Название: Определение Будем говорить, что во множестве рациональных чисел q произведено сечение, если QАА, а
• Анкор: dfghjk
• Дата: 16.10.2021
• Размер: 0.81 Mb.
• Имя файла: билеты.doc
• Тип: Документы; #248827
• страница: 2 из 3

Определение: корня

Пусть существует n>=2

^1/n= ⁿ

множество Е : R : >0 и ⁿ<

множество Е ограничено сверху (оказывается)

^1/n=sup E

Определение: корня с рациональным показателем

Пусть существует r₀=m/n, m,nN, n>=2

Пусть существует R, >0

^r0=(^1/n)^m

Определение: числа в иррациональной степени.

1^=1

Пусть существует >1 и существует R

Множество Е = {^, r<, rQ}

Оказывается, что Е ограничено сверху

^=sup E

Пусть 0<<1

^=1/(1/^

Определение: логарифма

Пусть R, >1, R, >0

Множество Е={xR : ^x<}

Оказывается, что Е ограничено сверху

Log_sup E

Пусть R, 0<<1, >0

Log_- Log_{}

Теорема: Алгебраические операции, которые определены выше обладают всеми теми свойствами, которые известны из школьного курса.

Теория пределов
Определение: Последовательность – числовая функция, определенная на множестве N

{Xn}^oo_n=1 или X_1,X₂, …
Определение: Пусть существует {Xn}^oo_n=1 и существует аR, говорят, что а является пределом последовательности {Xn} или Xn a при n,

Если для >0 существует такой номер N : n>N в.н. |Xn-a|<

или <=> >0 существует N : n>N в.н. |Xn-a|<
Определение: Если а=0, , то последовательность {Xn} называется бесконечно малой (б/м)

Т.о. б/м – это последовательность, взятая целиком, число рассмотренное изолированным не может быть б/м.

Свойства пределов

1. Пусть Xn=a n

Доказательство:

Возьмем >0 N=1 n>1 в.н. |Xn-a|=|a-a|=0<
2. пусть существует {Xn}^oo_n=1a, тогда она ограничена, т.е. Е=
Доказательство:

Возьмем =1, тогда существует N₀ : n> N₀ в.н. |Xn-a|<1 <=> a-1
n=N₀+1, N₀+2, …

Пусть М=max(|X₁|…|X_No|, a+1)

Пусть L=min(-|X₁|…-|X_No|, a-1)
Утверждение: n в.н. L<=Xn
Доказательство: Возьмем n

1. 
   n<=N₀ => Xn<=|Xn|<=max|Xn|<=M
   
2. 
   n>N_0, n=N₀+1 => Xn

3. Существует , С

тогда

Доказательство:

1. 
   Если с=0, y_n=0 для n, тогда
   
2. 
   Если с>0 существует N : n> N в.н. |Xn-a|<с|
   

|y_n-c a|=|c Xn-c a|=|c||Xn-a|<|c|(с|)=


4. , , z_n=x_n+y_n

Тогда
Доказательство:

>0 существует N₁ : n>N₁ в.н. |x_n-a|<

 существует N₂ : n>N₂ в.н. |y_n-b|<

Пусть N=max{N₁,N₂} : n>N в.н. |z_n-a-b|=|x_n-y_n-a-b|=|(x_n-a)+(y_n-b)|<



5. Пусть существует k>=2 функций, которые определены на множестве N

{Xn¹ }^oo_n=1 ; {Xn² }^oo_n=1 ; … {Xn^k }^oo_n=1

Пусть существует С₁,С₂,…,С_k

, l=1,2,…k

Рассмотрим z_n=С₁Xn¹+…+С_kXn^k, тогда



Доказательство:

База: k=2 {Xn¹ }^oo_n=1 ; {Xn² }^oo_n=1




6.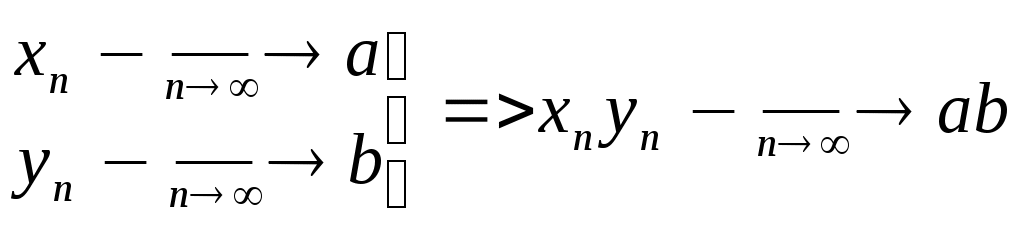

Доказательство:

y_n по свойству 2 она ограничена, т.е. существует k,l : k<=y_n<=l n =>

=> |y_n|<=max(|k|,|l|)

Пусть М=max(|k|,|l|)+1, M>=1, |y_n|<=M

Возьмем >0 и N₁: n>=N₁ в.н. |x_n-a|<

 N₂ : n>N₂ в.н. |y_n-b|<a

max{N₁,N₂}

n>N в.н. (1),(2)

x_ny_n-ab=(x_n-a)y_n +a(y_n-b) => |x_ny_n-ab|<=|(x_n-a)y_n|+|a(y_n-b)|= |x_n-a||y_n|+|a||y_n-b|< a| a


7. Пусть существует {Xn¹ }^oo_n=1 ; {Xn² }^oo_n=1 ; … {Xn^k }^oo_n=1 , k>=2

; ;…; =>



Доказательство:

По методу индукции.

?????
8. x_n0 n , a0 =>

Доказательство:

₀>|a|/2>0 => существует N₀: n>=N₀ в.н. |x_n-a|<|a|

=> (4) |x_n|=|a+(x_n-a)|>=|a|-|x_n-a|>|a|-|a|/2=|a|/2

>0 существует N₁ : n>N₁ в.н. |x_n-a|<(a² 

max(N₁,N₂)= ???

=> (3),(4) выполняется

=
9. x_n0 n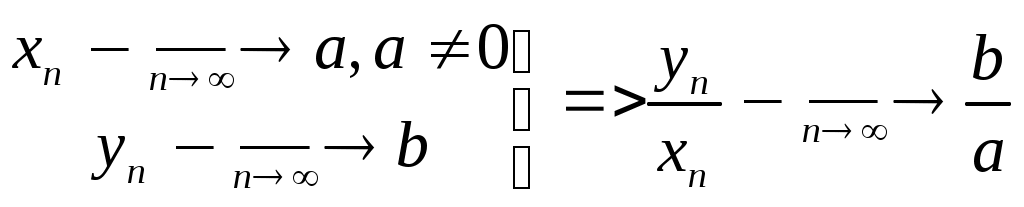



Доказательство: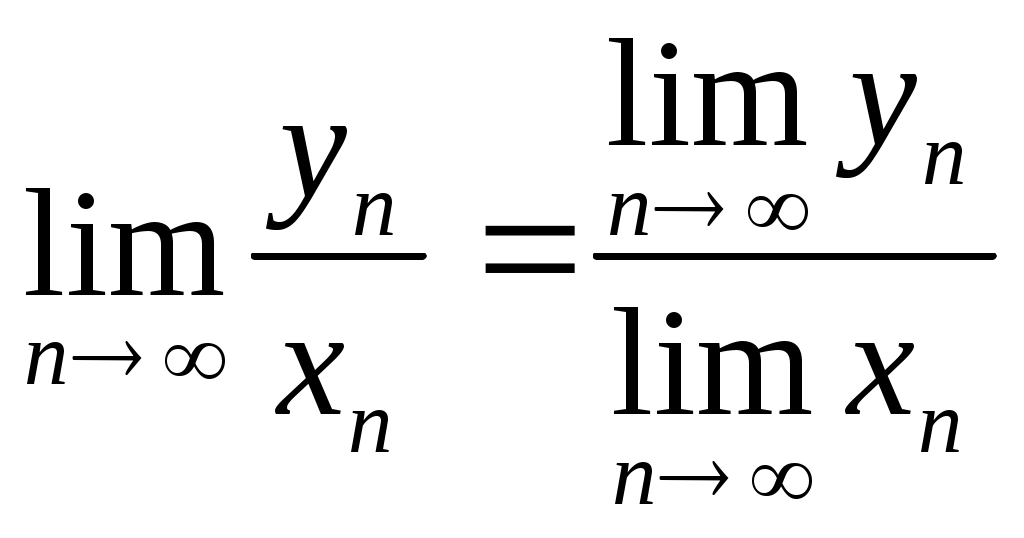

=>
10. => Не существует ba :

(т.е. существует только единственное значение )

Доказательство:

Пусть верно обратное т.е. существует ba : =>

₀>|b-a|/4 => существует N₁ : n>N₁ в.н. |x_n-a|<₀ (5)

 существует N₂ : n>N₂ в.н. |x_n-b|<₀ (6)

Пусть N=N₁+ N₂+1 для x_n выполняется (5),(6)

an=a+(x_n-a)<=a+|x_n-a|
x_n=b+(x_n-b)>=b-|x_n-b|>b-(b-a)/4>(a+b)/2 (8)

по (7) и (8) Значит наше предположение неверно, т.е. существует только единственное значение
Предельный переход в неравенствах

Теорема: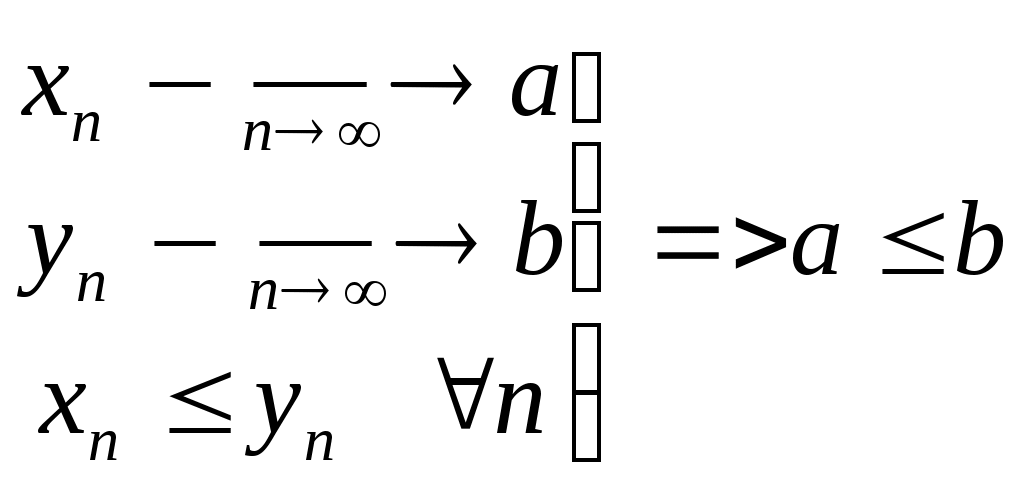



Доказательство:

 существует N₁ : n>N₁ в.н. |x_n-a|< (9)

 существует N₂ : n>N₂ в.н. |y_n-b|</2 (10)

n₀=N₁+ N₂+1, n₀>N₁, n₀>N₂

(9) <=> a-_n
(10) <=> b-<y_n(10`)

a-n<=y_n
Если бы a>b, тогда (a-b)/2

11. 
    => a a

Значит наше предположение неверно, т.е. a<=b
Теорема: о трех последовательностях

x_n,y_n,z_n

, , x_n<=y_n<=z_n n =>

>0 существует N₁ : n>N₁ в.н. |x_n-a|< (12)

 существует N₂ : n>N₂ в.н. |z_n-a|< (13)

N=max(N₁,N₂) n>N => (12),(13) выполняется

( 12) <=> a-_n a-n<=y_n<=z_n
(13) <=> a-<z_n(13`)

=> a-n |y_n-a|< т.е.

Предел монотонной последовательности

Определение:

Последовательность {x_n}^oo_n=1 называется монотонно возрастающей или просто возрастающей, если n выполняется неравенство x_n<=x_n+1

Последовательность {y_n}^oo_n=1 называется монотонно убывающей или просто убывающей, если n выполняется неравенство y_n>=y_n+1

Последовательность {z_n}^oo_n=1 называется монотонной, если она возрастает или убывает.

Последовательность {x_n}^oo_n=1 называется строго возрастающей, если n выполняется неравенство x_nn+1

Последовательность {y_n}^oo_n=1 называется строго убывающей, если n выполняется неравенство y_n>y_n+1

Последовательность называется строго монотонной если она либо строго возрастает, либо строго убывает.
Теорема:

а) {x_n}^oo_n=1 возрастает и ограничена сверху и существует k : n выполняется неравенство x_n

б) {y_n}^oo_n=1 убывает и ограничена снизу и существует h : n выполняется неравенство y_n>h, тогда существует b :

Доказательство: а)

1) Рассмотрим множество всех значений, которые принимает последовательность, как функция определенная на множестве N

E= (1) (множество ограничено сверху)

Существует sup E=a, aR
Лемма:

Пусть а – число, определенное в (1), тогда а=

Доказательство:

Возьмем >0 : n в.н. x_n<=sup E=a
Покажем (a-). Эта величина не является точной границей, значит существует N : x_N >a- n>N
x_N<=x_N+1<=…<=x_n-1<=x_n => x_N<=x_n

a-< x_N<=x_n => a-n< a+ <=> |x_n-a|<

т.е.
Доказательство: б)

1) Пусть существует y_n>=y_n+1 {y_n}^oo_n=1

Пусть L : y_n>=L n

Пусть x_n – вспомогательная последовательность : -y_n=x_n, тогда

-y_n<=-y_n+1 n => x_n<= x_n+1 т.е. {x_n} возрастает

2) y_n>=L ; -y_n<=-L ; -L=k

имеет x_n<=k n значит по пункту а) существует а :

3) –a=b

y_n=-x_n =(-1) X_n, тогда по свойству 3


Дополнение:

1. 
   Пусть {x_n}^oo_n=1 возрастает и ограничена сверху т.е. x_n<=k
   

Пусть а= , тогда x_n<=а n

Если {x_n} строго возрастает, то x_n<а n

2. 
   Пусть {y_n}^oo_n=1 убывает и ограничена снизу т.е. y_n>=L
   

Пусть b= , тогда y_n>=b n

Если {x_n} строго убывает, то y_n>b n
Доказательство:

(1) x_n<= x_n+1<=a => x_n
т.е. а=sup E

x_n
x_n<=a
Доказательство (2) аналогично
Число e

Названо в честь Eiler

0,1,e – важные числа в математике
Две специальные последовательности

, nN

, nN

Теорема: Последовательность {x_n}^oo_n=1 строго возрастает

{y_n}^oo_n=1 строго убывает

=> {x_n} и {y_n} имеют общий предел

Существует =e e=2,718281828459045

Существует =e (за е обозначим общий предел)

Доказательство:

Пусть установлено, что {x_n} строго возрастает, а {y_n} строго убывает,

т.е. y_n>x_n

x₁<…n-1nnn-1<…1

т.е. x₁nnn-1 => x_n1 n

y_n>x₁ n

Если последовательность монотонная то {x_n} ограничена сверху, а {y_n} ограничена снизу.

По теореме о существовании предела монотонной последовательности:

Существует =е₁, существует =e₂ (3)

<=> е₁



e₂ = e₁

1   2   3