билеты. Определение Будем говорить, что во множестве рациональных чисел q произведено сечение, если QАА, а

• Название: Определение Будем говорить, что во множестве рациональных чисел q произведено сечение, если QАА, а
• Анкор: dfghjk
• Дата: 16.10.2021
• Размер: 0.81 Mb.
• Имя файла: билеты.doc
• Тип: Документы; #248827
• страница: 3 из 3

^. 1 =e

Если {x_n} строго возрастает и {y_n} строго убывает, то они имеют общий предел е.

Проверка монотонности последовательностей {x_n}, {y_n}

a,b

, n>=2

Рассмотрим при а=1

??? (4)

Следствие из (4)

b>0 => (1+b)ⁿ >=1+C ¹_nb



(1+b)ⁿ >=1+n b
Убывание последовательности y_n

Рассмотрим y_n-1/ y_n ,n>=2

y_n строго убывает <=> y_n-1/ y_n>1

Доказательство: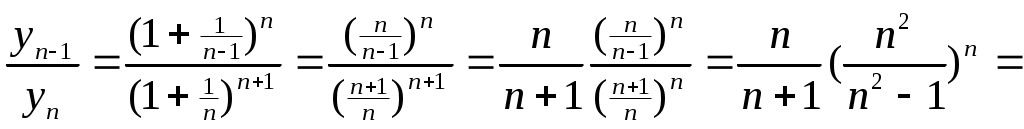





Строгое возрастание х_n





Пусть b=1/n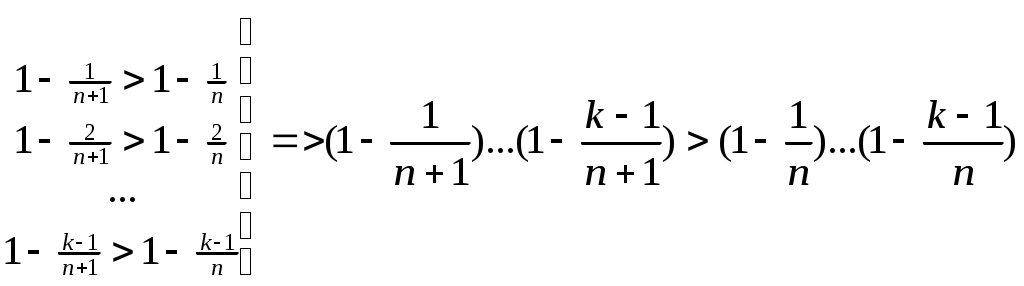



(1)




(2)

(3)

(4)

(3),(4) =>
(5)

Учитывая теорему о существовании числа е и дополнение к теореме о пределе монотонной последовательности получаем:

n>=1 (1+1/n)ⁿn+1 (6) NB

x_nn
Формула числа е

Теорема

по свойству 8


Бесконечные пределы последовательностей

<=> A>0 существует N : n>N в.н. x_n>A

<=> B<0 существует N : n>N в.н. y_n
Свойства:

1 ) =>

=>

2) C>0

C<0

3. 
   =>
   

y_n ограничена
z_n=(-1)ⁿ n не существует
Бесконечно большие и бесконечно малые последовательности
Определение:

Последовательность {x_n} является бесконечно малой (б/м) <=>

Последовательность {y_n} является бесконечно большой (б/б) в узком смысле <=>

Последовательность {y_n} является бесконечно большой (б/б) в широком смысле <=>

Последовательность z_n=(-1)ⁿ n является бесконечно большой (б/б) в широком смысле, т.к.

Теорема:

Пусть y_n0 и является б/б в широком смысле, тогда x_n=1/ y_n является б/м.

Пусть w_n0 и является б/м, тогда z_n=1/ w_n является б/б в широком смысле

Если w_n состоит из чисел одного знака, то z_n является б/б в узком смысле
Предел функции в точке
Определение: Пусть существует функция f определенная на (a,b)\{x₀} (x₀(a,b))

( ) <=> >0 существует >0 : x(a,b)\{x₀} : |x-x₀|< в.н. |f(x)-A|<
Определение: Пусть существует функция g определенная на (a,b)\{x₀} (x₀(a,b))

( ) <=> L>0 существует >0 : x(a,b)\{x₀} : |x-x₀|< в.н. g(x)>L
Определение: Пусть существует функция h определенная на (a,b)\{x₀} (x₀(a,b))

( ) <=> k>0 существует >0 : x(a,b)\{x₀} : |x-x₀|< в.н. h(x)Определение: Пусть существует функция f определенная на (a,b)

( ) <=> >0 существует >0 : x(a,b) : aОпределение: Пусть существует функция f определенная на (a,b)

( ) <=> >0 существует >0 : x(a,b) : b-Определение: Пусть существует функция g определенная на (a,b)

( ) <=> L>0 существует >0 : x(a,b) : aL
Определение: Пусть существует функция h определенная на (a,b)

( ) <=> k>0 существует >0 : x(a,b) : aОпределение: Пусть существует функция g определенная на (a,b)

( ) <=> L>0 существует >0 : x(a,b) : b-L
Определение: Пусть существует функция h определенная на (a,b)

( ) <=> k>0 существует >0 : x(a,b) : b-Предел справа или слева, конечный или бесконечный называется односторонним пределом функции.

??????

Свойства предела функции
Для пределов функции (конечных) справедливы свойства соответственно свойствам [1-10]\{2} для пределов последовательности.

Свойство 2 справедливо, но оно требует индивидуальной формулировки.
Покажем эквивалентность свойств «3» =а+0

3. ;

Доказательство всех свойств пределов функции проводится аналогично доказательству свойств пределов последовательности.

?????
Некоторые существенные неравенства
1) nN

e>1

1. 
   =>
   

0=2 :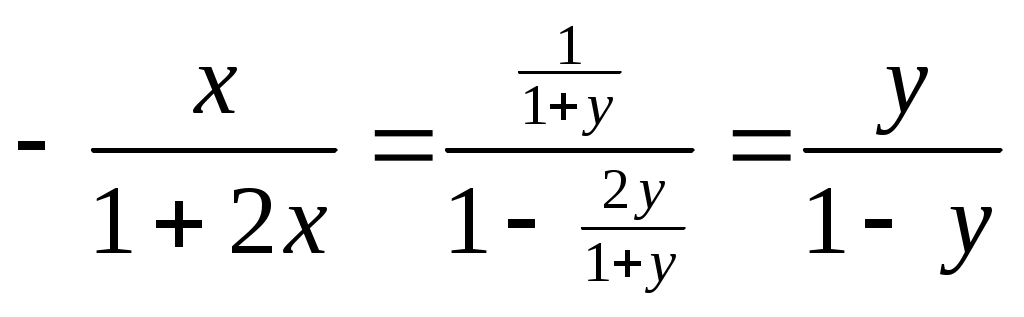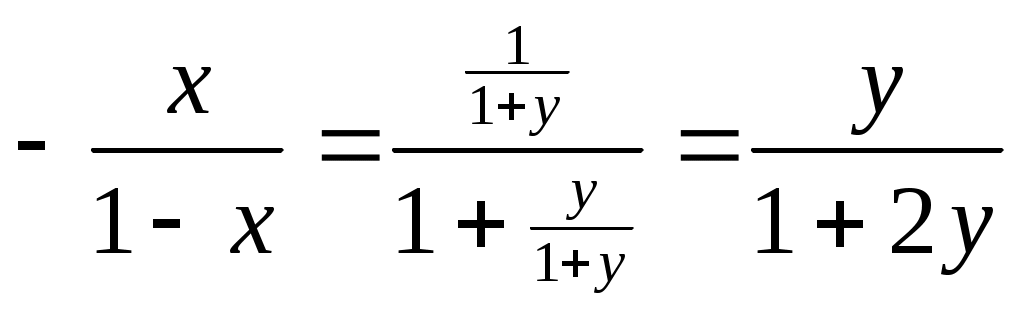

0 (4)

-1/3<=y<0







;

(6); -1/3<=y<0

(4), (6) => 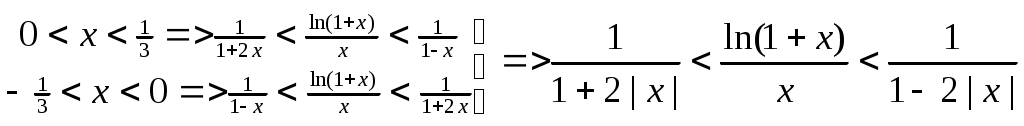x0 |x|<=1/3

, x0 |x|<=1/3
nN =>

=>

0

n>=3.

Подставим получим:

Пусть существует у : -1/3<=y<0 x=-y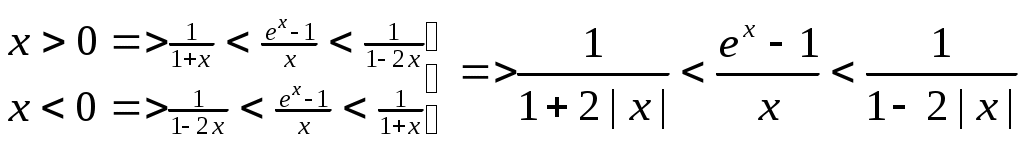





при x0 |x|<=1/3



, x0 |x|<=1/3





0<|x|<1 => Cos x=Cos |x| =



(1)



,

(2)


-1/3<=x<0







-1/3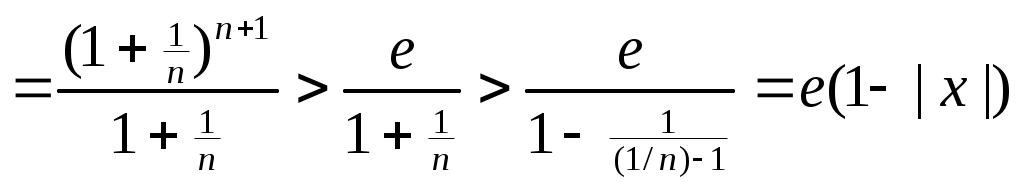<=x<0





-1/3<=x<0 (4)

0<|x|<=1/3 (5)

Ослабление (3), (4)


Замечательные пределы
Пусть существуют f,g,h определенные на (a,b)\{x₀} (x₀(a,b))

x f(x)<=g(x)<=h(x)

| =>

|

1. 
   
   

Доказательство:

Рассмотрим существенное неравенство (5)

; ;

=> =>

=> => =>

2. 
   
   

|x|<0, x0 => 1-|x|
; ;

=>

=>

3. 
   
   

; ;

=>

=> =>

4. 
   
   

; ;

=>

=> =>
Лемма:

f(x) определена на (-а,а)\{0}

f(x)0 x0

=>

Существует >0 : x0 |x|< |f(x)|<1/3

U=f(x)



=> =>

5. 
   , r0
   

Доказательство:





Определение:

Пусть существует f определенная на (a,b) (x₀(a,b)), тогда

Существует предел

Если функция g определена на [a,b), то говорят, g непрерывна в точке а или существует

Если функция g не непрерывна в точке а, то говорят, что она разрывна в точке а.

Пусть h определена на (a,b], то говорят, что h непрерывна в точке b, если существует
Арифметические свойства непрерывных функций в точке
Пусть  - любое значение

1. 
   Пусть f непрерывна в точке , тогда Сf непрерывна в точке .
   
2. 
   Пусть f,g непрерывны в точке , тогда f+g непрерывна в точке .
   
3. 
   Пусть f,g непрерывны в точке , тогда fg непрерывна в точке .
   
4. 
   Пусть f(x)0 x и f непрерывна в точке , тогда 1/f непрерывна в точке .
   
5. 
   Пусть f(x)0 x и f,g непрерывны в точке , тогда g/f непрерывна в точке .
   

Доказательство: (5)

b (a,b], f,g непрерывны в точке b.

f(x)0 x

Пусть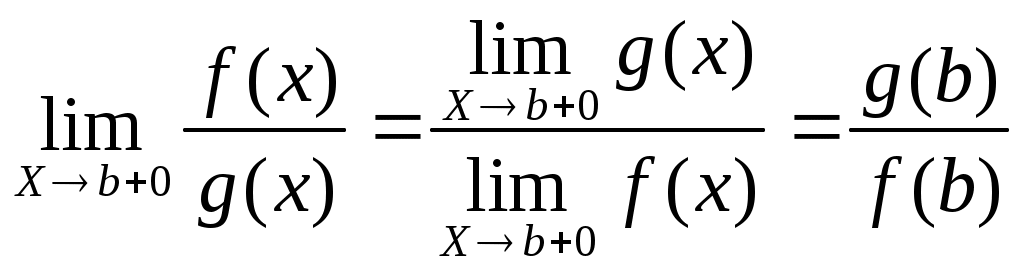



Остальные аналогично
Теорема:

П усть f[a,b], g[a,b], f непрерывна в точке , f()=

P<=f(x)<=q x[a,b]

Пусть g(y) определена на [p,q] и непрерывна в точке , => h(x) непр.

h(x)=g(f(x))

Лемма:

Пусть f(x) непрерывна в точке  <=>

<=>>0 существует >0 : x[a,b] : |x-|< в.н. |f(x)-f(|<

т.к. (1) верно для x=, то мы можем не накладывать ???

>0, существует >0 : y[p,q] : |y-|< в.н. |g(y)-g(|<

>0 существует >0 : [a,b] : |x-|< в.н. |f(x)-f(|<3

Пусть |h(x)-h(|-|g(f(x))-g(f(|=|g(y)-g(|<<=>|y-|<
I

По существенному неравенству (4) для ln(x) |x|<=1/3 x0



1+x=t 2/3<=t<=4/3







=>

ln(x) непрерывна в точке х=1

Пусть x₀>0 ln(x)=ln(x₀)+ln(x/x₀)

=> ln(x) непрерывная функция.
II

x=0

при x0 |x|<=1/3





=>



x₀ ,

,
III

x=0



IV

Sin x
0<|x₁|</2

|Sin x₁|=Sin |x₁|<|x₁|



|x|</2

x₀0 x=(x-x₀)+x₀

Sin x=Sin x₀ Cos(x-x₀)+ Cos x₀ Sin(x-x₀)

Cos x=Cos x₀ Cos(x-x₀)+ Sin x₀ Sin(x-x₀)

Отсутствие непрерывности – разрыв

Ликвидация разрыва
x(a,b), f

Существует

f не является непрерывной в точке x₀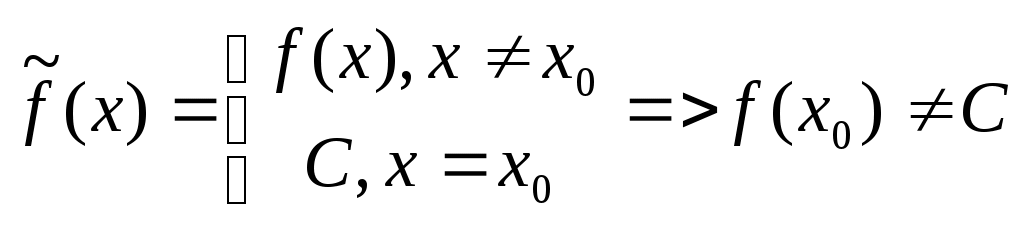





x₀(a,b)

g, pq

Существует

Существует
Свойства функций, непрерывных на замкнутом промежутке
Определение: f определена на [a,b], a<=x<=b, говорят, что функция непрерывна на [a,b], если она непрерывна в любой точке на [a,b]
Теорема: Больцана-Коши

f(a) ^. f(b)<0, тогда существует x₀(a,b) : f(x₀)=0

Доказательство:

g(a)=m

g(b)=n

mn

f(x)=g(x)-r

f(a)=m-r

f(b)=n-r

f(a) ^. f(b)=(m-r)(n-r)<0

Пусть x₁(a,b), f(x₁)=0 <=> g(x₁)=r
Теорема: о непрерывности обратной функции.

Пусть f(x) непрерывна на a,b] и строго монотонна на нем, тогда на (a,b), определена и непрерывна функция обратная данной, причем если f(x) возрастала, то f(x)^-1 тоже возрастает, если f(x) убывала, то f(x)^-1 тоже убывает.

Пусть m=min(f(a),f(b)), n=max(f(a),f(b)).

???
Теорема: о элементарных функциях.

Любая элементарная функция непрерывна в любом промежутке, в котором она определена.
Теорема: Вейерштрасса 1.

Существует M,m : m<=f(x)<=M, пусть f(x) непрерывна на [a,b]
???
Теорема: Вейерштрасса 2.

Пусть f(x) непрерывна на [a,b], тогда существует x₁,x₂(a,b) : f(x₁)<=f(x)<=f(x₂) (4)

Доказательство:

Пусть М – Sup{f(x)} x[a,b]

(3) => M<+oo f(x₂)=M

Пусть f(x)=M – не существует f(x)
(x)=1/(M-f(x))>0

Существует L>0 (x)<=L x (5)

(5) <=> M-f(x)>=1/L <=> f(x)<=M-1/L

Существует x₂ : f(x)<=f(x₂) x

g(x)=-f(x)

Существует x₁ : g(x)<=g(x₁) <=> f(x)>=f(x₁)

Производные и ее основные свойства
Определение Пусть существует f определенная на (a,b), пусть x₀(a,b), тогда говорят, что функция f имеет производную в точке x₀, если существует (1)

Говорят, что функция дифференцируема в точке х₀ , если существует такая постоянная величина А и некая (h) при h0, для которых справедливо свойство:

f(x₀+h)-f(x₀)=Ah+(h) (2) и (3)
Теорема: Функция f имеет производную в точке х₀, тогда и только тогда, когда она дифференцируема в точке х₀. При это для значения f `(x<sub>0</sub>) и для числа А справедливо равенство А= f `(x₀)

Замечание: Из определения производной функции в силу свойства единственности предела, следует, что если существует производная в точке х₀, то она единственна. Определение не гарантирует, что существует единственное А.
Применение этой теоремы влечет единственность А
Доказательство: теоремы

Пусть существует производная

1. 
   => (5)
   
2. 
   <=> f(x₀+h)-f(x₀)= f `(x₀)+hr(h)
   

A=f `(x₀)



(5)=>(3)
Пусть функция дифференцируема

=>f `(x₀)=A
Арифметические свойства функции, имеющей производную

1. 
   f определена на (a,b), x₀(a,b), тогда f непрерывна на (а,b)
   

Доказательство:

f(x₀+h)-f(x₀)=Аh+(h) <=> f(x₀+h)=f(x₀)+Аh+(h)

f(x₀) = f(x₀) +0 + 0 (h0)

Значит f непрерывна на (а,b)

2. 
   Пусть существует f `(x₀), C, тогда
   

(Cf)`(x<sub>0</sub>)=C f `(x₀)

Доказательство:

по свойствам предела

3. 
   Пусть существует f `(x<sub>0</sub>), g `(x₀), тогда (f­+g)`(x<sub>0</sub>)=f `(x₀)+g `(x₀)
   

Доказательство:

4. 
   Пусть существует f `(x<sub>0</sub>), g `(x₀), тогда (fg)`(x<sub>0</sub>)=f `(x₀) g(x₀)+g `(x₀) f(x₀)
   

Доказательство: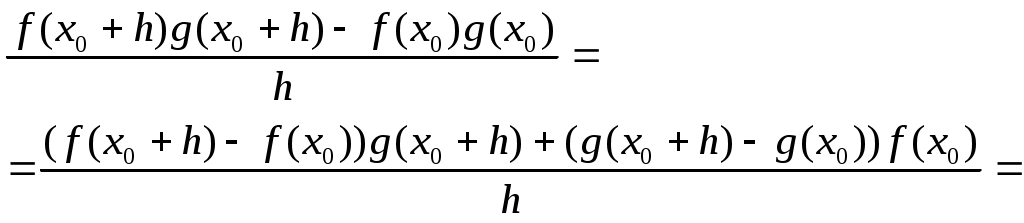



= f `(x<sub>0</sub>) g(x<sub>0</sub>)+g `(x₀) f(x₀)

5. 
   Пусть существует g `(x₀) : g(x₀)0 x(a,b), тогда
   

Доказательство: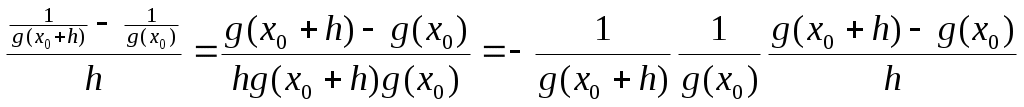

6. 
   Пусть существует f `(x<sub>0</sub>), g `(x₀) : g(x₀)0 x(a,b), тогда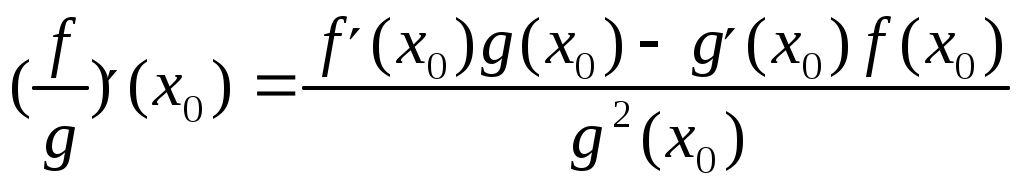
   

Доказательство:

7. 
   Производная сложной функции
   

f определена на (a,b) : p0=f(x₀) существует g`(y₀)

(x₀)=g(f(x₀))

`(x<sub>0</sub>)=g`(y₀)f `(x₀)

Доказательство:

По определению и равенства (8)

(8)=>H=f(x₀+h)-f(x₀)=f `(x₀)h+₂(h) (9)

=> g`(y<sub>0</sub>) (f `(x₀)h+₂(h))+₁(f `(x₀)h+₂(h)

?????????????????

8. 
   Производная обратной функции.
   

Пусть f определена, непрерывна и строго монотонна на [a,b]

Пусть x₀(a,b)

Пусть f дифференцируема в точке x₀, существует f `(x₀)0

g(y) – обратная функция, у₀=f(x₀)

Тогда g дифференцируема в точке y₀ и g`(y<sub>0</sub>)=1/f `(x₀)

Доказательство:

f(x₀+h)-f(x₀)=f `(x₀)h+(h)



f(x₀+h)=y₀+l

g(f(x₀+h))=g(y₀+l), x₀+h=g(y₀+l)

f(x₀)= у₀

g(f(x₀))=g(y₀)

x₀= g(y₀)

h= g(y₀+l)-g(y₀)

y₀+l-y₀=f `(x₀)(g(y₀+l)-g(y₀))+(g(y₀+l)-g(y₀))

(1)=> g(y₀+l)-g(y₀)=1/ f `(x<sub>0</sub>)<sup>.</sup>l +((-1/ f `(x₀))(g(y₀+l)-g(y₀)))

₁(l)= (1/ f `(x₀))(g(y₀+l)-g(y₀))

g(y₀+l)-g(y₀)=(1/ f `(x₀))₁(l)


Таблица основных производных

1) С`=0 Доказательство:



2) x`=1 Доказательство:



2`) (ax+b)`=1 Доказательство: (ax+b)`=ax`+b`=a

3) (x²)`=(x x)`=x` x+x x`=2x

(xⁿ)`=nx^n-1 ; xⁿ⁺¹=xⁿ x

3`)x0 (x<sup>-n</sup>)`=1/xⁿ= -nx^-n-1

4) (e^x)`= e^x Доказательство:



4`) (e<sup>Cx</sup>)`= C e^Cx Доказательство: (e^Cx)`= (e<sup>y</sup> )` (Cx)` (y=Cx)

5) (ln x)`=1/x , x>0 Доказательство:

y=ln x <=> x=e^y

(ln x)`=1/e^y=1/x (Обратная функция)

6. 
   r0 rR, x>0 (x^r)`=r x^r-1 Доказательство:
   

(r ln x)`=r (ln x)`=r/x

(x^r)=(e^{r ln x})`= (e^{r ln x})(r/x)= r x^r-1

7. 
   (Sin x)`=Cos x
   

(Cos x)`=-Sin x

Доказательство:

Пусть x=0,



Sin x= Sin (x-x₀+x₀)=Sin x₀ Cos(x-x₀)+ Cos x₀ Sin(x-x₀)

Cos x=Cos(x-x₀+x₀)=Cos x₀ Cos(x-x₀)-Sin x₀ Sin(x-x₀)

(Sin x)`=Sin x<sub>0</sub>(Cos(y))`(x-x₀)`+ Cos x<sub>0</sub>(Sin(y))`(x-x₀)`= Sin x₀ 1 0+Cos x₀ 1 1= =Cos x₀ (x=x₀)

Cos x аналогично

8. 
   (tg x)`=1/cos²x
   

(ctg x)`=-1/sin²x

(tg x)`=

9. 
   (arcsin(x))`=
   

(arccos(x))`=

Доказательство:

y=arcsin(x), x=sin(y) -/2
(arcsin(x))`=1/(sin(y))`=1/cos(y)=

10) (arctg(x))`=

(arcctg(x))`=–

y=arctg(y), x=tg(y) -/2
(arctg(x))`=1/(tg(y))`=cos²(y)

x=tg y => x²+1= tg²y+1= sin²(y)/cos²(y)+1=1/cos²(y)


Теорема Ферма

Определение:

f определена на [a,b], x₀(a,b)

говорят, что функция является точкой локального максимума, если существует >0 : x(x₀-,x₀+) в.н. f(x)<=f(x₀)

g определена на [a,b], x₀(a,b)

говорят, что функция является точкой локального минимума, если существует >0 : x(x₀-,x₀+) в.н. g(x)>=g(x₀)

h определена на [a,b], x₀(a,b)

говорят, что функция является точкой локального экстремума, если x₀ является точкой локального минимума или точкой локального максимума.

Замечание: Если в точке х₀ функция f достигает своего min или max значения на (a,b), то она имеет на нем локальный экстремум.
Теорема: Пусть f определена на [a,b] х₀(a,b).

Пусть f имеет производную в точке х₀ и пусть существует экстремум, тогда f `(х₀)=0

Доказательство:

Пусть существует >0 : 00)<=f(х₀) => (2)

(2) =>

h<0 => (3)

3. 
   =>
   

По теореме об одностороннем пределе т.е. f `(x₀)=0
Теорема Ролля

f(a)=f(b)

f определена на [a,b] и непрерывна на нем и дифференцируема в любой точке.

Существует х₀(a,b) f `(х₀)=0 (Существует f(x) x(a,b))
Доказательство:

Рассмотрим 2 случая

1. 
   Пусть f=const, тогда f `(x)=0 m=M
   
2. 
   Т.к. f(a)=f(b), тогда либо mf(a)=f(b), либо Mf(a)=f(b), либо M,mf(a)=f(b), тогда m или M достигают ???????
   

Теорема Лагранжа

Пусть f определена и непрерывна на [a,b] существуют f `(x) х[a,b], тогда f(b)-f(a)=f `(x₀)(b-a), x₀(a,b).

Доказательство: L= (f(b)-f(a))/a

(x)= f(x)-f(a)-L(x-a)

 определена и непрерывна на [a,b]

существует `(x) х(a,b)

(а)=0 |

(b)=0 | => существует х₀ : `(x₀)=0 (по теореме Ролля)

Теорема Коши

f,g определена и непрерывна на [a,b]

g`(x)0 х

g(a)g(b) и существует x₀(a,b) :

Доказательство:

1)g(b)-g(a)=g`(x)

2)

(x)=f(x)-f(a)-k(g(x)-g(a))

`(x)=f `(x)-kg`(x)

(a)=0

(b)=0

f `(x<sub>0</sub>)-kg`(x₀)=0

f `(x<sub>0</sub>)=kg`(x₀)