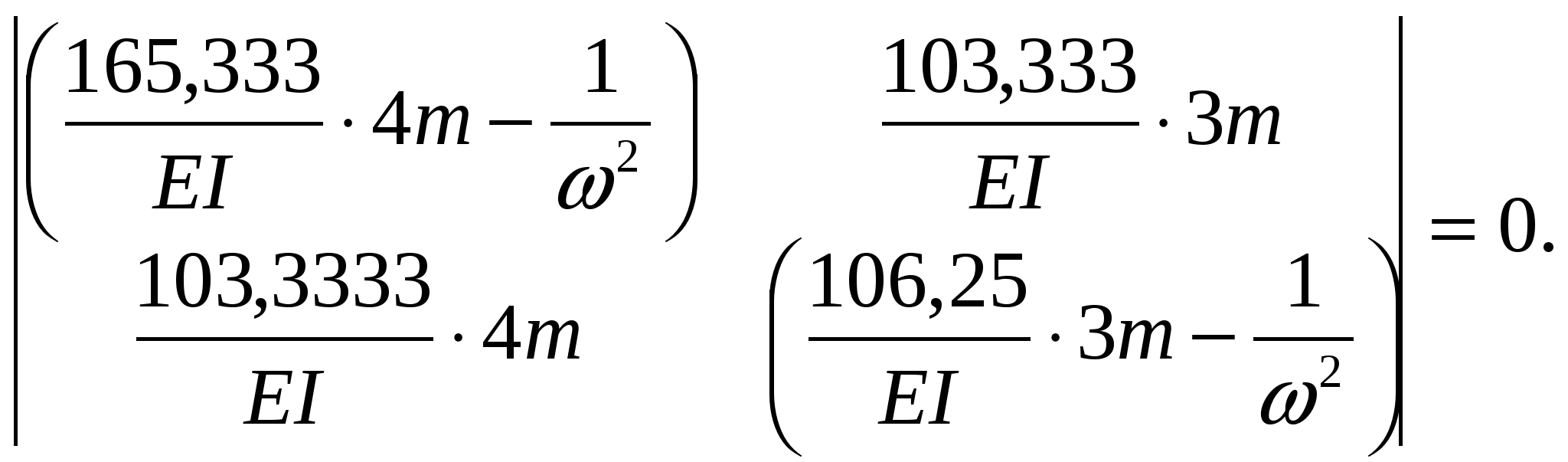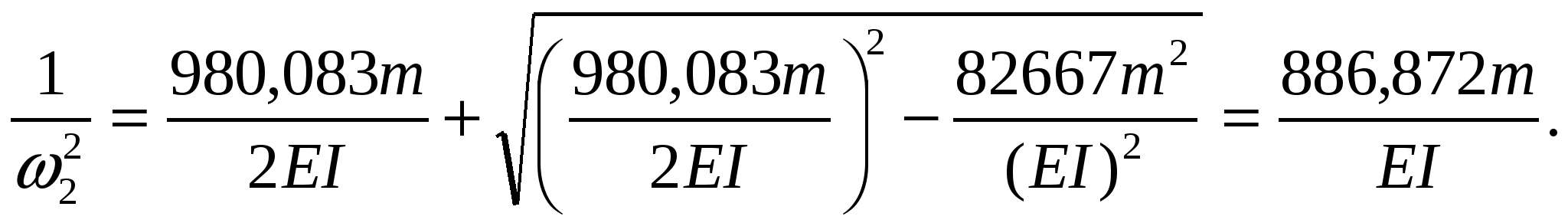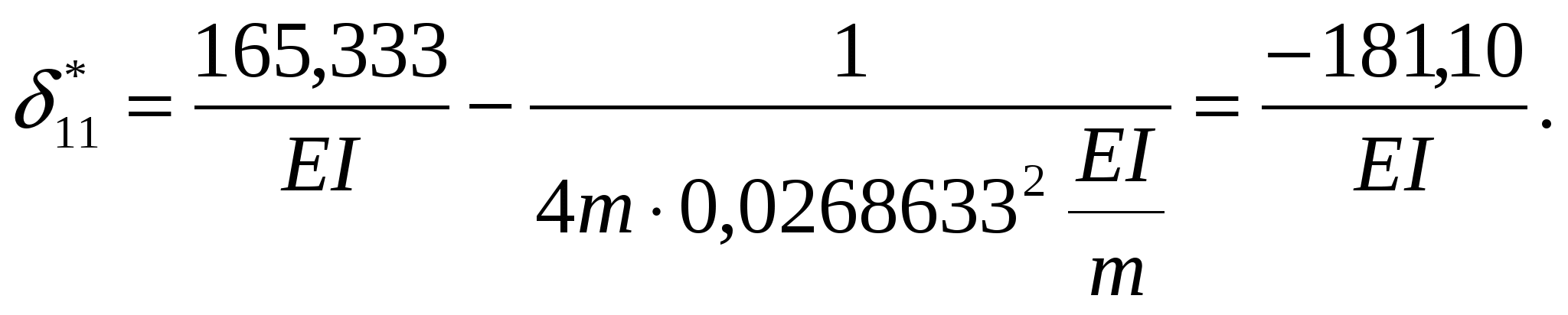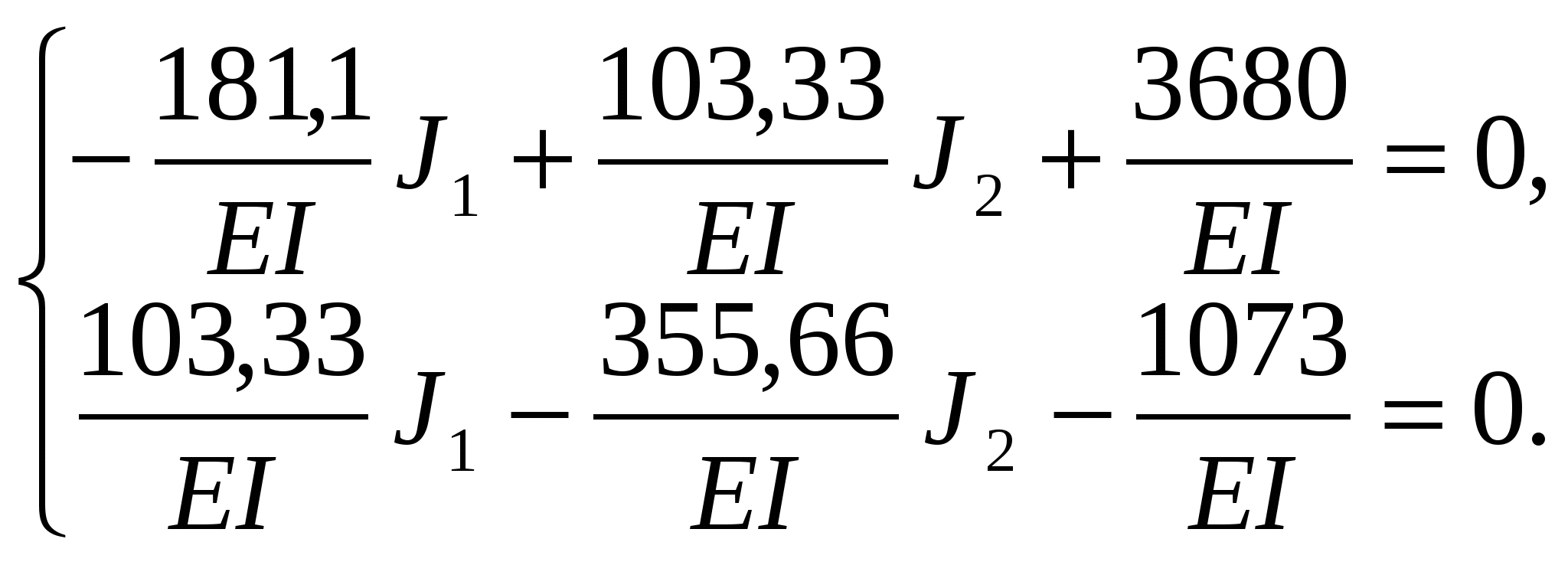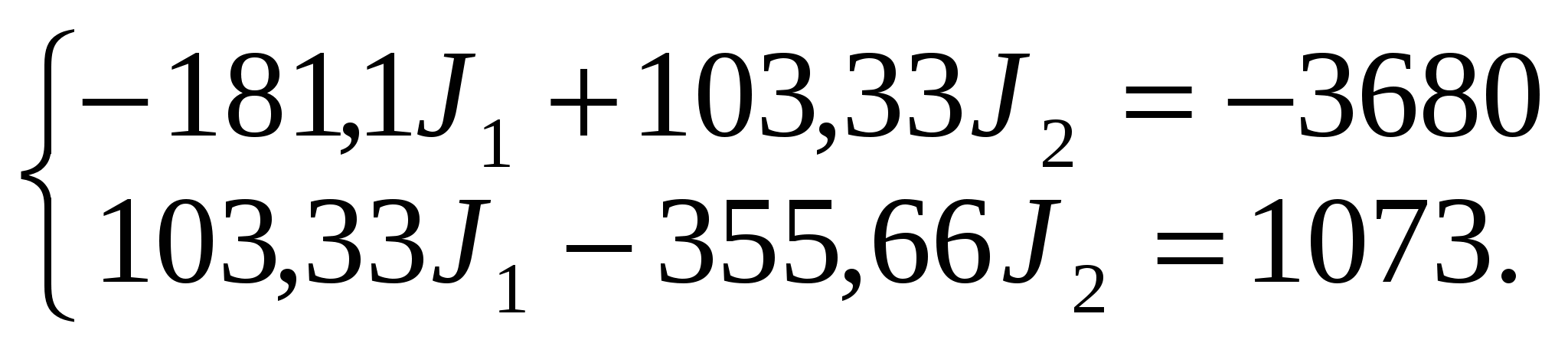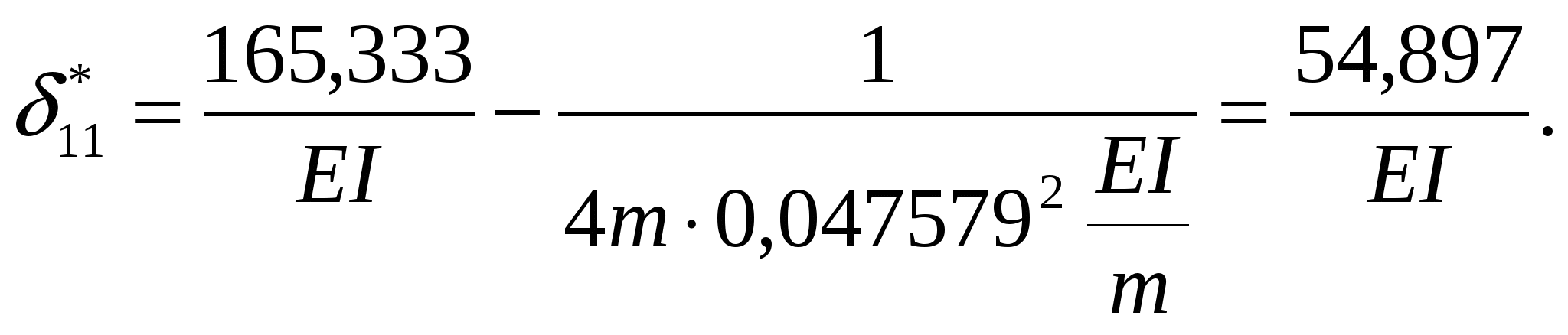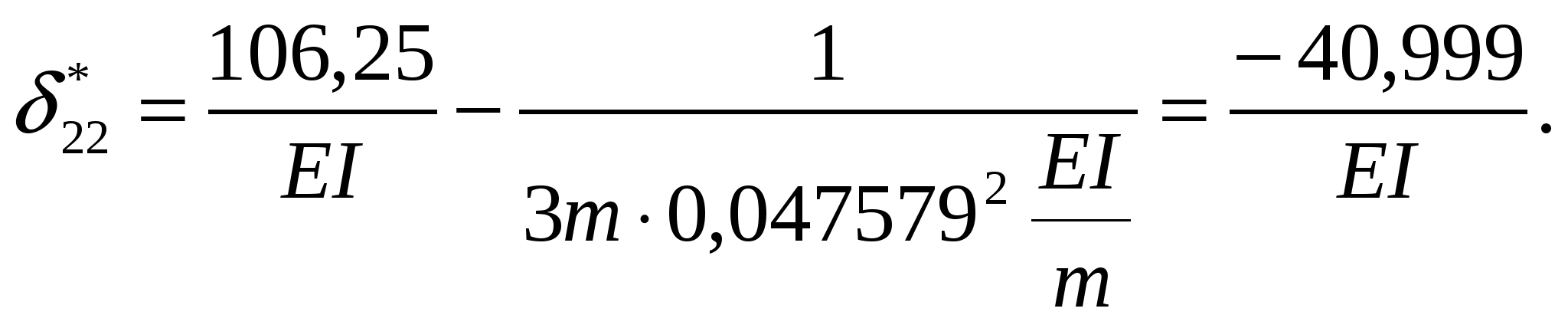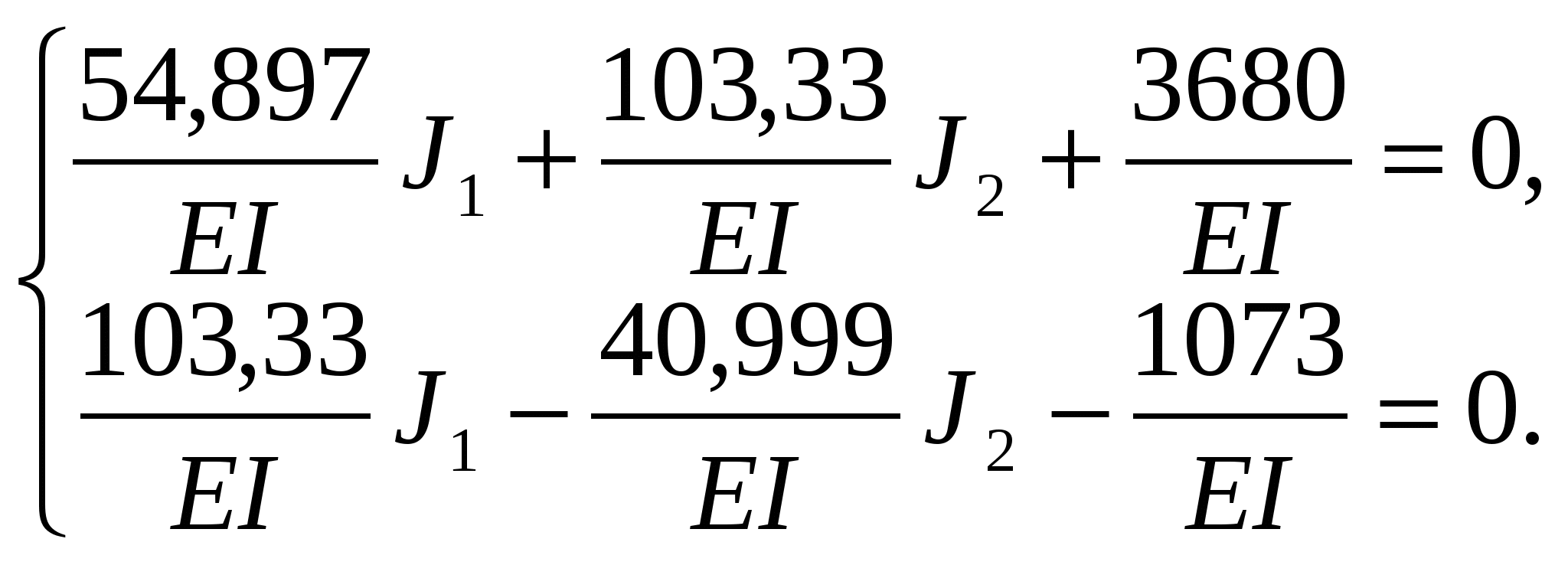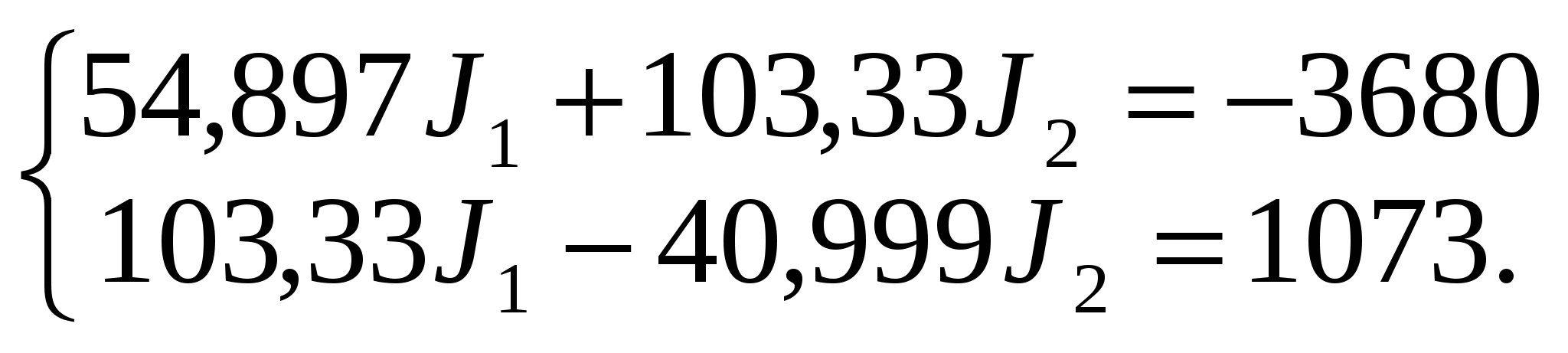|
ЗАДАНИЕ 1
ОПРЕДЕЛЕНИЕ ЧАСТОТ И ФОРМ СОБСТВЕННЫХ
КОЛЕБАНИЙ РАМ С СОСРЕДОТОЧЕННЫМИ МАССАМИ
Для заданного варианта № 68 (рис. 1) при геометрических размерах и нагрузке по строке 24 таблицы требуется:
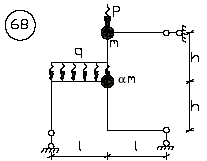
Рис. 1
Таблица
Номер строки
|
l, м
|
h, м
|
|
P, кН
|
q, кН/м
|
24
|
8
|
5
|
3
|
20
|
0,5
|
1. Составить частотное уравнение;
2. Определить спектр частот собственных колебаний;
3. Найти формы собственных колебаний:
4. Проверить ортогональность найденных форм собственных колебаний аналитическим методом.
Решение
Система имеет две сосредоточенные массы (рис. 2). Нижняя масса 3m может совершать колебания как по вертикали, так и по горизонтали. Верхняя масса m может совершать только вертикальные колебания, так как горизонтальному перемещению мешает шарнирная подвижная опора. Рама имеет две динамические степени свободы потому, что обе массы по вертикали могут перемещаться только вместе.
На рис. 3 показаны инерционные силы. Первая инерционная вертикальная сила возникает от колебания верхней и нижней массы, поэтому m1 = m+ 3m = 4m. Вторая горизонтальная инерционная сила приложена только к нижней массе, поэтому m2 = 3m.

Рис. 2

Рис. 3
Вычислим опорные реакции при действии единичной инерционной силы J1 = 1.
Из уравнения ΣX= 0: XC = 0;
ΣMA= YB16 – 18 = 0. YB = 0,5.
ΣY = YB + YA + 1 = 0. YA = 1 – YB = 1 – 0,5 = 0,5.
Опорные реакции получились положительными. Это означает, что выбранные направления совпадают с их действительными направлениями.
Вычислим опорные реакции при действии единичной инерционной силы J2 = 1.
Из уравнения ΣX= 0: 1 - XC = 0; XC = 1.
ΣMC= YА16 –15 = 0. YA = 5/16 = 0,3125.
ΣY = 0: YA – YB = 0; YB = YA = 5/16 = 0,3125.
Опорные реакции получились положительными. Это означает, что выбранные направления совпадают с их действительными направлениями.
Построим эпюры изгибающих моментов от единичных сил инерции (рис. 4 и 5).

Рис. 4
Для вычисления перемещения 11 умножаем эпюру М1 саму на себя:
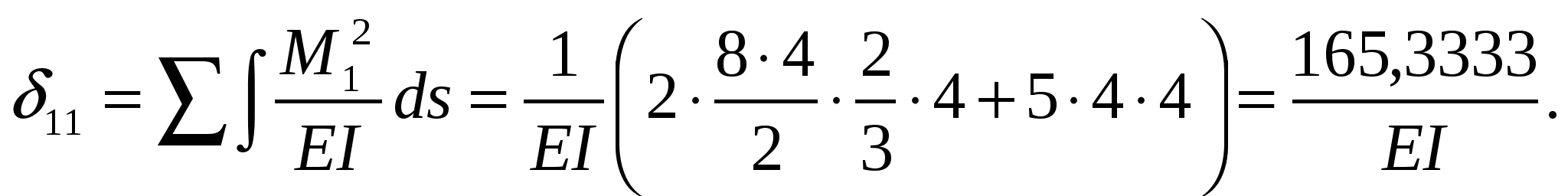
Для вычисления перемещения 22 умножаем эпюру М2 саму на себя:
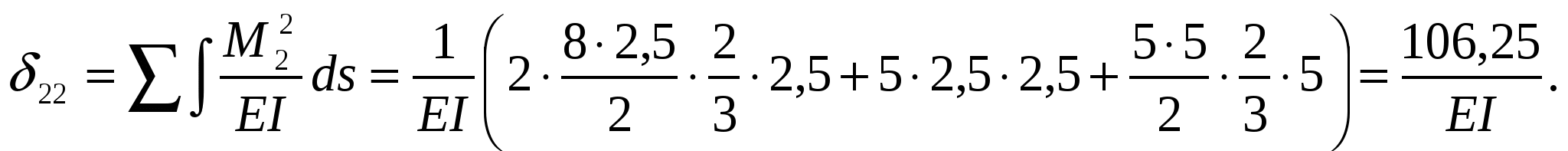
Для вычисления перемещения 12 умножаем эпюру М2 на М1:
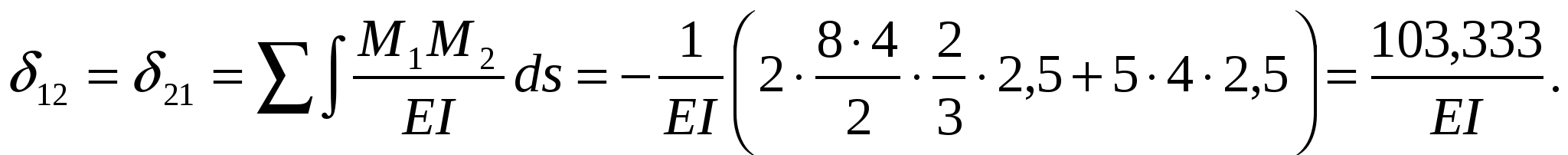

Рис. 5
Частоты свободных колебаний определяются из частотного уравнения (это уравнение также называют характеристическим и вековым), которое можно записать с помощью определителя следующим образом:

Подставив значения перемещений и масс, получим
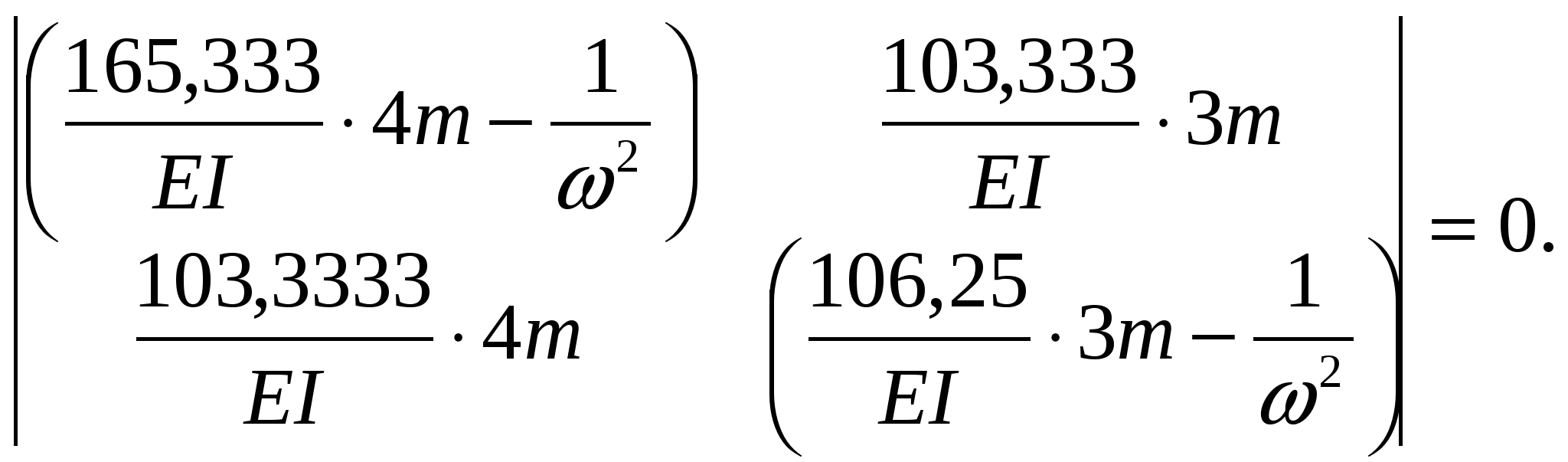
Раскрыв определитель, получим частотное уравнение в виде алгебраического уравнения второй степени относительно 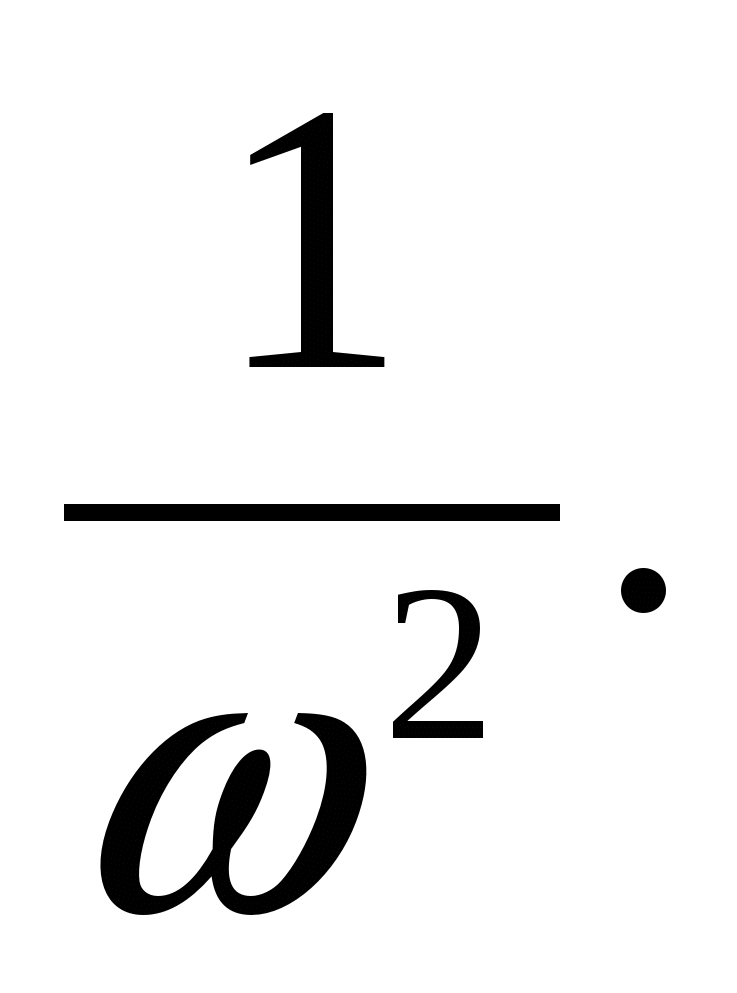
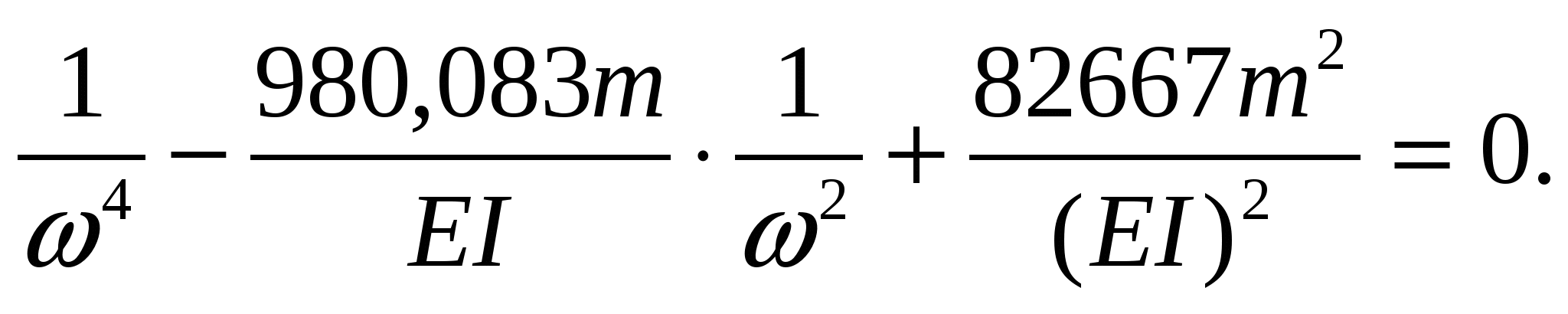
Два корня этого уравнения будут положительными и не равными нулю.
 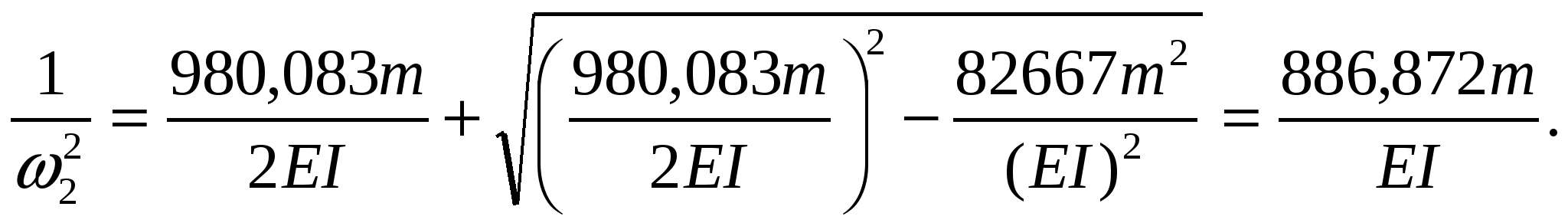
Отсюда частоты собственных колебаний будут равны:

Для проверки найденных частот определим формы колебания. Для этого подставляем найденные частоты собственных колебаний в уравнение
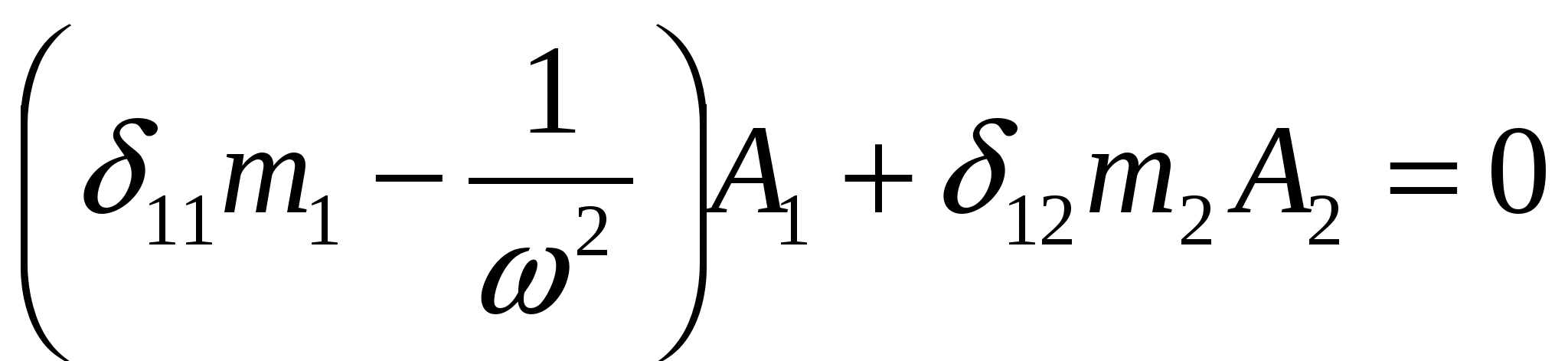 . .
Для первой частоты 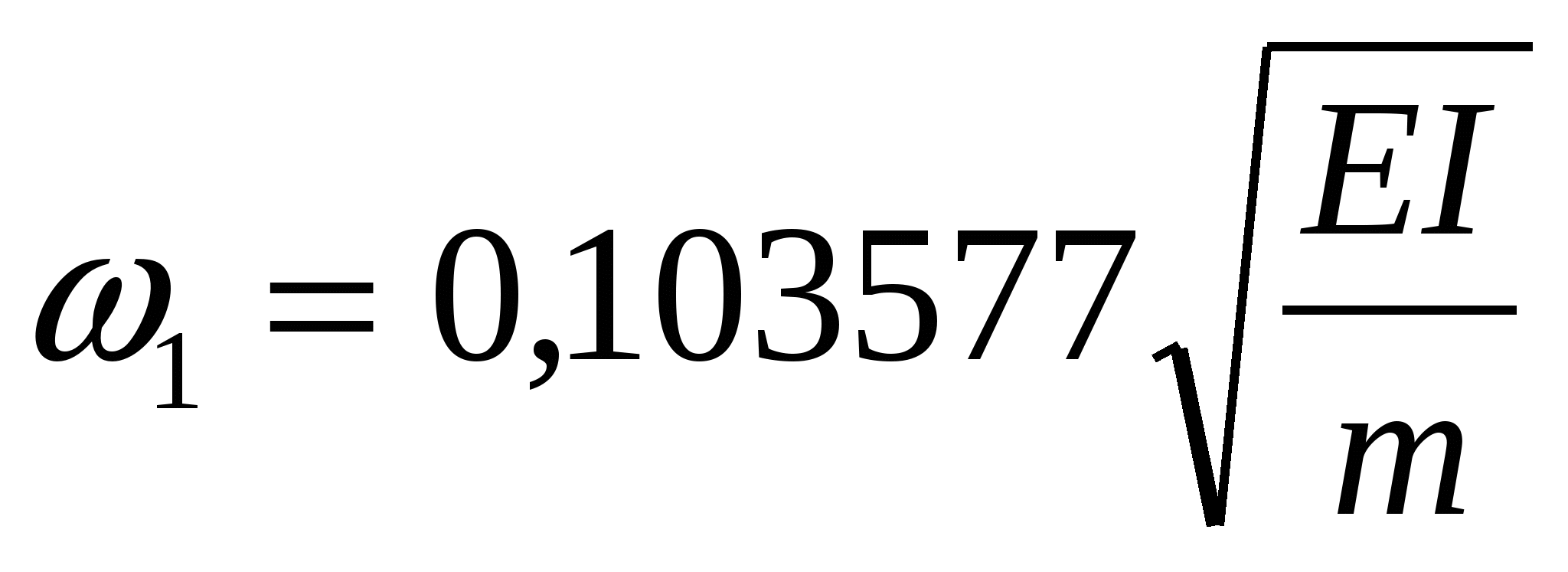 получим получим

Приравняв вторую амплитуду к единице, 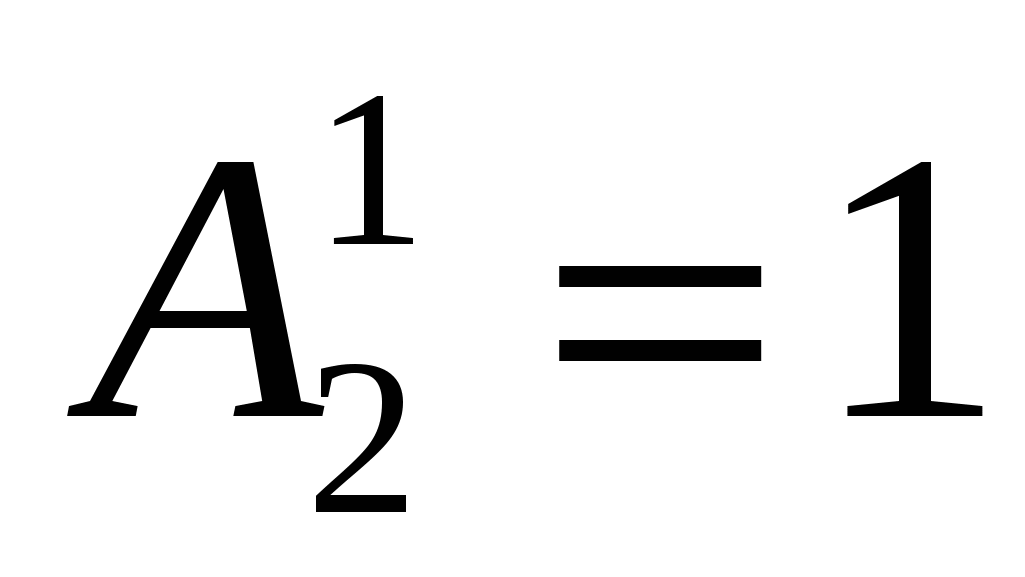 , тогда первая амплитуда из уравнения будет равна , тогда первая амплитуда из уравнения будет равна
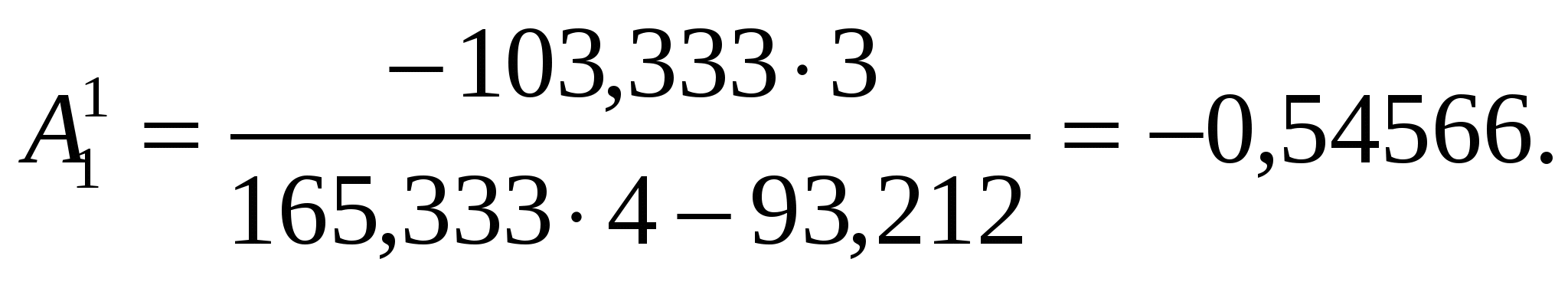
Для второй частоты  получим получим
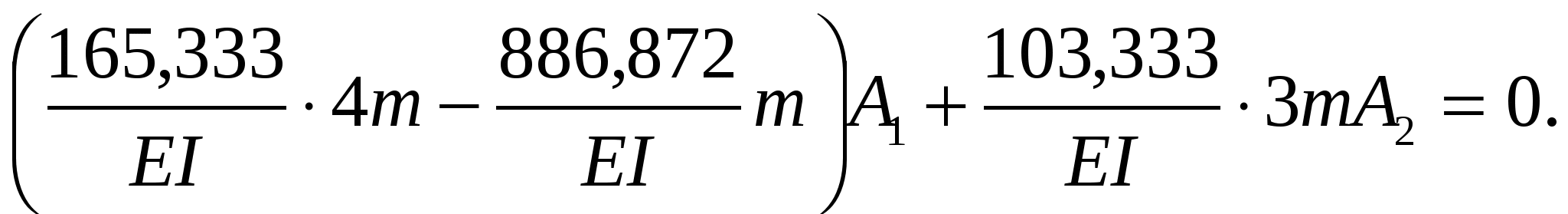
Приравняв вторую амплитуду к единице,  , тогда первая амплитуда из уравнения будет равна , тогда первая амплитуда из уравнения будет равна

Проверим ортогональность форм колебаний, подставив найденные амплитуды в уравнение 
4m(-0,54566)1,3745 + 3m11 = -0,000039 0.
ЗАДАНИЕ 2 ДИНАМИЧЕСКИЙ РАСЧЕТ РАМ С СОСРЕДОТОЧЕННЫМИ МАССАМИ НА ВИБРАЦИОННУЮ НАГРУЗКУ
1. Для рамы из задания 8 построить эпюры динамических усилий M, Q, N (амплитудные значения) при двух частотах возмущающей нагрузки:
1 = 0,8min; 2 = min + 0,2(2 – min).
2. Определить динамические перемещения масс.
Примечание:
1. В таблице даны амплитудные значения динамических нагрузок:
P(t) = Psint; q(t) = qsint.
2. Жесткость всех стержней EI = const.
Решение
В предыдущем задании для данной рамы определены частоты собственных колебаний
 . .
Вычисляем частоту вынуждающей нагрузки:

Перемещения ij были определены ранее.
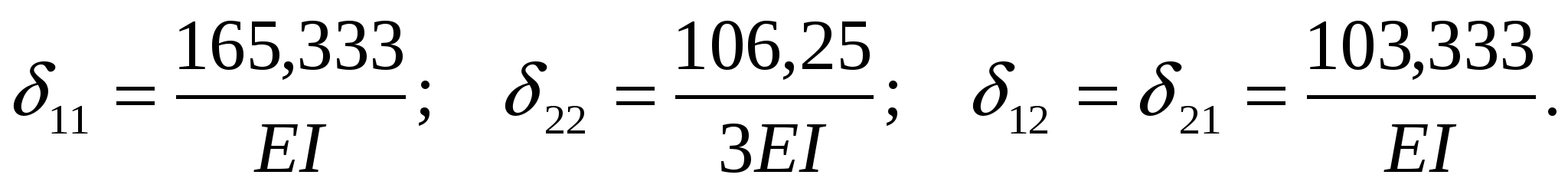
Найдем значения *ii.
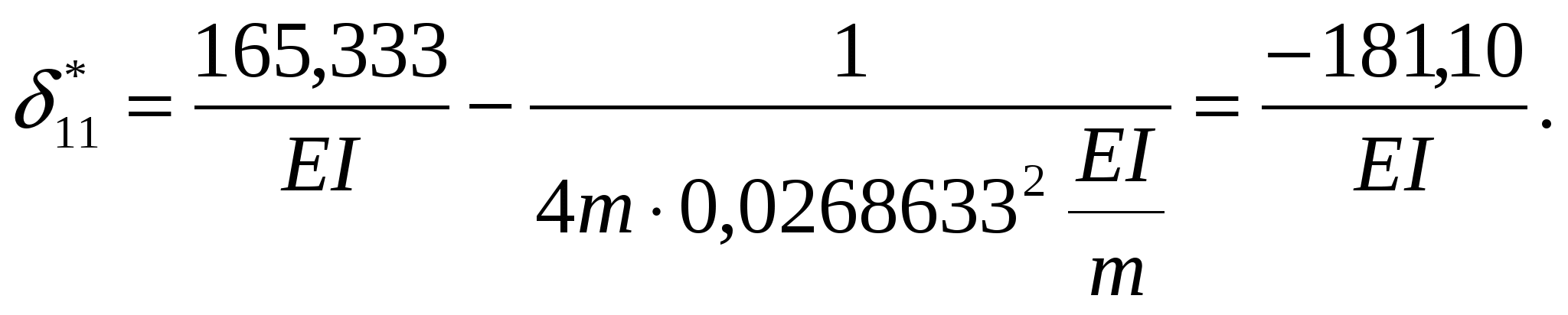

Вычислим опорные реакции при действии динамической нагрузки (рис. 6).
Из уравнения ΣX= 0: XC = 0;
ΣMС= YА16 – q8(4+8) - P8 = 0.
YA = 0,75 q8 + 0,5P = 0,750,58 + 0,520 = 13 кН.
ΣY = YB + YA – q8 – P = 0. YB = q8 + P – YA = 0,58 + 20 – 13 = 11 кН.
Проверка: ΣMA= 0:
ΣMA= q×8 × 4 + P×8 – YВ×16 = 0,5×8×4 + 20×8 – 11× 16 = 176 – 176 = 0.
Опорные реакции получились положительными. Это означает, что выбранные направления совпадают с их действительными направлениями.

Рис. 6
Построим эпюру моментов от амплитудного значения динамической нагрузки (рис. 7).
Уравнение моментов на ригеле DF (начало координат в точке D):
Мz(x) = 13x – 0,50,5x2 = 13x – 0,25x2.
при x = 0 Mz = 0;
при x = 8,0 м Mz = 138 – 0,25 82 = 104 – 16 = 88 кНм.
Так как в дальнейшем будем применять правило Верещагина, то эпюру на левой стойке рассматриваем как разность двух эпюр: от сосредоточенной нагрузки 13 кН – треугольник с катетом 104 кНм и от распределенной нагрузки парабола с максимальным значением 16 кНм.
Уравнение моментов на ригеле BG (начало координат в точке B):
Мz(x) = 11x.
при x = 0 Mz = 0;
при x = 8,0 м Mz = 118 = 88 кНм.
Уравнение моментов на участке GF стойки (начало координат в точке G):
Mz = 88 кНм;

Рис. 7
Далее определяем грузовые коэффициенты.
Перемножаем эпюру М1 (рис. 4) на грузовую эпюру:
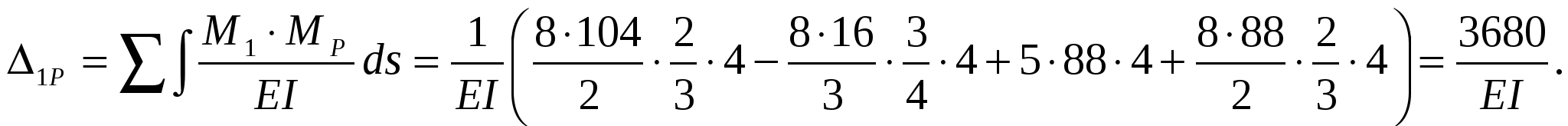
Перемножаем эпюру М2 (рис. 5) на грузовую эпюру:
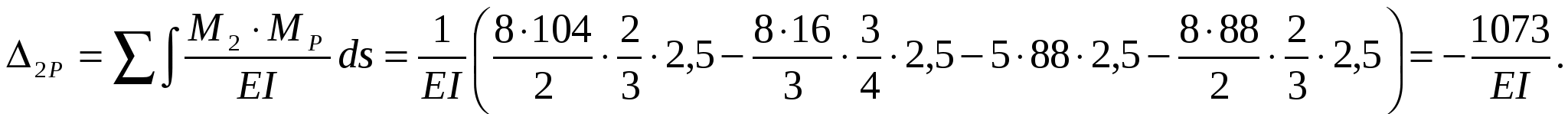
Подставляем найденные коэффициенты в канонические уравнение метода сил:
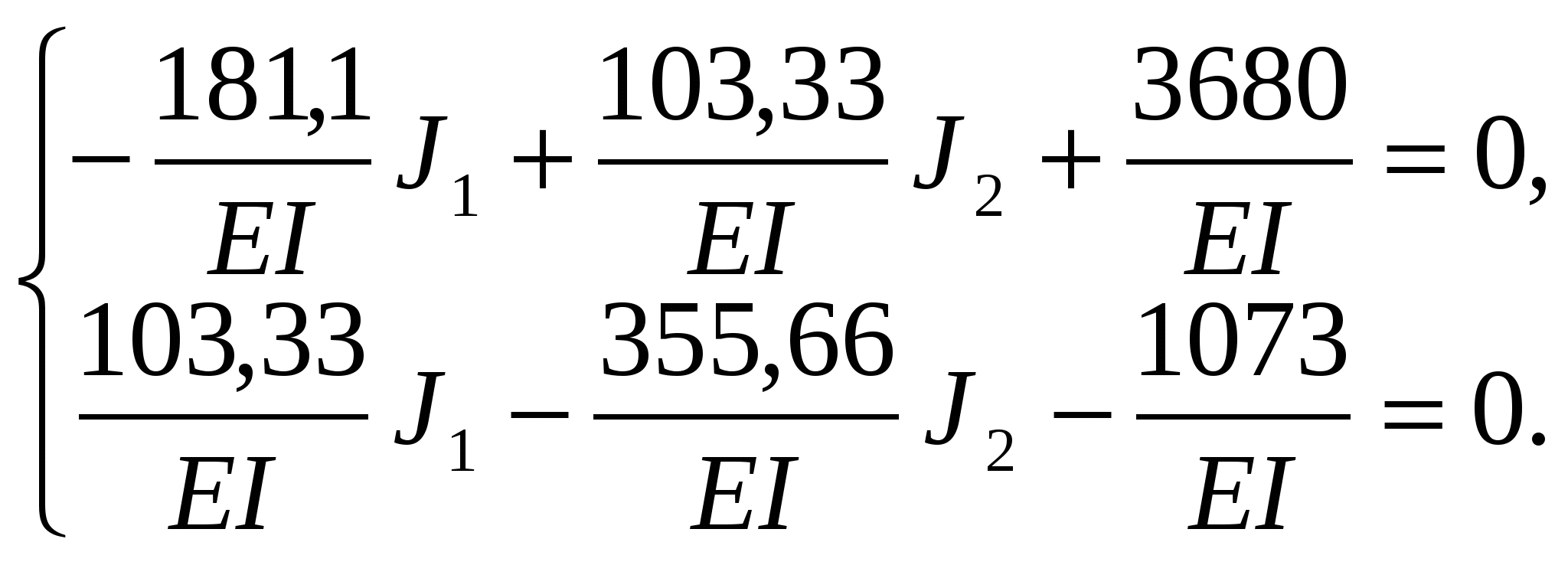
Решаем данную систему методом Крамера.
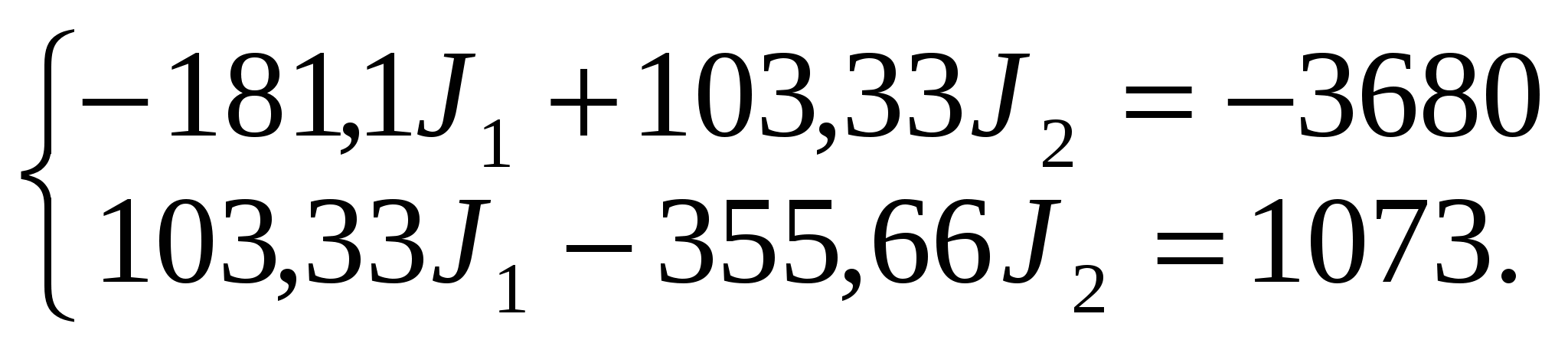
= 181,1 355,66 – 103,332 = 53733.
1 = 3680 355,66 – 1073103,33 = 1197922.
2 = -181,1 1073 + 103,333680 = 185874.
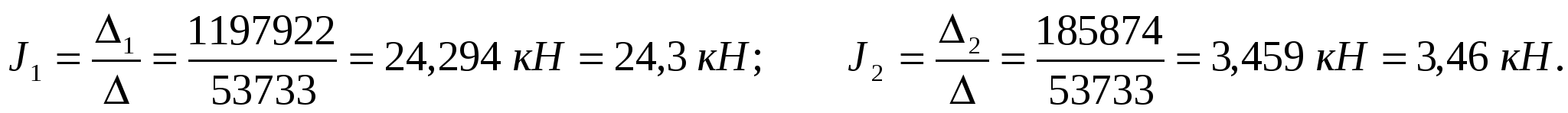
Вычислим опорные реакции при действии динамической нагрузки и сил инерции (рис 8,а).
Из уравнения ΣX= 0: J2 - XC = 0; XC = J2 = 3,46 кН.
ΣMС= YА16 – q8(4+8) – (P + J1)8 + J25 = 0.
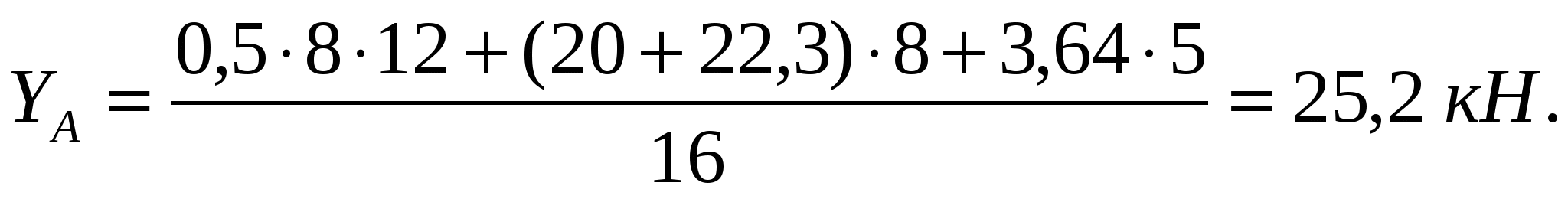
ΣY = YB +YA – q8 – P – J1 = 0.
YB = q8 + P + J1 – YA = 0,58 + 20 + 22,3 – 25,2 = 21,1 кН.
Проверка: ΣMA= 0:
ΣMA= q×8 × 4 + (P+ J1)×8 – YВ×16 + J25 – XC10 = 0,5×8×4 + (20 + 22,3) ×8 – 21,1× 16 +
+ 3,645 – 3,6410 = 372,6 – 372,6 = 0.
Опорные реакции получились положительными. Это означает, что выбранные направления совпадают с их действительными направлениями.
Построим динамическую эпюру моментов (рис. 8, б).
Уравнение моментов на ригеле DF (начало координат в точке D):
Мz(x) = 25,2x – 0,50,5x2 = 25,2x – 0,25x2.
при x = 0 Mz = 0;
при x = 8,0 м Mz = 25,28 – 0,25 82 = 201,8 – 16 = 185,8 кНм.
Так как в дальнейшем будем применять правило Верещагина, то эпюру на левой стойке рассматриваем как разность двух эпюр: от сосредоточенной нагрузки 25,2 кН – треугольник с катетом 201,8 кНм и от распределенной нагрузки парабола с максимальным значением 16 кНм.
Уравнение моментов на ригеле BG (начало координат в точке B):
Мz(x) = 21,1x.
при x = 0 Mz = 0;
при x = 8,0 м Mz = 21,18 = 168,5 кНм.
Уравнение моментов на участке GF стойки (начало координат в точке G):
Mz = 168,5 кНм;
Уравнение моментов на участке EF стойки (начало координат в точке E):
Mz = 3,64y.
при y = 0 Mz = 0; при y = 5,0 м Mz = 18,2 кНм.

Рис. 8
Уравнение поперечной силы на ригеле DF (рис. 8, в):
Q(x) = 25,2 – 0,5x.
при x = 0 Q = +25,2 кН; при x = 8,0 м Q = +21,2 кН.
На ригеле BG Q = -21,1 кН.
На стойке EF Q = -3,64 кН. На участке GF стойки Q = -21,1 кН.
Продольная сила на ригеле CE N = -3,64 кН. На стойке AD продольная сила N = –25,2 кН, на участке GF стойки продольная сила N = -21,1 кН.
Продольную силу на стойке EF вычислим исходя из того, что инерционная сила J1 приложена к двум массам m и 3m (рис. 1, 2), поэтому N = -P – 1J1/(1+3) = = -20 – 22,3/4 = -25,6 кН, или N = -YA + q8 – YB + 3J1/(1+3) = -25,2 + 0,58 – 21,1 + 322,3/4 = -25,6 кН.
Определяем динамические перемещения масс, перемножая эпюру М1 (рис. 4) на эпюру динамических моментов Mq1:
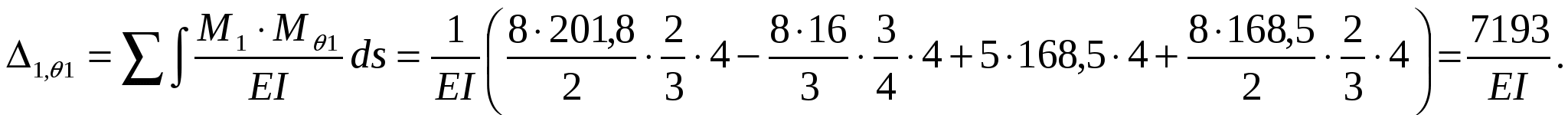
Перемножаем эпюру М2 (рис. 5) на эпюру динамических моментов Mq1:
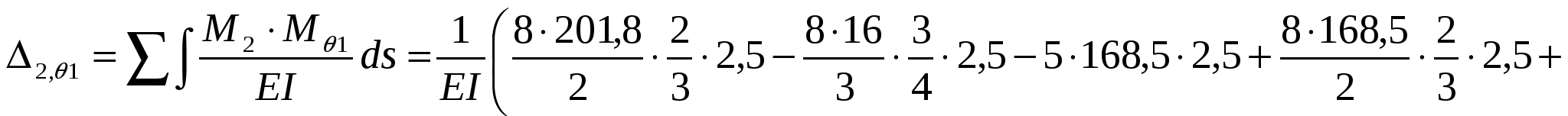 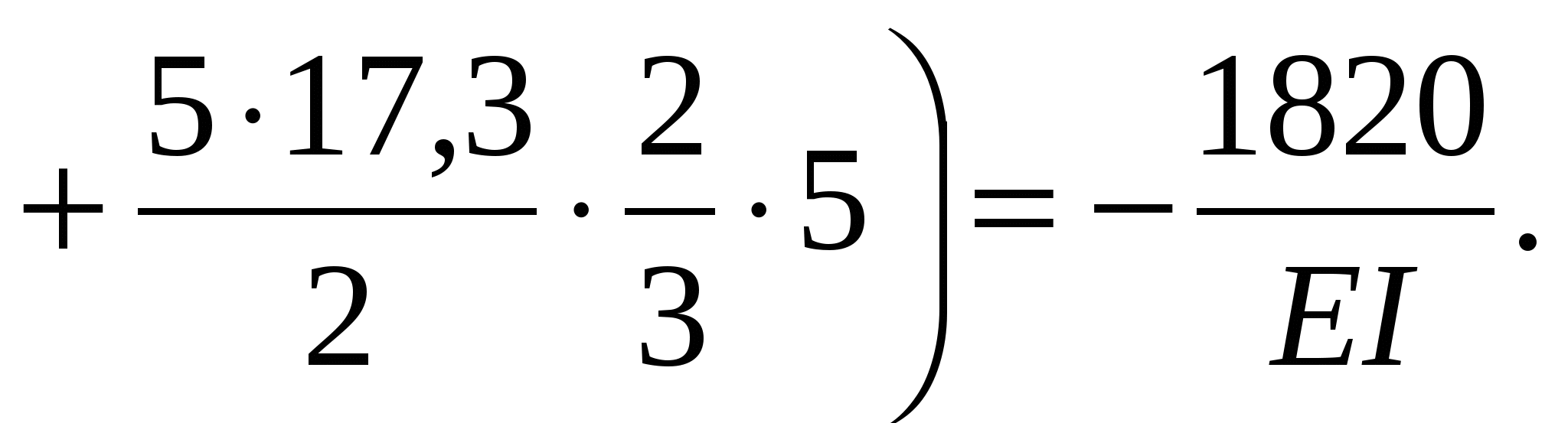
Для построения графика амплитудных значений сил инерции в зависимости от частоты вынужденных колебаний необходимо решить канонические уравнения при различных значениях частот нагрузки .
От частоты вынужденной нагрузки зависят только коэффициенты *ii. Найдем их значения при частоте

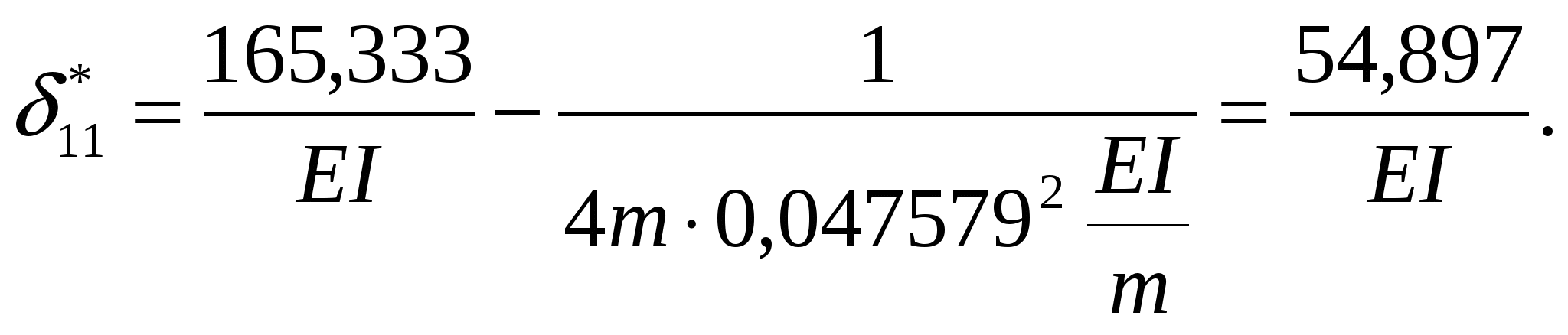
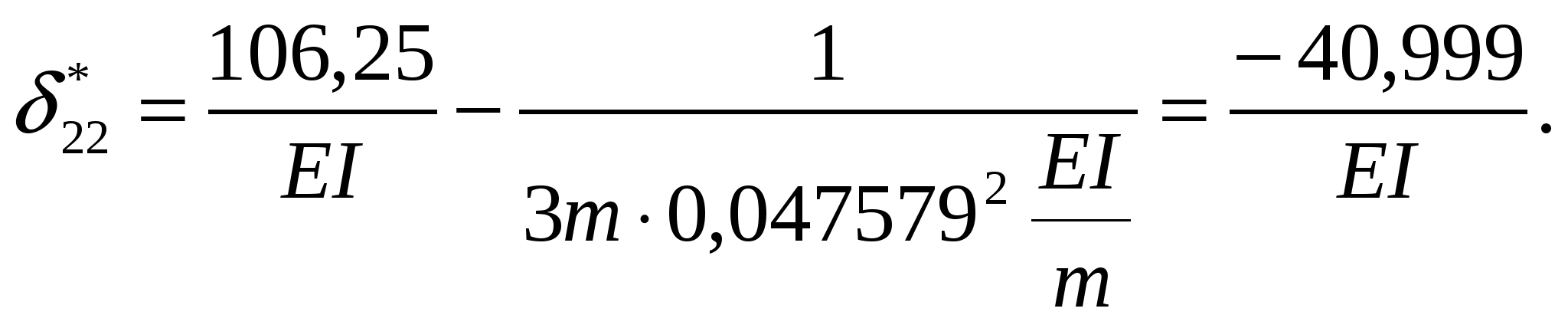
Подставляем найденные коэффициенты в канонические уравнение метода сил:
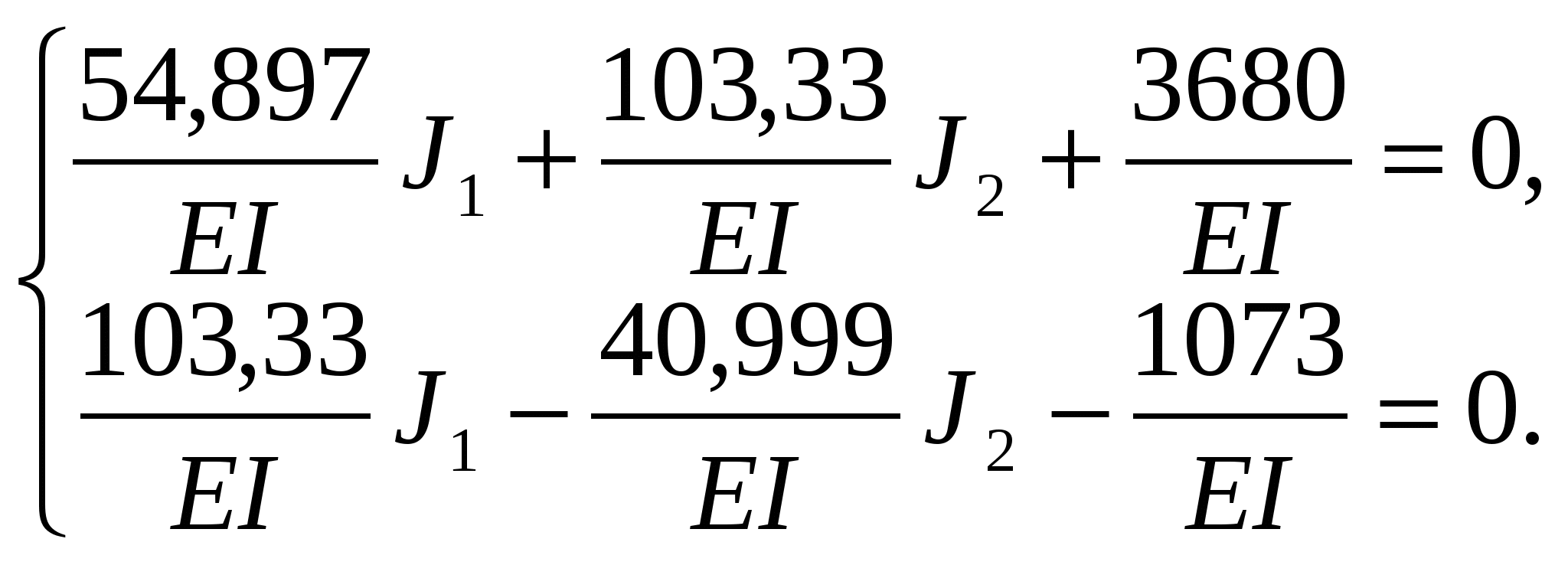
Решаем данную систему методом Крамера.
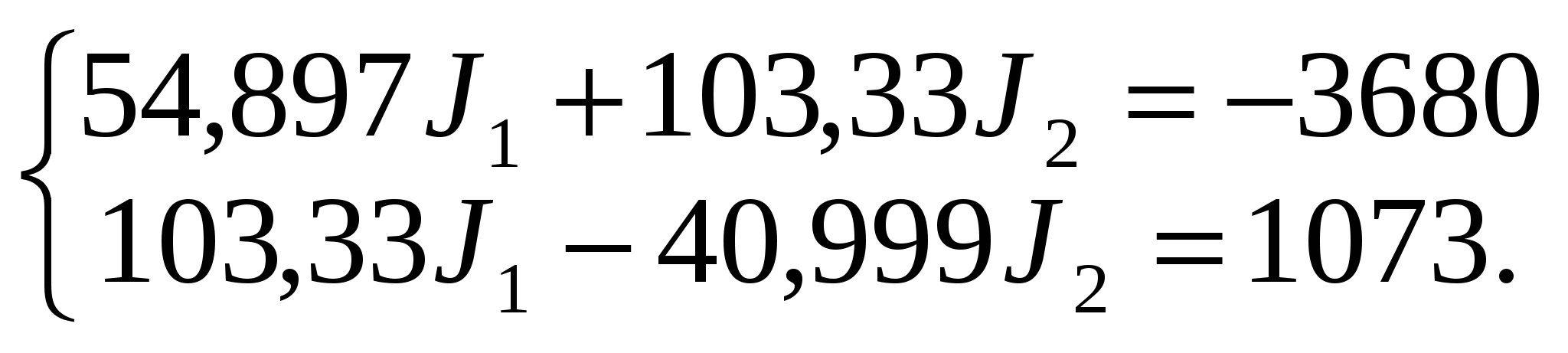
= -54,897 40,999 – 103,332 = -12928.
1 = 3680 40,99 – 1073103,33 = 39964.
2 = 54,897 1073 + 103,333680 = 439190.

Вычислим опорные реакции при действии динамической нагрузки и сил инерции (рис 9,а).
Из уравнения ΣX= 0: J2 - XC = 0; XC = J2 = 34,0 кН.
ΣMС= YА16 – q8(4+8) – (P – J1)8 – J25 = 0.
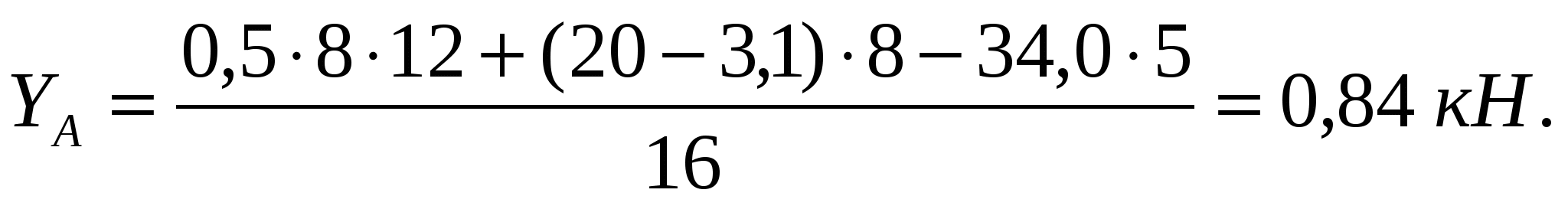
ΣY = YB +YA – q8 – P + J1 = 0.
YB = q8 + P – J1 – YA = 0,58 + 20 – 3,1 – 0,84 = 20,1 кН.
Проверка: ΣMA= 0:
ΣMA= q×8 × 4 + (P– J1)×8 – YВ×16 + XC 10– J25 = 0,5×8×4 + (20 – 3,1) ×8 – 20,1× 16 +
+ 34,010 – 34,05 = 491 – 491 = 0.
Опорные реакции получились положительными. Это означает, что выбранные направления совпадают с их действительными направлениями.
Построим динамическую эпюру моментов (рис. 9, б).
Уравнение моментов на ригеле DF (начало координат в точке D):
Мz(x) = 0,84x – 0,50,5x2 = 0,84x – 0,25x2.
при x = 0 Mz = 0; при x = 3,355 м Mz = 0;
при x = 8,0 м Mz = 0,848 – 0,25 82 = 6,7 – 16 = -9,3 кНм.
Так как в дальнейшем будем применять правило Верещагина, то эпюру на левой стойке рассматриваем как разность двух эпюр: от сосредоточенной нагрузки 0,84 кН – треугольник с катетом 6,7 кНм и от распределенной нагрузки парабола с максимальным значением 16 кНм.
Уравнение моментов на ригеле BG (начало координат в точке B):
Мz(x) = 20,1x.
при x = 0 Mz = 0; при x = 8,0 м Mz = 20,18 = 160,6 кНм.
Уравнение моментов на участке GF стойки (начало координат в точке G):
Mz = 160,6 кНм;
Уравнение моментов на участке EF стойки (начало координат в точке E):
Mz = 34,0y.
при y = 0 Mz = 0; при y = 5,0 м Mz = 169,9 кНм.
Уравнение поперечной силы на ригеле DF (рис. 9, в):
Q(x) = 0,84 – 0,5x.
при x = 0 Q = +0,84 кН; при x = 8,0 м Q = -3,16 кН;
при x = 1,677 м Q = 0; M = +0,703 кНм.
На ригеле BG Q = -20,1 кН. На стойке EF Q = +34,0 кН.
На участке GF стойки Q = -21,1 кН.
Продольная сила на ригеле CE N = +34,0 кН. На стойке AD продольная сила N = –0,84 кН, на участке GF стойки продольная сила N = -20,1 кН.
Продольную силу на стойке EF вычислим исходя из того, что инерционная сила J1 приложена к двум массам m и 3m (рис. 1, 2), поэтому N = -P + 1J1/(1+3) = -20 + 3,1/4 = -19,2 кН, или N = -YA + q8 - YB - 3J1/(1+3) = -0,84 + 0,58 - 20,1 - 33,1/4 = -19,2 кН.
Определяем динамические перемещения масс, перемножая эпюру М1 (рис. 4) на эпюру динамических моментов Mq2:
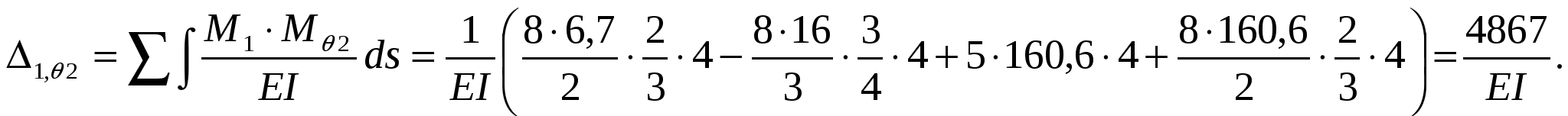
Перемножаем эпюру М2 (рис. 5) на эпюру динамических моментов Mq2:
 

Рис. 9 |
 Скачать 1.36 Mb.
Скачать 1.36 Mb.