ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ИСПОЛЬЗОВАНИЕМ БИПРИЗМЫ. ЛР№2. Определение длины световой волны с использованием бипризмы
 Скачать 269.12 Kb. Скачать 269.12 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра физики отчет по лабораторной работе №2 по дисциплине «Физика» Тема: Определение длины световой волны с использованием бипризмы
Санкт-Петербург 2020 Цель работы: Определение длины световой волны интерференционным методом. Общие сведения. Один из способов наблюдения интерференции световых волн основан на использовании бипризмы Френеля. Бипризма Френеля представляет собой две призмы с очень малым преломляющим углом , сложенные основаниями. 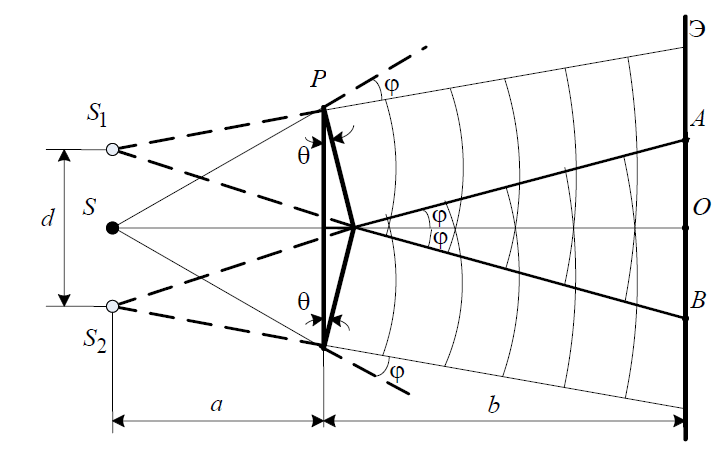 Схема наблюдения интерференционной картины с помощью бипризмы показана на рис. 2.1. Схема наблюдения интерференционной картины с помощью бипризмы показана на рис. 2.1.Рис. 2.1. Получение интерференционной картины с использованием бипризмы Френеля От источника света (щели) лучи падают на обе половины бипризмы Р, преломляются в ней и за призмой распространяются так, как если бы исходили из двух мнимых источников S1 и S2. Действительно, если смотреть через верхнюю половину бипризмы, то светящаяся щель S будет казаться расположенной в точке S1, а если смотреть через нижнюю половину бипризмы, то расположенной в точке S2. За призмой имеется область пространства, в которой световые волны, преломленные верхней и нижней половинами бипризмы, перекрываются (на рисунке 2.1 эта область заштрихована). В этой области пространства сводятся воедино две части каждого цуга волн от источника  , прошедшие разные оптические пути, способные при выполнении условия , прошедшие разные оптические пути, способные при выполнении условия  интерферировать, где интерферировать, где 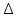 – разность хода лучей. Длина когерентности – разность хода лучей. Длина когерентности 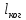 определяется как расстояние, которое проходит световая волна за время, при котором случайное изменение фазы волны не превышает определяется как расстояние, которое проходит световая волна за время, при котором случайное изменение фазы волны не превышает  . При превышении разностью хода длины когерентности волны в точку наблюдения приходят со случайной разностью фаз и интерференционная картина перестает быть видимой. . При превышении разностью хода длины когерентности волны в точку наблюдения приходят со случайной разностью фаз и интерференционная картина перестает быть видимой.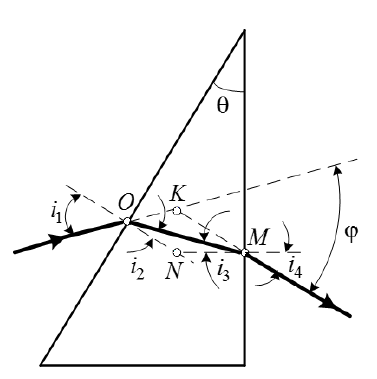 Интерференционная картина, получающаяся от бипризмы, соответствует интерференции волн, исходящих из двух когерентных источников, расположенных в точках S1 и S2. На экране Э, пересекающем заштрихованную область, тогда наблюдается ряд светлых и темных полос, параллельных ребру бипризмы. Светлые полосы лежат в тех местах экрана, куда приходят волны от источников S1 и S2 с разностью хода, равной целому числу длин волн, темные – в тех местах, куда приходят волны с разностью хода, равной нечетному числу полуволн. Расстояние Интерференционная картина, получающаяся от бипризмы, соответствует интерференции волн, исходящих из двух когерентных источников, расположенных в точках S1 и S2. На экране Э, пересекающем заштрихованную область, тогда наблюдается ряд светлых и темных полос, параллельных ребру бипризмы. Светлые полосы лежат в тех местах экрана, куда приходят волны от источников S1 и S2 с разностью хода, равной целому числу длин волн, темные – в тех местах, куда приходят волны с разностью хода, равной нечетному числу полуволн. Расстояние 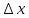 между светлыми (или темными) полосами интерференционной картины составляет между светлыми (или темными) полосами интерференционной картины составляет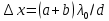 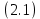 где a и b – соответственно расстояния от щели до бипризмы и от бипризмы до экрана; d – расстояние между мнимыми источниками (см. рис. 2.1).  Рис. 2.2. Ход луча через половину бипризмы ренеля Для определения расстояния d между мнимыми источниками рассмотрим ход луча через одну из половин бипризмы (рис. 2.2). Для точки О в соответствии с законом преломления 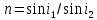 где где 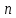 – показатель преломления материала призмы (стекла); – показатель преломления материала призмы (стекла); 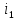 и и 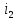 – углы падения и преломления. Вследствие малости углов справедливо – углы падения и преломления. Вследствие малости углов справедливо 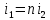 . Аналогично для точки . Аналогично для точки 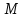 имеем имеем 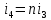 . Рассматривая треугольники . Рассматривая треугольники 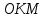 и и 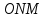 , можно показать, что справедливы соотношения , можно показать, что справедливы соотношения 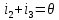 и и 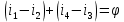 . Из этих соотношений для угла . Из этих соотношений для угла 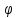 отклонения луча половиной бипризмы несложно получить отклонения луча половиной бипризмы несложно получить 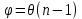 . . Таким образом, в рамках использованных допущений все лучи отклоняются каждой из половин бипризмы на одинаковый угол. Расстояние d, как видно из рис. 2.1, равно 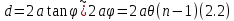 C учетом этого соотношения вместо выражения (1) имеем 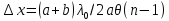 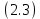 или 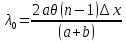 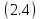 Выражения (2.3) или (2.4) устанавливают связь между длиной световой волны и геометрическими размерами системы (т.е. источник света – бипризма Френеля – экран), в которой реализуется явление интерференции. Видимость интерференционной картины зависит от размеров источника света, в чем нетрудно убедиться, изменяя ширину щели.  Рис. 2.3. Определение апертуры и угла схождения лучей в опыте с бипризмой Френеля Для интерференционного эффекта существенны, однако, не сами по себе размеры щели, а угол 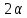 (рис. 2.3) между соответствующими лучами, идущими от S через каждую из двух ветвей интерферометра к точке О. Этот угол, который представляет собой угол раскрытия лучей, называется апертурой интерференции. Ему соответствует в поле интерференции угол схождения лучей (рис. 2.3) между соответствующими лучами, идущими от S через каждую из двух ветвей интерферометра к точке О. Этот угол, который представляет собой угол раскрытия лучей, называется апертурой интерференции. Ему соответствует в поле интерференции угол схождения лучей 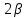 , величина которого связана с углом , величина которого связана с углом 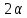 правилами построения изо- бражений. При неизменном расстоянии до экрана правилами построения изо- бражений. При неизменном расстоянии до экрана 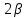 тем больше, чем больше тем больше, чем больше 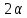 . .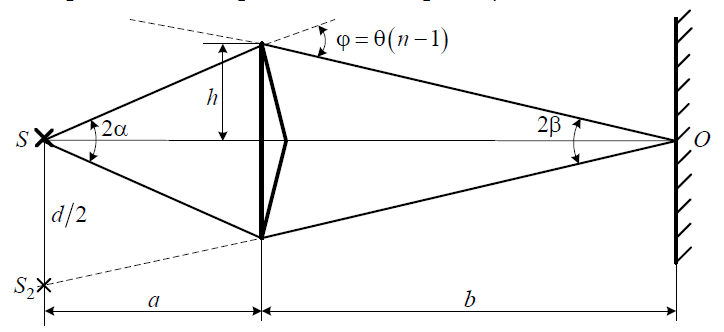 Из рис. 2.3 видно, что 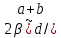 ) ) 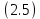 Подставляя выражение (2.5) в (2.1), получаем для расстояния между интерференционными полосами 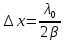 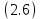 Из рис. 2.3 видно также, что 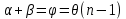 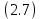 и, кроме того 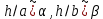 . Исключая из двух последних выражений величину h, получаем . Исключая из двух последних выражений величину h, получаем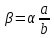 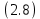 Из совместного рассмотрения выражений (2.7) и (2.8) находим 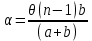 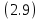 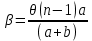 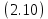 Эти соотношения будут использоваться далее для расчетов. Величина апертуры интерференции 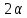 тесно связана с допустимыми размерами источника. Теория и опыт показывают, что с увеличением апертуры интерференции уменьшаются допустимые размеры ширины источника, при которых еще имеет место отчетливая интерференционная картина. Условие хорошего наблюдения интерференции от протяженного источника ширины тесно связана с допустимыми размерами источника. Теория и опыт показывают, что с увеличением апертуры интерференции уменьшаются допустимые размеры ширины источника, при которых еще имеет место отчетливая интерференционная картина. Условие хорошего наблюдения интерференции от протяженного источника ширины 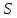 можно записать в виде: можно записать в виде: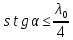 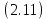 Это условие, несмотря на его приближенный характер, можно положить в основу расчетов допустимых размеров источника. В данной работе монохроматизация света осуществляется с помощью светофильтра. Нетрудно найти связь между порядком интерференции m и шириной спектрального интервала 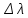 , пропускаемого светофильтром. Действительно, интерференция не будет наблюдаться, если максимум m-го порядка для , пропускаемого светофильтром. Действительно, интерференция не будет наблюдаться, если максимум m-го порядка для 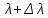 совпадет с максимумом совпадет с максимумом 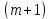 -го порядка для -го порядка для 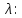 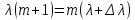 , т.е. , т.е.  .Для того чтобы интерференционная картина при данных значениях .Для того чтобы интерференционная картина при данных значениях 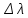 и и 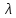 обладала высокой видимостью, приходится ограничиваться наблюдением интерференционных полос, порядок которых много меньше предельного обладала высокой видимостью, приходится ограничиваться наблюдением интерференционных полос, порядок которых много меньше предельного 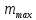 , определяемого условием , определяемого условием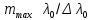 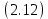 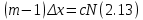 Экспериментальная установка состоит из оптической скамьи с мерной линейкой; бипризмы Френеля, закрепленной в держателе; источника света со светофильтром; раздвижной щели; окуляра со шкалой. Взаимное расположение элементов установки соответствует схеме, приведенной на рис. 2.1. Источником света служит лампа накаливания. Светофильтр, расположенный перед лампой, пропускает определенную часть спектра излучения лампы, которую и надлежит изучить. На оптической скамье, снабженной линейкой с миллиметровой шкалой, помещены укрепленные на держателях вертикальная щель S, бипризма Р и окуляр О. Ширину щели можно изменять с помощью винта, находящегося в верхней части его оправы. Щель и бипризма могут быть повернуты вокруг горизонтальной оси, а бипризма также и вокруг вертикальной оси. Для получения отчетливых интерференционных полос необходимо, чтобы плоскости щели и основания бипризмы были параллельны. Это достигается соответствующим поворотом бипризмы и/или щели. Окуляр О служит для наблюдения интерференционной картины. Для измерения расстояния между полосами он снабжен шкалой, цена малого деления которой составляет 0.1 мм. Протокол измерений.
𝛳=0.0061 рад n = 1.52 c = 0.1 мм/дел Контрольные вопросы. Какие волновые источники называются когерентными? Когерентные источники – источники волн, имеющие одинаковую частоту и постоянную разность фаз колебаний. Что называется оптической разностью хода волн? Если две интерферирующие волны испускаются одним источником света, то разность хода - это геометрическая разность длин путей, по которым два интерферирующих луча от одной точки источника достигли одной точки экрана. Обработка результатов. По формуле (2.13) рассчитаем величину x (c = 0,1 мм/дел): 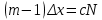 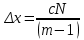 1) ∆x1 = 0,1*8/5 = 0,16 (мм) 2) ∆x2 = 0,1*8/5 = 0,16 (мм) 3) ∆x3 = 0,1*10/5 = 0,2 (мм) 4) ∆x4 = 0,1*5/4 = 0,13 (мм) 5) ∆x5 = 0,1*12/5 = 0,24 (мм) По формуле (2.4) для каждого опыта вычислим длину волны λ (𝛳=0.0061 рад, n = 1.52): 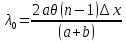 1) λ1 = 2*300*0.0061*0,52*0,16/550 = 0,00055 = 5,5*10-4 (мм) 2)λ2 = 2*310*0.0061*0,52*0,16/550 = 0,00057 = 5,7*10-4 (мм) 3)λ3 = 2*250*0.0061*0,52*0,2/550 = 0,00058 = 5,8*10-4 (мм) 4)λ4 = 2*370*0.0061*0,52*0,13/550 = 0,00055 = 5,5*10-4 (мм) 5) λ5 = 2*190*0.0061*0,52*0,24/550 = 0,00053 = 5,3*10-4(мм) Рассчитаем среднее значение длины волны фильтрованного света и доверительную погрешность : λ = {5,3*10-4; 5,5*10-4;5,5*10-4; 5,7*10-4; 5,8*10-4} (мм) N = 5, P = 95%; Up,n = 0,64 R = 5,8*10-4 - 5,3*10-4 = 0,5*10-4 (мм) U1= | λ1- λ2|/R = |5,3*10-4-5,5*10-4|/0,5*10-4 = 0,4 < 0,64 U2 = |5,5*10-4-5,5*10-4|/0,5*10-4 = 0 < 0,64 U3= |5,5*10-4-5,7*10-4|/0,5*10-4 = 0,4 < 0,64 U4= |5,7*10-4-5,8*10-4|/0,5*10-4 = 0,2 < 0,64 Промахов нет. λ̄ = (5,3*10-4+5,5*10-4+5,5*10-4+5,7*10-4+5,8*10-4)/5 = 5,56*10-4 (мм) = =556 (нм) Sλ̄ = 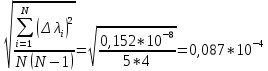 (мм) (мм) = 8,7 (нм) = 8,7 (нм)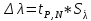 = 2,8 * = 2,8 *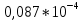 = 0,24*10-4 (мм) = 24 (нм) = 0,24*10-4 (мм) = 24 (нм)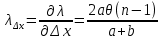 λ∆x1 = 34 (нм) λ∆x4 = 42 (нм) λ∆x2 = 35 (нм) λ∆x5 = 21 (нм) λ∆x3 =28 (нм) λ̄∆x= 160/5 = 32 (нм)=0,000032 (мм), Θ∆x= 0,005 (мм) = 500 (нм) 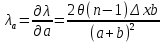 λa1 = 0,8 (нм) λa4 =0,5 (нм) λa2 = 0,8 (нм) λa5 =1,8 (нм) λa3 = 1,2 (нм) λ̄a = 5,1/5 = 1,02 (нм) = 1,02*10-6 (мм), Θa = 5 (мм) = 5*106 (нм) 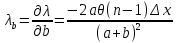 λb1 = -1,01 (нм) λb4 = -1,01 (нм) λb2 = -1,04 (нм) λb5 = -0,96 (нм) λb3 = -1,05 (нм) λ̄b = -5,07/5 = -1,01 (нм)= -1,01*10-6 (мм) Θb = 5 (мм) = 5*106 (нм) 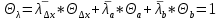 (нм) (нм)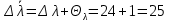 (нм) (нм)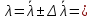 556 556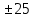 (нм) (нм) Вычислим по формулам (2.9) и (2.10) для первого опыта апертуру интерференции и угол схождения лучей : 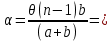 1,4*10-3 (рад) 1,4*10-3 (рад)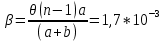 (рад) (рад)Оценим допустимые размеры источника (ширину щели s) для данной апертуры . 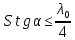 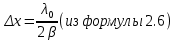 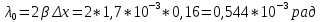 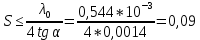 (мм) (мм)П 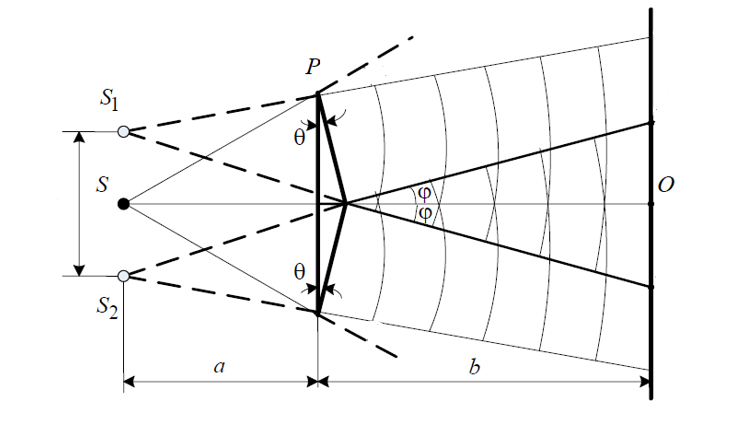 о формуле (2.12) оценить полосу пропускания светофильтра: о формуле (2.12) оценить полосу пропускания светофильтра: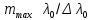 , , 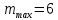 , , 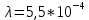 (из 1 опыта) (из 1 опыта)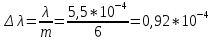 (мм) (мм)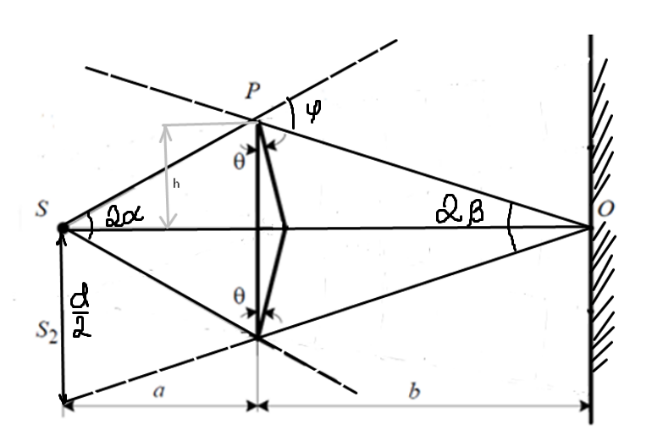 Вывод: я определила длину световой волны интерференционным методом, и получила результаты 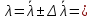 556 556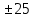 (нм), рассчитала величину x для каждого из опытов, вычислила апертуру интерференции =1,4*10-3 (рад) и угол схождения лучей = (нм), рассчитала величину x для каждого из опытов, вычислила апертуру интерференции =1,4*10-3 (рад) и угол схождения лучей =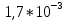 (рад), оценила допустимые размеры источника (S≤0,09 мм) и полосу пропускания светофильтра (=0,92*10-4 мм), а также сделала чертеж хода лучей. (рад), оценила допустимые размеры источника (S≤0,09 мм) и полосу пропускания светофильтра (=0,92*10-4 мм), а также сделала чертеж хода лучей. |
