Определение длины волны света с помощью дифракционной решетки
 Скачать 197 Kb.
|
|
Государственное образовательное учреждение высшего профессионального образования "ВОРОНЕЖСКАЯ ГОСУДАРСТВЕННАЯ МЕДИЦИНСКАЯ АКАДЕМИЯ им. Н.Н. БУРДЕНКО"
КАФЕДРА МЕДИЦИНСКОЙ ФИЗИКИ Методические указания студентам по теме лабораторного занятия ОПРЕДЕЛЕНИЕ ДЛИНЫ ВОЛНЫ СВЕТА С ПОМОЩЬЮ ДИФРАКЦИОННОЙ РЕШЕТКИ Воронеж 2009 РАЗДЕЛ: ОПТИКА ТЕМА: Определение длины волны света с помощью дифракционной решетки. ЦЕЛЬ: Знать и понимать сложную природу света. Изучить волновые и квантовые аспекты теории света. Рассмотреть теоретические вопросы интерференции и дифракции. ПРАКТИЧЕСКИЕ НАВЫКИ: Научиться использовать полученные знания для оценки технических возможностей спектральных приборов, в частности, дифракционной решетки. Уметь определить длину волны света по спектру от дифракционной решетки, оценить точность полученного результата. МОТИВАЦИЯ ТЕМЫ: Понимание сложной природы света необходимо для успешного изучения физиологии зрения и глазных болезней. Подтверждением двойственной природы света является в частности тот факт, что глаз проявляет различную спектральную чувствительность к световой волне и в то же время чувствительность зрительного рецептора позволяет реагировать на отдельный фотон света. Полученные в данной работе практические навыки помогут в дальнейшем освоить методику работы с оптическими приборами. Например, с интерферометрами, позволяющими с большой точностью определять показатели преломления, исследовать качество поверхностей, измерять толщину слоя вещества. Явление интерференции в тонких пленках используется для просветления оптики, в интерференционных светофильтрах и т. д. I. САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ ВО ВНЕУРОЧНОЕ ВРЕМЯ. Задание 0. Повторить теоретический материал школьного курса физики, раздел " Электромагнитные волны" по следующей схеме: 1. Понятие электромагнитной волны. 2. Основные параметры, используемые для характеристики волн, связь скорости волны с ее длиной. 3. Энергетические характеристики электромагнитной волны. 4. Плотность потока излучения. Зависимость плотности потока энергии электромагнитной волны от расстояния до источника. Зависимость плотности потока излучения от частоты. Задание 1. Изучить теоретический материал занятия, используя рекомендованную литературу и настоящую методическую разработку, по следующей логической структуре учебного материала: 1. Понятие интерференции света, когерентных волн, сложение волн, формула амплитуды результирующей волны. 2. Понятие разности фаз и оптической разности хода слагаемых волн. 3. Связь между разностью фаз и оптической разностью хода интерферирующих волн, условия максимума и минимума интенсивности света при интерференции по разности фаз и по разности хода волн. 4. Просветление оптики, формула для расчета толщины просветляющей пленки. 5. Интерферометры и их применение. 6. Принцип Гюйгенса-Френеля, понятие дифракции, зоны Френеля. 7. Дифракция на щели в параллельных лучах. 8. Дифракционная решетка, период и вывод формулы дифракционной решетки, порядок главных максимумов. 9. Порядок спектра, угловая дисперсия, разрешающая способность дифракционной решетки. Средства для самоподготовки студентов во внеурочное время 1. Учебная и методическая литература а) основная – Ремизов А.Н. Медицинская и биологическая физика / А.Н. Ремизов, А.Г. Максина, А.Я. Потапенко. – М.: Дрофа, 2007. – С. 338-357. – Лекционный материал по разделу "Оптика". б) дополнительная – Федорова В.Н., Степанова Л.А. Краткий курс медицинской и биологической физики с элементами реабилитологии. Лекции и семинары. – М.:ФИЗМАТЛИТ, 2005. – С. 310-328. 2. Консультации преподавателей (еженедельно по индивидуальному графику). ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ ПО ТЕМЕ ЗАНЯТИЯ Современная теория света основывается на том, что природа света электромагнитная и в интервале от 760 нм (красный) до 400 нм (фиолетовый) свет обладает в равной степени и волновыми и корпускулярными свойствами. Подтверждением корпускулярных свойств является фотоэффект, люминисценция и другие явления. Интерференция и дифракция свойственны волновому процессу. Под явлением интерференции понимают такое сложение волн, в результате которого образуется устойчивая картина распределения в пространстве областей максимумов и минимумов. Необходимым условием интерференции является когерентность волн. Когерентными волнами являются волны с одинаковыми частотами и с постоянной по времени разностью фаз. Если две волны распространяются в пространстве и свойства среды, заполняющей пространство, при этом не меняются, то выполняется принцип суперпозиции, т.е. в некоторой точке результирующее колебание представляет собой геометрическую сумму слагаемых колебаний, соответствующих каждой из волн. Амплитуда результирующего колебания может быть вычислена по формуле:
где А1 – амплитуда первой волны, А2 – амплитуда второй волны, 1, 2 – фазы первой и второй волн в той точке, где определяем амплитуду Арезультирующего колебания. В точках, где разность фаз слагаемых волн равна четному числу π, получим из формулы (1) максимум амплитуды:
Тогдаусловие максимума интенсивности (max) света при интерференции по разности фаз:
т.е. в этих точках наблюдается наибольшее усиление волн. В точках, где разность фаз слагаемых волн равна нечетному числу π, получим из формулы (1) минимум амплитуды:
Тогдаусловие минимума интенсивности (min) света при интерференции по разности фаз:
т.е. в этих точках наблюдается ослабление волн и полное их гашение при А1 = А2. Произведение геометрического пути волны на показатель преломления среды, т.е. xn, называют оптической длиной пути, а разность этих путей – оптической разностью хода волн:
Связь между разностью фаз и оптической разностью хода интерферирующих волн:
Известно, что фазе, = π соответствует пройденный волной путь, равный  . Тогда условие максимумов можно сформулировать так: максимальное усиление результирующего колебания наступает, если оптическая разность хода слагаемых волн равна четному числу полуволн или целому числу длин волн, т. е.
Условие минимумов: ослабление результирующего колебания будет, если оптическая разность хода слагаемых волн равна нечетному числу полуволн, т. е.
где k = 0, 1, 2, … – порядок главных максимумов или минимумов. Совокупность максимумов (минимумов) представляет собой некоторые поверхности, вид которых зависит от свойств источников и их взаимного расположения. По изменению интерференционной картины можно на практике определить качество оптической поверхности. Интерференцию света используют для измерения показателя преломления веществ, длины волны света, малых расстояний, а также для просветления оптики. Просветление оптики – специальный прием, имеющий цель уменьшить потери на отражение. Сущность его заключается в том, что оптические поверхности покрываются тонкими пленками, создающими интерференционные явления. Наибольшее просветляющее действие получается при условии, что показатель преломления на границе среда – пленка равен показателю преломления на границе пленка – линза.
где nср. – показатель преломления среды; nпл. – показатель преломления пленки; nлин. – показатель преломления линзы. При выполнении условия (6) и условия минимумов при интерференции на пленке световой поток проходит сквозь оптическую поверхность без потерь на отражение. Наименьшая толщина пленки (d) при этом может быть определена по формуле:
где λ – длина волны света; nпл. – показатель преломления пленки. На практике часто применяют многослойные пленки для обеспечения просветляющего действия в некотором диапазоне длин волн и углов падения. Дифракцией называют явление отклонения волны от прямолинейного распространения в среде с резкими неоднородностями, т.е. явление, связанное с отклонением от законов геометрической оптики. Наглядно представить механизм возникновения дифракции позволяет принцип Гюйгенса-Френеля. Этот принцип состоит в том, что каждую точку среды, до которой дошла волна, можно рассматривать как источник элементарных вторичных волн. Огибающая этих элементарных волн будет поверхностью волны в другой, близкий момент времени. В боковых направлениях волны взаимно гасятся по закону интерференции. Дифракция наблюдается при распространении света вблизи резких краев непрозрачных тел, сквозь узкие отверстия и, вообще, в среде с резкими неоднородностями, особенно, если размеры неоднородностей порядка длины волны. Дифракция свойственна любым волнам и наблюдается одновременно с интерференцией. Если необходимо узнать результат дифракции в некоторой точке пространства, то необходимо сложить все волны, пришедшие в эту точку, т.е. посмотреть по законам интерференции, что получится в результате сложения. В случае волновой поверхности произвольной формы расчет окажется сложным. В случае плоской волны вычисления проще. При этом можно использовать метод зон Френеля. При этом волновую поверхность разбивают на отдельные участки (зоны Френеля). Рассмотрим дифракционный спектр от щели в параллельных лучах (рис. 1.)  Рис. 1. Распределение интенсивности света за щелью Если в ширине щели укладывается нечетное число зон Френеля, то в центре дифракционного спектра образуется максимум:
В случае четного числа зон Френеля от щели получится дифракционный спектр с центральным минимумом:
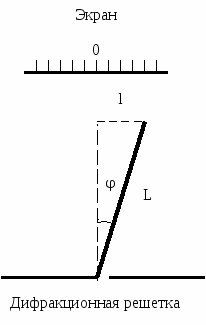
где a – ширина щели; – угол дифракции, отсчитываемый от нормали; – длина волны. Дифракционный спектр от системы щелей будет результатом наложения спектров от отдельных щелей. На рис. 2 представлен вид дифракционного спектра от одной, двух и четырех щелей. Число промежуточных минимумов равно (N-1), где N – число щелей. При числе щелей более 15 промежутки между главными максимумами будут практически выглядеть темными – сплошной минимум. Спектр дифракционной решетки будет представлен главными максимумами, разделенными темными промежутками. 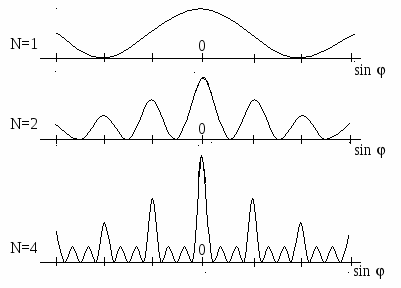 Рис. 2. Распределение интенсивности света после прохождения системы из N щелей Вывод формулы дифракционной решетки Дифракционная решетка – оптическое устройство, представляющее собой совокупность большого числа параллельных, обычно равностоящих друг от друга щелей. Дифракционную решетку можно получить нанесением непрозрачных царапин (штрихов) на стеклянную пластину. Непроцарапанные места – щели – будут пропускать свет, штрихи – рассеивать и не пропускать (рис. 3).  Рис. 3. Сечение дифракционной решетки (а) и ее графическое изображение (б) Для вывода формулы рассмотрим дифракционную решетку при условии перпендикулярного падения света (рис. 4). Выберем два параллельных луча, прошедших две щели и направленных под углом φ к нормали. С помощью собирающей линзы (глаза) эти два луча попадут в одну точку фокальной плоскости Р и результат их интерференции будет зависеть от разности фаз или от их разности хода. Если линза стоит перпендикулярно лучам, то разность хода будет определяться отрезком ВС, где АС – перпендикуляр к лучам А и В. В треугольнике АВС имеем: АВ = а + b = d – период решетки, ВАС = φ, как углы с взаимно перпендикулярными сторонами.
Лучи А и В дадут интерференционный максимум, если выполнится условие (4), т.е.
Из формул (8) и (9) получим формулу дифракционной решетки:
 Рис. 4. Дифракция света на дифракционной решетке Т.е. положение световой линии в дифракционном спектре не зависит от вещества решетки, а определяется периодом решетки, который равен сумме ширины щели и промежутка между щелями. Разрешающая способность дифракционной решетки. Если свет, падающий на дифракционную решетку полихроматический, т.е. состоит из нескольких длин волн, то в спектре максимумы отдельных будут под разными углами. Характеризовать разрешение можно угловой дисперсией:
где d – угловое расстояние между двумя линиями спектра, которые имеют разность длин волн равную d. При дифференцировании формулы дифракционной решетки получим, что дисперсия равна:
Следовательно, угловая дисперсия тем больше, чем больше порядок спектра k. II. РАБОТА СТУДЕНТОВ ВО ВРЕМЯ ПРАКТИЧЕСКОГО ЗАНЯТИЯ. Задание 1. Получить допуск к занятию. Для этого необходимо: – иметь конспект в рабочей тетради, содержащий название работы, основные теоретические понятия изучаемой темы, задачи эксперимента, таблицу по образцу для внесения экспериментальных результатов; – успешно пройти контроль по методике проведения эксперимента; – получить у преподавателя разрешение выполнять экспериментальную часть работы. Задание 2. Выполнение лабораторной работы, обсуждение полученных результатов, оформление конспекта. Приборы и принадлежности
1. Дифракционная решетка. 2. Источник света. 3. Экран. 4. Линейка. В данной лабораторной работе предлагается определить длины волн для красного и зеленого цветов, которые получаются при прохождении света через дифракционную решетку. При этом на экране наблюдается дифракционный спектр. Дифракционная решетка состоит из большого числа параллельных щелей, очень малых по сравнению с длиной волны. Щели позволяют проходить свету, в то время как пространство между щелями непрозрачно. Общее количествощелей – N, с расстоянием между их центрами – d. Формула дифракционной решетки:
где d – период решетки; sin φ – синус угла отклонения от прямолинейного распространения света; k – порядок максимума; λ – длина волны света. Экспериментальная установка состоит из дифракционной решетки, источника света и подвижного экрана с линейкой. На экране наблюдается дифракционный спектр (рис. 5). Расстояние от дифракционной решетки до экрана L может изменяться перемещением экрана. Расстояние от центрального луча света до отдельной линии спектра l. При малых углах φ:
Тогда из формулы дифракционной решетки получим:
Выполнение работы 1. Определить длину волны красного света по максимумам первого и второго порядка от дифракционной решетки, период которой d = 0,01 мм. 1.1. Включить установку. 1.2. Для расстояний L = 30 и 45 см определите расстояние l слева и справа от центрального луча на экране со шкалой для красного света, используя первый и второй порядки максимумов (k = 1, 2). 1.3. По формуле (13) рассчитать длину волны данной линии спектра и внести полученные результаты в таблицу 1. 1.4. Используя данные таблицы, рассчитать среднюю величину длины волны красного света по формуле:
Таблица 1.
1.5. Рассчитать абсолютную и относительную погрешности для всех четырех измерений λ, а затем найти средние значения погрешностей. 1.5.1. Относительная погрешность каждого опыта:
где k = 1, 2, 3, 4;  – абсолютная погрешность при измерении расстояний l; ∆L = 1 мм – абсолютная погрешность при измерении расстояния L (в данном случае берем инструментальную погрешность шкалы).1.5.2. Абсолютная погрешность:
1.6. Записать полученный результат определения длины волны красного света в виде:
2. Определить длину волны зеленого света по максимумам первого и второго порядка по алгоритму (пункты 1.2.–1.6.) и составить таблицу 2. 3. Определить на какую величину отличаются длины волн двух линий в спектре, расположенных на расстоянии равном пределу разрешения глаза (Z = 0,2 мм). 3.1. Вычислить разность длин волн красного и зеленого света для одного максимума ∆λ = λкр. – λзел. 3.2. Вычислить соответствующую разность расстояний ∆l = lкр. – lзел. 3.3. Оценить величину линейной дисперсии дифракционной решетки по формуле:  4. Найти зависимость линейной дисперсии дифракционной решетки от порядка максимума и в тетради записать результаты исследований. 5. Подготовить письменный отчет по работе, который должен содержать формулы и результаты измерений, занесенные в таблицы, с анализом исследуемых процессов. Задание 3. Контроль конечного уровня знаний: устно-речевой отчет по выполненной лабораторной работе. Задание 4. Задание на следующее занятие: раздел и тема занятия. |
или 
,
,
,
, следовательно 
