1 лаба по кэту. 1 кошачий. Определение эксплуатационных характеристик пассивных элементов электронной техники
 Скачать 45.63 Kb. Скачать 45.63 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра микро- и наноэлектроники отчет по лабораторной работе № 1 по дисциплине «Компоненты электронной техники» Тема: Определение эксплуатационных характеристик пассивных элементов электронной техники
Санкт-Петербург 2021 ЛАБОРАТОРНАЯ РАБОТА №1 ОПРЕДЕЛЕНИЕ ЭКСПЛУАТАЦИОННЫХ ХАРАКТЕРИСТИК ПАССИВНЫХ ЭЛЕМЕНТОВ ЭЛЕКТРОННОЙ ТЕХНИКИ ЦЕЛЬ: исследование пассивных элементов электронной техники ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ Пассивные элементы электронной техники – конденсаторы, резисторы и катушки индуктивности – служат для перераспределения и регулирования напряжений, токов и мощностей в отдельных участках электрических схем. К основным параметрам конденсатора относят номинальную емкость Сном, температурный коэффициент емкости ТКЕ, тангенс угла потерь tg δC. Номинальная (расчетная) емкость конденсатора зависит от его конструкции, геометрических размеров, а также от диэлектрической проницаемости используемого в нем диэлектрика. Точность, с которой обеспечивается получение номинальной емкости, характеризуется значением допуска в процентах относительно номинала. Температурный коэффициент емкости αC(или ТКЕ) отражает отклонение емкости, обусловленное изменением температуры, и, следовательно, характеризует температурную стабильность емкости конденсатора. Общее определение этого параметра соответствует выражению 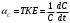 (1) (1)Нормировать (задать) αCконденсатора можно в том случае, если зависимость емкости конденсатора от температуры носит линейный характер, что имеет место для конденсаторов, в которых используются материалы с мгновенными видами поляризации (электронная и ионная). В зависимости от того, какой из этих видов поляризации преобладает, ТКЕ будет иметь положительный или отрицательный знак. Тогда, задав при комнатной температуре tкомн номинальную емкость Сном и αС, можно определить емкость при любой другой температуре t (с учетом знака αС): 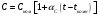 (2) (2)Применяя конденсаторы при высоких частотах, необходимо учитывать, что конденсатор имеет некоторое активное сопротивление r и некоторую собственную индуктивность LC. Для того, чтобы учесть наличие в конденсаторе r и LC, кроме его емкости С, вместо реактивного сопротивления xCнадо пользоваться полным сопротивлением конденсатора 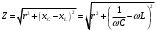 (3) (3)При увеличении частоты хСснижается, а хLрастет, поэтому зависимость полного сопротивления конденсатора от частоты должна иметь U-образный характер. При частоте выше резонансной конденсатор ведет себя уже не как емкость, а как индуктивность: 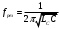 (4) (4)Практически о емкости конденсатора судят по величине переменного тока I, протекающего через конденсатор при подаче на него переменного напряжения U (очевидно, что I = U/Z). Частотные свойства конденсатора можно также охарактеризовать его эффективной емкостью Сэф, определяемой из соотношения Z = 1/(ωCэф). Если в конденсаторе ωL >> r, то 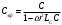 (5) (5)Если емкость с частотой уменьшается, то это может быть объяснено снижением ε диэлектрика с замедленными видами поляризации (полярные полимеры, сегнетокерамика) или влиянием активного последовательного сопротивления, что наблюдается в оксидных конденсаторах. Если r >> ωL, то 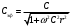 (6) (6)Собственная индуктивность конденсатора может быть определена по формуле 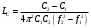 (7) (7)Частотная стабильность конденсаторов характеризуется величиной 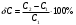 (8) (8)В конденсаторах с мгновенными видами поляризации потери в диэлектриках обусловлены сквозной электропроводностью, тогда тангенс угла потерь можно рассчитать из выражения: 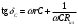 (9) (9)В сегнетокерамических конденсаторах наблюдается изменение емкости при изменении величины приложенного напряжения, которое можно оценить коэффициентом напряжения 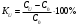 (10) (10)В свою очередь, резисторы не являются чисто активными сопротивлениями R = Rном – для них характерно наличие собственной индуктивности LR(включена последовательно с R) и собственной емкости СR(включена параллельно R). Обычно 1 / (ω CR) >> R и полное сопротивление резистора 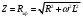 (11) (11)Величина LRзависит от конструкции и габаритов резисторов (максимальной LRобладают проволочные резисторы и пленочные резисторы со спиральной нарезкой). Частотная стабильность резисторов может быть охарактеризована величиной 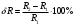 (12) (12)Для композиционных резисторов влияние на частотную стабильность может оказывать и собственная емкость резистивного элемента. Катушки индуктивности также имеют собственную параллельную емкость CLи последовательное активное сопротивление обмотки Rоб, которое зависит от частоты. Эффективная индуктивность катушки находиться из выражения 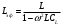 (13) (13)Потери в катушках индуктивности принято характеризовать добротностью Q 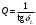 (14) (14)ОБРАБОТКА РЕЗУЛЬТАТОВ Из зависимостей, полученных в эксперименте 1.5.4 можно сделать вывод о том, что зелёный резистор с отверстием обладает большей частотной устойчивостью, чем конденсатор и катушка, но в эксперименте 1.5.3, проводимом на 2-х частотах (100 Гц и 1МГц) среди еще 2-х резисторов обладает самой малой частотной устойчивостью (по 2-м точкам). Так же по зависимостям, полученных в эксперименте 1.5.4 можно сделать вывод о том, что модуль иммитанса у конденсатора с ростом частоты падает, а у катушки волнообразная зависимость с значительным ростом в частотном диапазоне (5кГц – 200кГц). По данным эксперимента 1.5.3 можно сделать вывод, что прямоугольный конденсатор не пригоден для использования на высоких частотах т.к. на частоте 1 МГц проявляет индуктивные свойства и, что торообразная катушка не пригодна для использования на высоких частотах т.к. на частоте 1 МГц проявляет свойства конденсатора. Если опираться на данные обоих экспериментов, то можно сделать вывод, что устойчивее всего к высоким частом белый резистор т.к. во втором эксперименте резистивный элемент проявил высокую частотную устойчивость из конденсатора резистора и катушки. А в 1 эксперименте среди всех резисторов самый устойчивый белый. ВЫВОД: в ходе выполнения обработки результатов были построены частотные зависимости модуля иммитанса для исследуемых пассивных элементов электронной техники. По полученным зависимостям сделан вывод о целесообразности использования некоторых элементов на высоких частотах. |
