биби. Определение интегралов зависящих от параметра
 Скачать 206.9 Kb. Скачать 206.9 Kb.
|
|
Определение интегралов зависящих от параметра Пусть функция 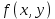 определена в прямоугольнике определена в прямоугольнике 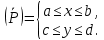 Пусть при каждом закрепленном Пусть при каждом закрепленном  из из  существует существует 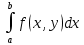 . Ясно, что каждому значению . Ясно, что каждому значению  из из  будет отвечать свое, вполне определенное значение этого интеграла. Следовательно будет отвечать свое, вполне определенное значение этого интеграла. Следовательно 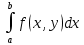 представляет собой функцию переменной (параметра) представляет собой функцию переменной (параметра)  , определенную в промежутке , определенную в промежутке  . .Введем обозначение 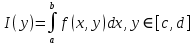 (1) (1)Наша задача будет состоять в том, чтобы, зная свойства функции 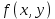 , получить информацию о свойствах функции , получить информацию о свойствах функции  . Эти свойства, как будет показано ниже, имеют многообразные применения в особенности при вычислении интегралов. . Эти свойства, как будет показано ниже, имеют многообразные применения в особенности при вычислении интегралов. Допустим еще, что при каждом закрепленном 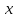 из из 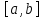 существует существует 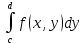 . Тогда этот интервал будет представлять собой функцию переменной (параметра) . Тогда этот интервал будет представлять собой функцию переменной (параметра) 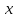 , определенную в промежутке , определенную в промежутке 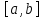 . Обозначим ее через . Обозначим ее через 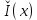 , так что , так что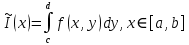 ( ( ) )О допустимости предельного перехода по параметру под знаком интеграла Теорема. Пусть функция 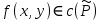 и пусть и пусть 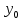 - любое из - любое из  . Тогда. . Тогда. 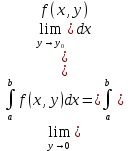 (1) (1)Отметим, что 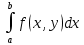 существует для каждого значения существует для каждого значения  из из  , так как , так как 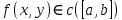 при любом закрепленном при любом закрепленном  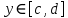 . В частности существует . В частности существует 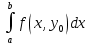 . .Возьмем 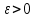 - любое. Выберем и закрепим любое - любое. Выберем и закрепим любое 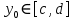 . .По условию 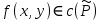 , поэтому , поэтому 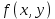 равномерно непрерывна в равномерно непрерывна в 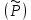 , и, следовательно, взятому , и, следовательно, взятому 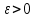 отвечает отвечает 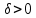 , зависящее только от , зависящее только от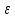 , такое, что для любых двух точек , такое, что для любых двух точек 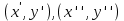 из из 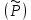 , для которых , для которых 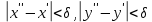 , оказывается , оказывается 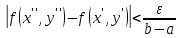 . .Положим 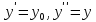 , где , где  - любое, но такое, что - любое, но такое, что 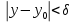 , ,  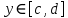 , , 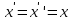 , где , где 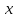 - любое из - любое из 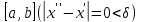 . Тогда . Тогда 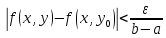 для любого для любого 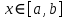 , если , если 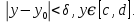 Имеем:  Итак, любому 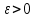 отвечает отвечает 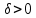 такое, что как только такое, что как только 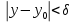 , , 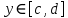 , так сейчас же , так сейчас же 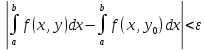 . Последнее означает, что . Последнее означает, что 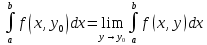 . .Совершенно аналогично доказывается утверждение: Если 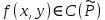 и если и если 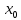 - любое из - любое из 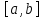 , то , то 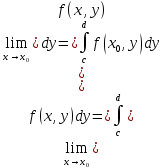 Несобственные интегралы зависящие от параметра Определение равномерной сходимости несобственных интегралов Пусть функция 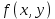 задана в области задана в области 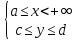 . Пусть при каждом закрепленном . Пусть при каждом закрепленном  из из  несобственный интеграл несобственный интеграл 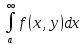 сходится. Тогда сходится. Тогда 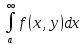 будет представлять собою функцию переменной (параметра) будет представлять собою функцию переменной (параметра) 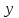 , определенную в промежутке , определенную в промежутке  (в дальнейшем будем обозначать эту функцию через (в дальнейшем будем обозначать эту функцию через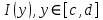 ). ).Утверждение, что несобственный интеграл 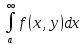 сходится при каждом сходится при каждом  из из  , означает следующее: при каждом закрепленном , означает следующее: при каждом закрепленном  из из 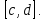 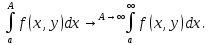 Следовательно, 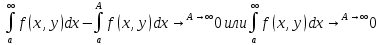 А это означает, что для каждого  из из  по любому по любому 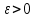 можно указать число можно указать число 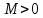 такое, что как только такое, что как только 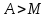 , так же , так же 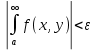 . .Важно заметить, что число 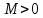 выбирается по выбирается по 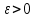 , и для каждого , и для каждого  из из  оно будет своим, то есть оно будет своим, то есть 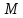 зависит от зависит от 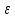 и от и от  ( ( . .Если для любого 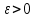 можно указать число можно указать число 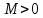 , зависящее только от , зависящее только от 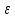 (то есть одно и то же для всех (то есть одно и то же для всех  из из  ), такое что как только ), такое что как только  , то , то  для всех для всех  из из  , то несобственный интеграл , то несобственный интеграл  называется равномерно сходящимся относительно параметра называется равномерно сходящимся относительно параметра  на на  . .Совершенно аналогично вводится понятие равномерной сходимости несобственных интегралов второго рода. Например, пусть функция  определена в области определена в области  ( ( 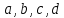 конечные числа). конечные числа).Пусть при каждом  из из  несобственный интеграл несобственный интеграл 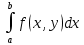 сходится. Ясно, что тогда сходится. Ясно, что тогда 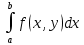 будет представлять собой функцию переменной (параметра) будет представлять собой функцию переменной (параметра)  , определенную в промежутке , определенную в промежутке  . .Утверждение, что несобственный интеграл 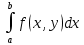 сходится при каждом сходится при каждом  из из  , означает следующее. При каждом закрепленном , означает следующее. При каждом закрепленном  из из   (  ). То есть для каждого ). То есть для каждого  из из  по любому по любому  можно указать число можно указать число  такое, что как только такое, что как только  , так сейчас же , так сейчас же  . .И здесь важно отметить, что число  выбирается по выбирается по  , и для каждого , и для каждого  из из  оно будет своим, т.е. оно будет своим, т.е.  зависит и от зависит и от  , и от , и от  . .Если же для любого  можно указать число можно указать число  , зависящее только от , зависящее только от  , такое, что как только , такое, что как только  то сейчас же то сейчас же  сразу для всех сразу для всех  из из  , то несобственный интеграл , то несобственный интеграл  называется равномерно сходящимся относительно параметра называется равномерно сходящимся относительно параметра  на на  . .О непрерывности интеграла как функции параметра Теорема: Пусть 1) функция  непрерывна в области непрерывна в области 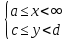 , ,2) 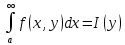 сходится равномерно относительно сходится равномерно относительно  на на  . .Тогда функция  непрерывна на непрерывна на  . .Доказательство. Возьмем любое 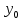 из из  и запишем его. Возьмем любое и запишем его. Возьмем любое 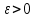 . .По условию 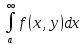 сходится равномерно относительно сходится равномерно относительно  на на  , поэтому , поэтому 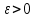 отвечает число отвечает число 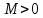 , зависящее только от , зависящее только от 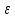 , такое, что при всяком , такое, что при всяком 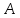 , удовлетворяющем условию , удовлетворяющем условию 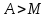 , сразу для всех , сразу для всех 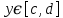 будет будет 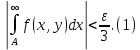 Выберем и закрепим какое-нибудь 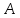 , удовлетворяющем условию , удовлетворяющем условию 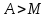 . .Положив 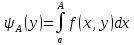 , неравенство (1) сразу для всех , неравенство (1) сразу для всех 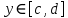 можно записать в виде: можно записать в виде: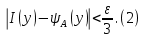  Но 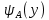 - собственный интеграл, зависящий от параметра - собственный интеграл, зависящий от параметра  . По теореме о непрерывности собственных интегралов, зависящих от параметра, заключаем, что . По теореме о непрерывности собственных интегралов, зависящих от параметра, заключаем, что 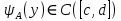 , а значит, по теореме Кантора, , а значит, по теореме Кантора, 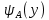 будет равномерно непрерывна на будет равномерно непрерывна на  . .Следовательно, взятому 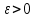 отвечает отвечает 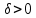 , зависящее только от , зависящее только от 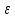 , такое, что для любых двух точек , такое, что для любых двух точек  и и 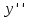 из из  , для которых , для которых 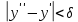 , будет , будет 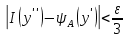 . .Для разности значений функции  в точках в точках 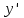 и и 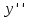 имеем: имеем: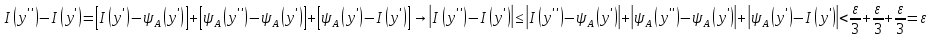 В частности, полагая 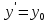 , , 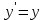 , где , где 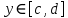 - любое, и - любое, и 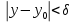 , будем иметь , будем иметь 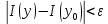 . Последнее означает, что функция . Последнее означает, что функция 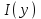 непрерывна в точке непрерывна в точке 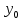 . Так как точка . Так как точка 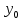 - любая из - любая из  , то заключаем, что , то заключаем, что 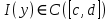 . . |
