биби. Определение интегралов зависящих от параметра
 Скачать 206.9 Kb. Скачать 206.9 Kb.
|
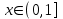 . А тогда . А тогда 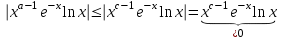 . .Так как 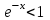 для для 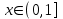 , то , то 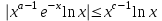 . Имеем: . Имеем: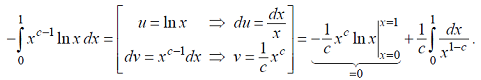 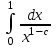 сходится, если сходится, если 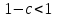 , т.е. если , т.е. если 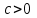 . Следовательно, по признаку равномерной сходимости несобственных интегралов, зависящих от параметра ,заключаем, что интеграл . Следовательно, по признаку равномерной сходимости несобственных интегралов, зависящих от параметра ,заключаем, что интеграл 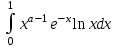 сходится равномерно относительно сходится равномерно относительно 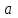 на промежутке на промежутке 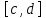 . .Рассмотрим теперь 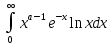 . .Для 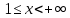 , , 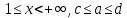 имеем: имеем: 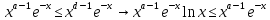 так как 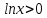 для для 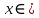 . Имеем: . Имеем: 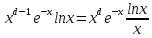 . Так как . Так как 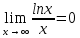 , то существует точка , то существует точка 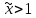 такая, что для такая, что для 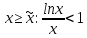 и, следовательно, для и, следовательно, для 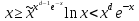 . Так как . Так как 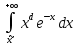 сходится при любом конечном сходится при любом конечном 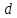 , то сходится интеграл , то сходится интеграл 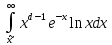 , а значит, сходится , а значит, сходится 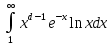 . А тогда по признаку равномерной сходимости несобственных интегралов, зависящих от параметра, заключаем, что . А тогда по признаку равномерной сходимости несобственных интегралов, зависящих от параметра, заключаем, что 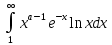 сходится равномерно относительно сходится равномерно относительно 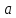 на промежутке на промежутке  . Таким образом, окончательно приходим к выводу, что интеграл . Таким образом, окончательно приходим к выводу, что интеграл 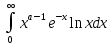 сходится равномерно относительно сходится равномерно относительно 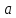 на промежутке на промежутке  . .Значит, 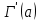 существует для любого существует для любого 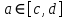 , в частности, существует , в частности, существует 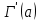 . Так как точка . Так как точка 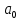 - любая ( - любая (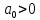 ), то заключаем: ), то заключаем: 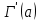 существует для существует для 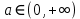 , причем , причем 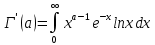 . Формула (7) доказана. . Формула (7) доказана.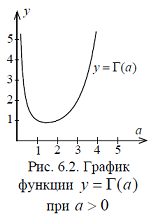 Доказательство равенства (6) проводится с помощью аналогичных оценок по индукции. Имеем 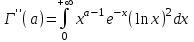 . Ясно, что . Ясно, что 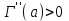 и поэтому и поэтому 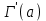 строго возрастает в строго возрастает в 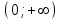 . . Так как 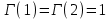 , то по теореме Роля в интервале , то по теореме Роля в интервале 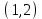 лежит точка лежит точка 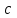 такая, что такая, что 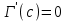 . Следовательно, . Следовательно, 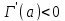 при при 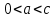 и и 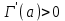 при при 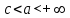 . Значит, сама функция . Значит, сама функция 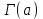 строго убывает в интервале строго убывает в интервале 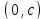 и строго возрастает в интервале и строго возрастает в интервале 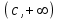 . При этом . При этом 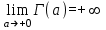 и и 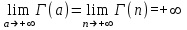 . В точке . В точке 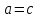 функция функция 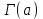 достигает своего наименьшего значения. Можно показать, что достигает своего наименьшего значения. Можно показать, что 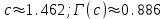 . График Гамма-функции представлен на рис….. . График Гамма-функции представлен на рис…..Замечание 1. Пользуясь основным свойством (2) Гамма-функции и опираясь на определение (1) этой функции при положительных значениях аргумента 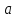 , можно определить Гамма-функцию и для отрицательных значений аргумента. В самом деле, запишем формулу (2) в виде , можно определить Гамма-функцию и для отрицательных значений аргумента. В самом деле, запишем формулу (2) в виде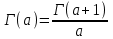 (8) (8)Из (8) видим, что зная значения Гамма-функции при каком-нибудь значении аргумента, можно вычислить ее значение при аргументе, уменьшенном на единицу. Для этого нужно прежнее значение функции разделить на уменьшенное значение аргумента. Если взять 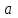 , удовлетворяющее неравенствам , удовлетворяющее неравенствам 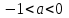 , то в правой части (8) , то в правой части (8) 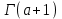 будет функцией от положительного аргумента, значение которой определено формулой (1), а в левой части (8) будет функцией от положительного аргумента, значение которой определено формулой (1), а в левой части (8)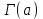 будет функцией от отрицательного аргумента. За значение будет функцией от отрицательного аргумента. За значение 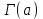 при при 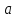 из промежутка из промежутка 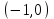 принимаем значение принимаем значение 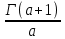 в соответствии с формулой (8). Так, например, в соответствии с формулой (8). Так, например, 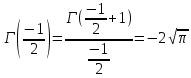 Если теперь взять 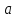 , удовлетворяющее неравенствам , удовлетворяющее неравенствам 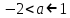 , то правая часть формулы (8) будет содержать значение Гамма-функции при аргументах из промежутка , то правая часть формулы (8) будет содержать значение Гамма-функции при аргументах из промежутка 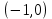 , уже определенные нами выше. Это дает возможность по формуле (8) определить значения , уже определенные нами выше. Это дает возможность по формуле (8) определить значения 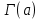 при при 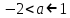 . В силу этого определения будем иметь, например: . В силу этого определения будем иметь, например: 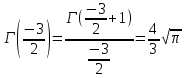 Определив теперь значения Гамма-функции в промежутке ( 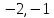 ), пользуясь формулой (8), сможем определить ее значения в промежутке ), пользуясь формулой (8), сможем определить ее значения в промежутке 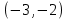 , и т.д. Так можно определить значения Гамма-функции при любых отрицательных не целых значениях аргумента , и т.д. Так можно определить значения Гамма-функции при любых отрицательных не целых значениях аргумента 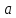 . .Выше было отмечено, что 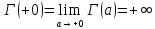 . Из формулы (8) находим, что . Из формулы (8) находим, что 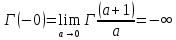 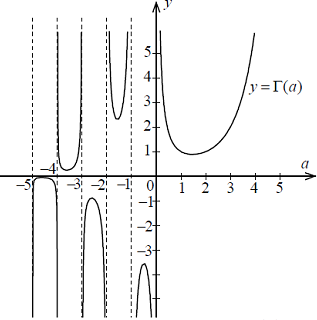 Рис.2. Пользуясь этой же формулой (8), находим, что 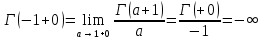 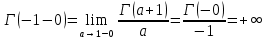 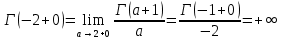 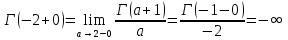 И т.д. Обычно это выражают словами так: Гамма-функция при нуле и при целых отрицательных значениях аргумента обращается в бесконечность (см рисунок). Замечание2. Введенная в этом параграфе неэлементарная функция 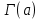 играет в математике важную роль. Для функции играет в математике важную роль. Для функции 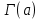 составлены подробные таблицы, и при вычислениях она может использоваться наравне с простейшими элементарными функциями – показательной, тригонометрическими и т.д. составлены подробные таблицы, и при вычислениях она может использоваться наравне с простейшими элементарными функциями – показательной, тригонометрическими и т.д.Оказывается, что определенные интегралы различных типов могут быть выражены через Гамма-функцию. В частности, к таким интегралам нередко приводят задачи, связанные с вычислением площадей и объемов. Даже если функция имеет первообразную, являющуюся элементарной функцией, интеграл от этой функции зачастую целесообразно вычислять, используя Гамма-функцию. Примеры решения Эйлеровых интегралов 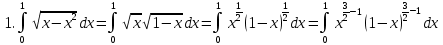 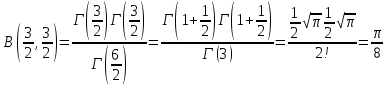 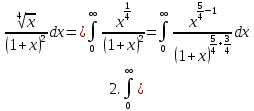 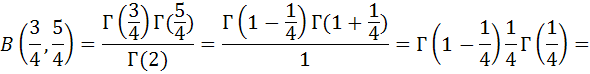 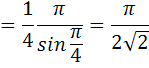 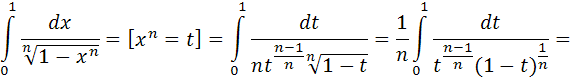 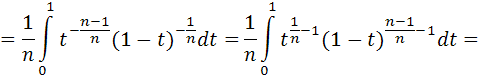 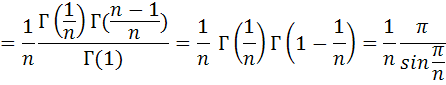 Определить область существования и выразить через эйлеровы интегралы следующие интегралы: 2.1 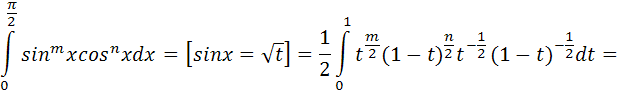 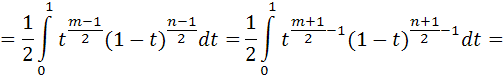 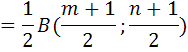 Область существования Бета-функции: 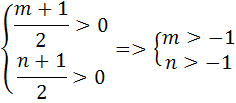 2.2 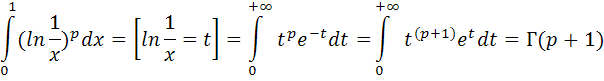 2.3 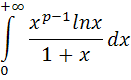 Бета-функция непрерывна в области определения и обладает частными производными любого порядка, которые можно найти путем дифференцирования по переменным x и у под знаком интеграла. 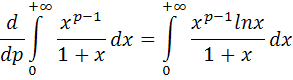 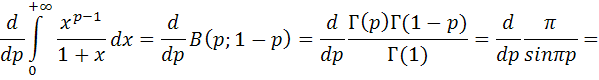 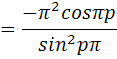 Список литературы Канторович, Л.В. Функциональный анализ / Л.В. Канторович, Г.П. Акилов. - СПб.: BHV, 2004. - 816 c. Канторович, Л.В. Функциональный анализ / Л.В. Канторович. - СПб.: BHV, 2004. - 816 c. Князев, П.Н. Функциональный анализ / П.Н. Князев. - М.: КД Либроком, 2009. - 208 c. Корпусов, М.О. Нелинейный функциональный анализ и математическое моделирование в физике: Методы исследования нелинейных операторов / М.О. Корпусов, А.Г. Свешников. - М.: Красанд, 2011. - 480 c. Корпусов, М.О. Нелинейный функциональный анализ и математическое моделирование в физике: Геометрические и топологические свойства линейных пространств / М.О. Корпусов, А.Г. Свешников. - М.: Красанд, 2011. - 416 c. Лебедев, В.И. Функциональный анализ и вычислительная математика / В.И. Лебедев. - М.: Физматлит, 2005. - 296 c. Луговая, Г.Д. Функциональный анализ: специальные курсы / Г.Д. Луговая. - М.: ЛКИ, 2013. - 256 c. Луговая, Г.Д. Функциональный анализ: Специальные курсы / Г.Д. Луговая, А.Н. Шерстнев. - М.: ЛКИ, 2013. - 256 c. Луговая, Г.Д. Функциональный анализ: Специальные курсы / Г.Д. Луговая, А.Н. Шерстнев. - М.: Ленанд, 2019. - 256 c. Миротин, А.Р. Функциональный анализ: Мера и интеграл / А.Р. Миротин. - М.: КД Либроком, 2013. - 160 c. Миротин, А.Р. Функциональный анализ: Мера и интеграл. / А.Р. Миротин. - М.: КД Либроком, 2013. - 160 c. Свешников, А.Г. Нелинейный функциональный анализ и его приложения к уравнениям в частных производных / А.Г. Свешников, А.Б. Альшин, М.О. Корпусов. - М.: Научный мир, 2008. - 400 c. Сканави, А.А. Функциональный анализ. Лекции и упражнения (для бакалавров) / А.А. Сканави. - М.: КноРус, 2013. - 464 c. Треногин, В.А. Функциональный анализ: Учебник / В.А. Треногин. - М.: Физматлит, 2007. - 488 c. Треногин, В.А. Функциональный анализ: Учебное пособие / В.А. Треногин. - М.: Academia, 2017. - 128 c. Треногин, В.А. Функциональный анализ: учебное пособие. в 2 т. Т. 2 / В.А. Треногин. - М.: Academia, 2018. - 288 c. Треногин, В.А. Функциональный анализ: в 2 т.Т. 2: Учебное пособие / В.А. Треногин. - М.: Академия, 2019. - 320 c. Треногин, В.А. Функциональный анализ / В.А. Треногин. - М.: Физматлит, 2004. - 488 c. Хелемский, А.Я. Квантовый функциональный анализ в бескоординатном изложении / А.Я. Хелемский. - М.: МЦНМО, 2009. - 304 c. Шамин, Р.В. Функциональный анализ от нуля до единицы / Р.В. Шамин. - М.: Ленанд, 2016. - 272 c. Шерстнев, А.Н. Математический и функциональный анализ: Конспект лекций / А.Н. Шерстнев. - М.: Ленанд, 2018. - 376 c. |
